线性SVM决策过程可视化

绘制思路：

1. 获取数据集的横纵坐标最大值及最小值（xlim，ylim）
2. 将横纵坐标轴平均分为n份（axisx，axisy）
3. 通过meshgrid函数进行广播，生成网格点（xy）
4. 通过SVC.decision_function方法计算网格内每个点到决策边界的距离
5. 通过contour函数绘制决策边界及虚线超平面

1.导入我们需要的模块

from sklearn.datasets import make_blobs
from sklearn.svm import SVC
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

2.创建数据集，查看分布情况

#创建数据集并可视化
X,y = make_blobs(n_samples = 50,centers=2,random_state=0,cluster_std=0.6)
plt.scatter(X[:,0],X[:,1],c = y,cmap = 'gist_rainbow')
plt.xticks([])
plt.yticks([])
#隐藏x，y坐标轴

3.理解contour函数

$matplotlib.axes.Axes.contour([X,Y,]Z,[levels],\ast \ast kwargs)$

Contour是专门用来绘制等高线的函数。等高线，本质上是在二维图像上表现三维图像的一种形式，其中两维X和Y是两条坐标轴上的取值，而Z表示高度。Contour就是将由X和Y构成平面上的所有点中，高度一致的点连接成线段的函数，在同一条等高线上的点一定具有相同的Z值。我们可以利用这个性质来绘制我们的决策边界。

参数	含义
$X，Y$	选填。二维平面上所有的点的横纵坐标取值，一般要求是二维结构并且形状需要与Z相同，往往通过numpy.meshgrid()这样的函数来创建。如果X和Y都是一维，则Z的结构必须为(len(Y), len(X))。如果不填写，则默认X = range(Z.shape[1])，Y = range(Z.shape[0])。
$Z$	必填。平面上所有的点所对应的高度。
$levels$	可不填，不填默认显示所有的等高线，填写用于确定等高线的数量和位置。如果填写整数n，则显示n个数据区间，即绘制n+1条等高线。水平高度自动选择。如果填写的是数组或列表，则在指定的高度级别绘制等高线。列表或数组中的值必须按递增顺序排列。

4.画决策边界：制作网格，理解函数meshgrid

#先有散点图
plt.scatter(X[:,0],X[:,1],c = y,cmap = 'gist_rainbow')
#获取散点图的坐标轴
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()
#在最大值和最小值之间取30个数
axisx = np.linspace(xlim[0],xlim[1],30)
axisy = np.linspace(ylim[0],ylim[1],30)
#进行广播，生成矩阵
axisx,axisy = np.meshgrid(axisx,axisy)
#组合后生成平面上的900个点
xy = np.vstack([axisx.ravel(),axisy.ravel()]).T

看一下meshgrid生成的矩阵网格：

#看一下生成的点的矩阵（网格）
plt.scatter(xy[:,0],xy[:,1],cmap = 'rainbow',s = 0.1)

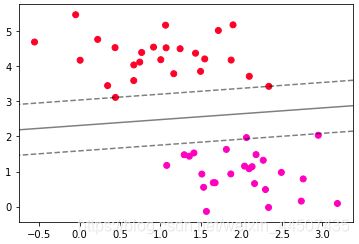
5.绘制决策边界

#先有散点图
plt.scatter(X[:,0],X[:,1],c = y,cmap = 'gist_rainbow')
#获取散点图的坐标轴
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()

#建模，计算决策边界并找出网格上每个点到决策边界的距离
clf = SVC(kernel = 'linear').fit(X,y)
#decision_function返回每个输入样本到决策边界的距离
#然后再将这个距离转换为axisx的结构，
#这是由于画图的函数contour要求Z的结构必须与X和Y保持一致
z = clf.decision_function(xy).reshape(axisx.shape)

ax.contour(axisx,axisy,z
          ,colors = 'k'
          ,levels = [-1,0,1]
          ,alpha = 0.5
          ,linestyles = ['--','-','--']
          )
ax.set_xlim(xlim)
ax.set_ylim(ylim)

6.将上述过程包装为函数

#将上述过程包装成函数
def plot_svc_decision_function(model,ax=None):
    if ax == None:
        ax = plt.gca()
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()
    
    axisx = np.linspace(xlim[0],xlim[1],30)
    axisy = np.linspace(ylim[0],ylim[1],30)
    
    axisx,axisy = np.meshgrid(axisx,axisy)
    xy = np.vstack([axisx.ravel(),axisy.ravel()]).T
    
    Z = model.decision_function(xy).reshape(axisx.shape)
    
    ax.contour(axisx,axisy,Z
              ,colors = 'k'
              ,levels = [-1,0,1]
              ,linestyles = ['--','-','--']
              )
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

plt.scatter(X[:,0],X[:,1],cmap = 'rainbow',c=y)
clf = SVC(kernel = 'linear').fit(X,y)
plot_svc_decision_function(clf)

也可以绘制非线性数据集的决策边界：

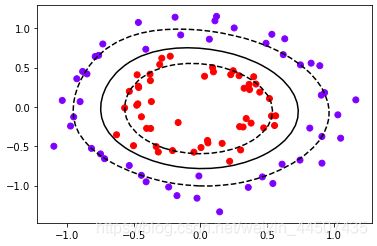
#推广到非线性情况（环形数据集为例）
from sklearn.datasets import make_circles

X,y = make_circles(n_samples = 100,factor = 0.5,noise = 0.1,random_state=0)
#factor ：外圈与内圈的尺度因子<1
plt.scatter(X[:,0],X[:,1],c = y ,cmap = 'rainbow')

#尝试用定义好的函数划分决策边界
clf = SVC(kernel = 'rbf').fit(X,y)
plot_svc_decision_function(clf)