学习笔记 Graph Neural Network (李宏毅 机器学习)

Graph Neural Networks

Introduction

How to embed node into a feature space using convolution?

• Solution 1: Generalize the concept of convolution (correlation) to graph >> Spatial-based convolution

• Solution 2: Back to the definition of convolution in signal processing >> Spectral-based convolution

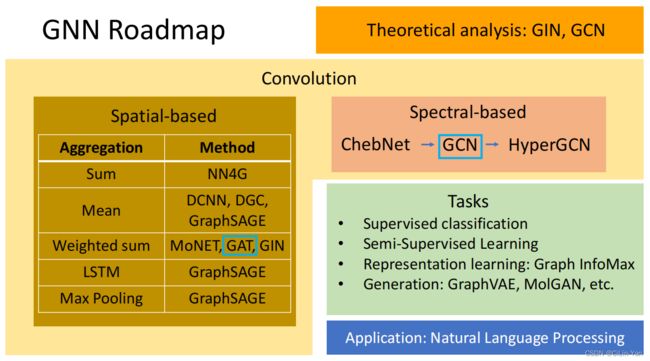
Roadmap

Tasks, Dataset

Tasks

• Semi-supervised node classification
• Regression
• Graph classification
• Graph representation learning
• Link prediction

Common dataset

• CORA: citation network. 2.7k nodes and 5.4k links
• TU-MUTAG: 188 molecules with 18 nodes on average

Spatial-based GNN

Terminology:

• Aggregate: 用 neighbor feature update 下一層的 hidden state.
• Readout: 把所有 nodes 的 feature 集合起來代表整個 graph.

NN4G (Neural Networks for Graph)

Aggregate 使用 sum.

Readout 对每一个 hidden layer 的 mean of nodes’ feature 做 weighted sum 得到 prediction.

DCNN (Diffusion-Convolution Neural Network )

Aggregate 使用 mean

Readout 对每一个 hidden layer 的 nodes’ feature 做concatenate 得到一个 matrix, 对这个matrix 做 concatenate 之后与 weighted 相乘得到 prediction.

DGC (Diffusion Graph Convolution)

Readout 的时候对每个 hidden layer 的 matrix 做 add 而不是 concatenate.

MoNET (Mixture Model Networks)

• Define a measure on node ‘distances’

• Use weighted sum (mean) instead of simply summing up (averaging) neighbor features.

$$h_3^1=w\left({\hat{u}}_{3,0}\right)\times h_0^0+w\left({\hat{u}}_{3,2}\right)\times h_2^0+w\left({\hat{u}}_{3,2}\right)\times h_4^0$$

$w(\cdot )$ is a NN, $\hat{u}$ is a transform from $u$, where $\mathbf{u}(x,y)={\left(\frac{1}{\sqrt{\mathrm{deg}(\mathrm{x})}},\frac{1}{\sqrt{\mathrm{deg}(\mathrm{y})}}\right)}^{\top }$

GraphSAGE

• SAmple and aggreGatE

• Can work on both transductive and inductive setting

• GraphSAGE learns how to embed node features from neighbors

• AGGREGATION: mean, max-pooling, or LSTM

GAT (Graph Attention Networks)

$✓$ Input: node features $\mathbf{h}=\left\{h_1,h_2,\dots ,h_N\right\},h_i\in {\mathbb{R}}^F$ :
$✓$ Calculate energy: $e_{ij}=a\left(\mathbf{W}{h}_i,\mathbf{W}{h}_j\right)$
$✓$ Attention score (over the neighbors)
$${\alpha }_{ij}=\frac{\exp \left(\mathrm{LeakyReLU}\left({\mathbf{a}}^T\left[\mathbf{W}{h}_i\Vert \mathbf{W}{h}_j\right]\right)\right)}{{\sum }_{k\in {\mathcal{N}}_i}\exp \left(\mathrm{LeakyReLU}\left({\mathbf{a}}^T\left[\mathbf{W}{h}_i\Vert \mathbf{W}{h}_k\right]\right)\right)}$$

GIN (Graph Isomorphism Network)

• A GNN can be at most as powerful as WL isomorphic test

• Theoretical proofs were provided

• $h_v^{(k)}={\mathrm{MLP}}^{(k)}\left(\left(1+{ϵ}^{(k)}\right)\cdot h_v^{(k-1)}+{\sum }_{u\in \mathcal{N}(v)}{h}_u^{(k-1)}\right)$

• Sum instead of mean or max 使用 sum 比 mean 和 max 好

• MLP instead of 1-layer

Graph Signal Processing and Spectral-based GNN

Spectral Graph Theory

$✓$ Graph: $G=(V,E),N=|V|$

$✓A\in {\mathbb{R}}^{N\times N}$, adjacency matrix (weight matrix).
$$A_{i,j}=0\text{ if }{e}_{i,j}\notin E\text{, else }{A}_{i,j}=w(i,j)$$
$✓$ We only consider undirected graph

$✓D\in {\mathbb{R}}^{N\times N}$, degree matrix
$$D_{i,j}=\{\begin{array}{ll}d(i)& \text{ if }i=j\text{ (Sum of row }i\text{ in }A\text{ ) }\\ 0& \text{ if }i\ne j\end{array}$$
$✓f:V\to {\mathbb{R}}^N$, signal on graph (vertices). $f(i)$ denotes the signal onvertex $i$

$✓$ Graph Laplacian $L=D-A,L⩾0$ (Positive semidefinite)

$✓L$ is symmetric (for undirected graph)

$✓L=U\Lambda U^{\mathrm{T}}$ (spectral decomposition)

$✓\Lambda =\mathrm{diag}\left({\lambda }_0,\dots ,{\lambda }_{N-1}\right)\in {\mathbb{R}}^{N\times N}$

$✓U=\left[u_0,\dots ,u_{N-1}\right]\in {\mathbb{R}}^{N\times N}$, orthonormal

$✓{\lambda }_l$ is the frequency, $u_l$ is the basis corresponding to ${\lambda }_l$

图卷积： $y=g_{\theta }(L)x$

Lemma 3 Let $G$ be a weighted graph, and $\mathcal{L}$ the graph Laplacian of $G$. Fix an integer $s>0$, and pick vertices $m$ and $n$. Then ${\left({\mathcal{L}}^s\right)}_{m,n}=0$ whenever $d_G(m,n)>s.$

ChebNet

Use polynomial to parametrize ${\mathrm{g}}_{\theta }(L)$
$$g_{\theta }(L)=\sum _{k=0}^K{\theta }_k{L}^k$$
$✓$ Now it is K-localized

$✓$ Parameters to be learnt: $O(K)$
Problem: Time complexity: $O\left(N^2\right)$ Use a polynomial function that can be computed recursively from $L$

$✓$ Chebyshev polynomial
$$T_0(x)=1,T_1(x)=x,T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x),x\in [-1,1]$$

Define $\Lambda =\frac{2\Lambda }{{\lambda }_{\max }}-\mathrm{I},\tilde{\lambda }\in [-1,1]$, we have:

$$T_0(\Lambda )=\mathrm{I},T_1(\Lambda )=\Lambda ,T_k(\Lambda )=2\Lambda T_{k-1}(\Lambda )-T_{k-2}(\Lambda )$$

and then,

$$\begin{array}{rl}y=g_{{\theta }^{\prime }}(L)x& =\sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\tilde{L})x\\ & ={\theta }_0^{\prime }{T}_0(L)x+{\theta }_1^{\prime }{T}_1(L)x+{\theta }_2^{\prime }{T}_2(L)x+\cdots +{\theta }_K^{\prime }{T}_K(L)x\\ & ={\theta }_0^{\prime }{\bar{x}}_0+{\theta }_1^{\prime }{\bar{x}}_1+{\theta }_2^{\prime }{\bar{x}}_2+\cdots +{\theta }_K^{\prime }{\bar{x}}_K\\ & =\left[\begin{array}{llll}{\bar{x}}_0& {\bar{x}}_1& \dots & {\bar{x}}_K\end{array}\right]\left[\begin{array}{lll}{\theta }_0^{\prime }& {\theta }_1^{\prime }& \dots {\theta }_K^{\prime }\end{array}\right]\end{array}$$
where ${\bar{x}}_0=x,{\bar{x}}_1=\tilde{L}x,{\bar{x}}_k=2\tilde{L}{\bar{x}}_{k-1}-{\bar{x}}_{k-2}$

Calculating ${\bar{x}}_k=2\tilde{L}{\bar{x}}_{k-1}-{\bar{x}}_{k-2}$ cost $O(E)$, Total complexity: $O(KE)$.

GCN

$$\begin{array}{rl}y=g_{{\theta }^{\prime }}(L)x& =\sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\tilde{L})x,K=1\\ y=g_{{\theta }^{\prime }}(L)x& ={\theta }_0^{\prime }x+{\theta }_1^{\prime }\tilde{L}x\\ & ={\theta }_0^{\prime }x+{\theta }_1^{\prime }\left(\frac{2\mathrm{L}}{{\lambda }_{\max }}-\mathrm{I}\right)x\\ & ={\theta }_0^{\prime }x+{\theta }_1^{\prime }(L-\mathrm{I})x\\ & ={\theta }_0^{\prime }x-{\theta }_1^{\prime }\left(D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x\\ & =\theta \left(I+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\right)x\end{array}$$

where $\tilde{\mathrm{L}}=\frac{2\mathrm{L}}{{\lambda }_{\max }}-\mathrm{I}$, ${\lambda }_{\max }\approx 2$, $L=I-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}$, $\theta ={\theta }_0^{\prime }=-{\theta }_1^{\prime }$

renormalization trick: $I_N+D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}\to {\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$
$$H^{(l+1)}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)}\right)$$
Can be rewritten as: (conclusion)
$$h_v=f\left(\frac{1}{|\mathcal{N}(v)|}\sum _{u\in \mathcal{N}(v)}W{x}_u+b\right),\forall v\in \mathcal{V}$$

Discussion

$✓$ For any initial value $X^{(0)}$, the output of l-th layer $X^{(l)}$ satisfies $d_{\mathcal{M}}\left(X^{(l)}\right)\le$ $(s\lambda {)}^l{d}_{\mathcal{M}}\left(X^{(0)}\right)$. In particular, $d_{\mathcal{M}}\left(X^{(l)}\right)$ exponentially converges to 0 when $s\lambda <1$. 所以，如果$s\lambda <1$，多层的MLP表现不如浅层的MLP.

$✓$ In reality, graph is usually not too sparse, so GCN is still applicable

$✓$ Find the sweet-spot to make the singular value of the weight not too small and not too big

$✓$ Remedy for over-smoothing: sample edges while training to make the graph sparser

$✓$ DropEdge Randomly drop the edge of input graph with probability $p$, 可上避免 over-smoothing 的問題

• 每一層都用同一個 drop 過的 adjacency matrix
• 每一層都用不同的 drop 過的 adjacency matrix

Online Resources

$✓$ PyG (PyTorch Geometric) is a library built upon PyTorch to easily write and train Graph Neural Networks (GNNs) for a wide range of applications related to structured data.

$✓$ DEEP GRAPH LIBRARY

Summary and Take Home Notes

$✓$ GAT and GCN are the most popular GNNs
$✓$ Although GCN is mathematically driven, we tend to ignore its math
$✓$ GNN (or GCN) suffers from information lose while getting deeper
$✓$ Many deep learning models can be slightly modified and designed to fit graph data, such as Deep Graph InfoMax, Graph Transformer, GraphBert.
$✓$ Theoretical analysis must be dealt with in the future
$✓$ GNN can be applied to a variety of tasks

Reference

博文所有内容摘抄自 Hung-yi Lee 机器学习, 国内可访问 Bilibili 搬运视频，课件可见 GNN.