蓝桥杯第十三届国赛PythonB组题解

蓝桥杯第十三届国赛PythonB组题解

【写在前边】

这次的题还是比较难的，只做出来7道，交上去6道，还有一半是暴力做的。只求国三了

开局两道填空题用了快两个小时，直接搞崩了心态。。淦！

本题解仅代表个人观点及思路，不代表标准答案。欢迎各位巨佬指导交流。

所有代码均存放于仓库：

Github：https://github.com/AYO-YO/Algorithm/tree/蓝桥杯_国赛

Gitee: https://gitee.com/ayo_yo/Algorithm/tree/蓝桥杯_国赛

试题A：斐波那契与7（5分）

【问题描述】
斐波那契数列的递推公式为：$F_n=F_{n-1}+F_{n-2}$，其中$F_1=F_2=1$。
请问，斐波那契数列的第$1$至$202202011200$项（含）中，有多少项的个位是$7$。

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

【思路分析】

这道题又是一个超大数，斐波那契本来就是指数级增长，直接爆肯定是不行的。

经过两位大佬@m0_62944359的勘误，原方法是错误的。

同时由评论区大佬@秋雨洗鸡肉提醒，斐波那契数列的个位数60个为1轮，直接1000内的数+100内的数是不对的，会导致部分数错误计算。

因此在此写出大佬@秋雨洗鸡肉的正确方法：

• 斐波那契数列个位数60个为一个循环

• 60个数中共有8个7。

  1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1 0
  1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1 0
  1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1 0
  1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1 0
  1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1 0
  1 1 2 3 5 8 3 1 4 5 9 4 3 7 0 7 7 4 1 5 6 1 7 8 5 3 8 1 9 0 9 9 8 7 5 2 7 9 6 5 1 6 7 3 0 3 3 6 9 5 4 9 3 2 5 7 2 9 1 0
  

• 因此，最终结果应为：

  202202011200/60
  Out[3]: 3370033520.0
  _*8
  Out[4]: 26960268160.0
  

【参考答案】

    26960268160

【完整代码】

A.py (Gitee.com) A.py (github.com)

试题B: 小蓝做实验（5分）

【问题描述】
小蓝很喜欢科研，他最近做了一个实验得到了一批实验数据，一共是两百万个正整数。如果按照预期，所有的实验数据 x 都应该满足 10⁷ ≤ x ≤ 10⁸。但是做实验都会有一些误差，会导致出现一些预期外的数据，这种误差数据 y 的范围是 10³
≤ y ≤ 10¹² 。由于小蓝做实验很可靠，所以他所有的实验数据中 99.99% 以上都是符合预期的。小蓝的所有实验数据都在 primes.txt 中，现在他想统计这两百万个正整数中有多少个是质数，你能告诉他吗？

【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

---

【思路分析】

这个题有200w个数，直接暴力找肯定不行。我一开始走了弯路子，多线程，素数判断优化都用上了。最后才发现我想多了，比赛结束前1分钟才把数爆出来，也没时间写针对大数的素性测试了。。思路如下：

1. 首先观察数据，均以1、3、5、7结尾。大于1000且结尾为5的数，肯定能被5整除，于是先利用编辑器正则替换所有以5结尾的数，此时剩下约150w多个数：

   \d+?5
   
   

2. 使用埃氏筛选法，获得10^8以内的所有质数，这里注意，利用埃氏筛选法需要进行优化，不然也是跑的头大。我在之前博客里也写过直接判断质数的优化方法，除了2、3，所有质数均位于6n左右。因此可以直接将埃氏筛选法的步长拉到6，这样速度能进一步提升，然后影响埃氏筛选法速度的大头主要是2、3、5，需要进行多次循环才能筛掉后边的合数，因此预处理在生成列表时直接将2、3、5的倍数归0。理论上直接归零的质数倍数越多，生成素数就越快。

   计数质数 Python 埃氏筛选法_AYO_YO的博客-CSDN博客

   判断质数 Python Java C++_AYO_YO的博客-CSDN博客

   def getprimes(n):
       ls = [i if i % 2 != 0 and i % 3 != 0 and i % 5 != 0 else 0 for i in range(n + 1)]
       ls[1], ls[2], ls[3], ls[5] = 0, 2, 3, 5
       for i in range(6, n + 1, 6):
           f = i - 1
           if f != 0:
               for j in range(2 * f, n + 1, f):
                   ls[j] = 0
               continue
           f = i + 1
           if f != 0:
               for j in range(2 * f, n + 1, f):
                   ls[j] = 0
       return filter(lambda x: x != 0, ls)
   

3. 埃氏筛选法筛选$10^8$以内的质数大概需要2分钟左右，再大恐怕就难以承受了。于是先将$10^8$的质数统计出来，并把大于$10^8$的质数拎出来。得到结果$10^8$以内的质数有506733个。大数有约130个。

   506733
   [542693491967, 142787902577, 452440529173, 663634895869, 71242929179, 999870483413, 441673697183, 895134836909, 59008094959, 812048153483, 153230177243, 5986461211, 825268545161, 85386152959, 305669636917, 176618331487, 627185459239, 517233054923, 347714268719, 75380450897, 652349118967, 746710276723, 887316078643, 55623754253, 726602124691, 63723051253, 11944000489, 14326008041, 995344474081, 127374806651, 101228446879, 782792370337, 7616731547, 672817895497, 309261587441, 993510068537, 898280626321, 691250724803, 436362423451, 135244424501, 873959450791, 404517752423, 803431472291, 890481756773, 299729772337, 993254812121, 939705423281, 928689411767, 950796808643, 925182899009, 867933942403, 177084914339, 374154056921, 195931411013, 636268614181, 845966263637, 669349089677, 279219681547, 116772294307, 458677064359, 414099720659, 553029935971, 225122592047, 523383194647, 291752440213, 29190046721, 756126896941, 400963923179, 807339716593, 666619632839, 792597812483, 157223341237, 515677221383, 869902952023, 277744493561, 279840195947, 12066121523, 659914745389, 796743912131, 973038777059, 856703807231, 66169702601, 987064845247, 916671221021, 884623305749, 504935549881, 232438712231, 701919604183, 542037833447, 521942095081, 726449610001, 840499018589, 492469281101, 757165962919, 437417377471, 903288533789, 254110134101, 265121359891, 776841707227, 854559132599, 325401328397, 675731682791, 730947154187, 280786162939, 670729451441, 48996391291, 286681507897, 847973529401, 166381727761, 568868879153, 56085663143, 417414542761, 666771906149, 857635614683, 188918440631, 490214446741, 82741563491, 411523187461, 304024439243, 912661149107, 556591023551, 934801057481, 828742723319, 814141769183, 528476615281, 560425065263, 224638484077, 610321268093, 655599334577, 624348698849]
   

4. 这些大数直接判断是否是质数也是相当恐怖的，于是判断特大数是否是质数，就要用另一个方法——费马素性测试。这个是我之前算法课期末作业研究过的一个算法，就是利用随机数随机对大数取余，如果能整除，就不是质数；加入了一个优化，加入了一个互质判断，大大提升了算法效率以及准确率。

   for p in bigNum:
       K = 100 # 取随机数验证的次数，该次数越大，准确率越高。实测K=10就能得到准确结果了
       k = 0
       while k < K:  # 这里用while是后续判定随机完成率是否是100%
           b = int(random.random() * (p - 1) + 1)  # 生成一个1~p-1之间的随机整数
           factor = math.gcd(b, p)  # 计算b,p的最大公约数
           r = runFermatPower(b, p, p)  # 计算b^p mod p
           print(f"第{k + 1}次取随机数, 随机数b={b}, {b}和{p}的最大公约数为{factor}, r=({b}^{p})mod p={r}", end=', ')
           if factor > 1:
               print(f"因b={b}与p={p}的最大公约数为{factor}，不为互质数，故p={p}为合数")
               break
           elif r != b:
               print(f"因r={r},({b}^{p}) mod p ={r}!={b}, 故p={p}为合数")
               break
           else:
               print(f"故p={p}可能为素数")
               k += 1
       if k == K:
           print(f"经过{K}次循环验证, p={p}可能为素数, n为素数的概率为{(1 - 1 / (2 ** k)) * 100}%")
   

5. 得到最终结果：

   506753
   

【完整代码】

比赛过程中的代码是分步骤的，一步步写，然后得到结果后再计算下一步，这个代码是优化过的完整版代码，直接运行就能得到最终结果。

B.py (Gitee.com) B.py (github.com)

试题C：取模（10分，10s，512MB）

【问题描述】

给定$n,m$，问是否存在两个不同的数$x,y$使得$1\le x<y\le m$且$n$mod$x$=$n$mod$y$。

【输入格式】

输入包含多组独立的询问。

第一行包含一个整数 T 表示询问的组数。

接下来$T$行每行包含两个整数$n,m$，用一个空格分隔，表示一组询问。

【输出格式】

输出$T$行，每行依次对应一组询问的结果。如果存在，输出单词 Yes；如果不存在，输出单词 No。

【样例输入】

3
1 2
5 2
999 99

【样例输出】

No 
No 
Yes

【评测用例规模与约定】

对于$20\%$的评测用例，$T\le 100，n,m\le 1000$；

对于$50\%$的评测用例，$T\le 10000，n,m\le 10^5$；

对于所有评测用例，$1\le T\le 10^5，1\le n\le 10^9，2\le m\le 10^9$。

---

【思路分析】

没啥巧妙的解法，直接暴力做，通关估计够呛。

【参考代码】

C.py (Gitee.com) C.py (github.com)

试题D：内存空间（10分，10s，512MB）

【问题描述】

小蓝最近总喜欢计算自己的代码中定义的变量占用了多少内存空间。为了简化问题，变量的类型只有以下三种：

int：整型变量，一个 int 型变量占用 4 Byte 的内存空间。

long：长整型变量，一个 long 型变量占用 8 Byte 的内存空间。

String：字符串变量，占用空间和字符串长度有关，设字符串长度为 L，则字符串占用 L Byte 的内存空间，如果字符串长度为 0 则占用 0 Byte 的内存空间。

定义变量的语句只有两种形式，第一种形式为：

type var1=value1,var2=value2…;

定义了若干个 type 类型变量 var1、var2、…，并且用 value1、value2…初始化，多个变量之间用, 分隔，语句以; 结尾，type 可能是 int、long 或 String。例如 int a=1,b=5,c=6; 占用空间为 12 Byte；long a=1,b=5;占用空间为 16 Byte；String s1=””,s2=”hello”,s3=”world”;
占用空间为 10 Byte。

第二种形式为：

type[] arr1=new type[size1],arr2=new type[size2]…;

定义了若干 type 类型的一维数组变量 arr1、arr2…，且数组的大小为 size1、size2…，多个变量之间用, 进行分隔，语句以; 结尾，type 只可能是 int 或 long。例如 int[] a1=new int[10]; 占用的内存空间为 40 Byte；long[] a1=new long[10],a2=new long[10]; 占用的内存空间为160 Byte。

已知小蓝有 T 条定义变量的语句，请你帮他统计下一共占用了多少内存空间。结果的表示方式为：aGBbMBcKBdB，其中 a、b、c、d 为统计的结果，GB、MB、KB、B 为单位。优先用大的单位来表示，1GB=1024MB， 1MB=1024KB，1KB=1024B，其中 B 表示 Byte。如果 a、b、c、d 中的某几个数字为0，那么不必输出这几个数字及其单位。题目保证一行中只有一句定义变量的语句，且每条语句都满足题干中描述的定义格式，所有的变量名都是合法的且均不重复。题目中的数据很规整，和上述给出的例子类似，除了类型后面有一个空格，以及定义数组时 new 后面的一个空格之外，不会出现多余的空格。

【输入格式】

输入的第一行包含一个整数$T$，表示有$T$句变量定义的语句。接下来$T$行，每行包含一句变量定义语句。

【输出格式】

输出一行包含一个字符串，表示所有语句所占用空间的总大小。

【样例输入 1】

1

long[] nums=new long[131072];

【样例输出 1】

1MB

【样例输入 2】

4
int a=0,b=0; long x=0,y=0;
String s1=”hello”,s2=”world”;
long[] arr1=new long[100000],arr2=new long[100000];

【样例输出 2】

1MB538KB546B

【样例说明】

样例 1，占用的空间为$131072\times 8=1048576B$，换算过后正好是 1MB，其它三个单位 GB、KB、B 前面的数字都为 0 ，所以不用输出。

样例 2，占用的空间为$4\times 2+8\times 2+10+8\times 100000\times 2B$，换算后是1MB538KB546B。

【评测用例规模与约定】

对于所有评测用例，$1\le T\le 10$，每条变量定义语句的长度不会超过$1000$。所有的变量名称长度不会超过$10$，且都由小写字母和数字组成。对于整型变量，初始化的值均是在其表示范围内的十进制整数，初始化的值不会是变量。对于 String 类型的变量，初始化的内容长度不会超过$50$，且内容仅包含小写字母和数字，初始化的值不会是变量。对于数组类型变量，数组的长度为一个整数，范围为：$[0,2^{30}]$，数组的长度不会是变量。$T$条语句定义的变量所占的内存空间总大小不会超过 1 GB，且大于 0 B。

【思路分析】

这个题乍一看还挺唬人的，占了足足3页，因为我前两道填空题占用了非常多的时间，已经开始慌了，到这题时一看题，心想凉了，这才第二道编程题就这么难了吗但仔细读了一下题目，发现并不难，跟着题目做就行，得益于Python操作字符串非常方便，所以能给这道题省下不少功夫。

思路如下：

• 首先应该计算当前表达式占用了多少Byte，而且表达式中变量名、=、关键字new这些都属于无关变量，直接忽略即可

• 获取输入的单行表达式后，使用input().split(maxsplit=1)获取输入并以第一个空格分隔，主要是用于判断最左侧的数据类型if '[]' in typ

• 如果类型为数组，注意数组只有int和long：

  • 获取数组的类型以后，直接正则匹配赋值式中的中括号（初始化数组的长度信息在这里，例如int[] arr = new int[3];取3）乘以对应变量长度相加即可

• 如果类型为普通类型，则需要额外判断是不是String：

  • 若为String：直接正则”.+?”匹配”，注意题目样例里这是一个中文字符。匹配到所有值以后直接计算长度相加即可。
  • 若不为String：直接.count(',')计算,的长度，变量数量比,数量多1，然后乘以对应长度相加即可。

• 把总长度按要求格式输出即可：

  def convertSize(byte):
      size = {'GB': 0, 'MB': 0, 'KB': 0, 'B': 0}
      if byte >= 1073741824:
          size['GB'] = byte // 1073741824
      byte %= 1073741824
      if byte >= 1048576:
          size['MB'] = byte // 1048576
      byte %= 1048576
      if byte >= 1024:
          size['KB'] = byte // 1024
      byte %= 1024
      size['B'] = byte
      return size
  
  
  def printSize(l):
      size = convertSize(l)
      ans = ''
      # 正常情况下直接遍历字典即可，但我不太确定考试环境的3.8中的字典是否有序。3.9以后肯定是有序的了
      if size['GB'] > 0:
          ans += f'{size["GB"]}GB'
      if size['MB'] > 0:
          ans += f'{size["MB"]}MB'
      if size['KB'] > 0:
          ans += f'{size["KB"]}KB'
      if size['B'] > 0:
          ans += f'{size["B"]}B'
      print(ans)
  

【参考代码】

D.py (Gitee.com) D.py (github.com)

试题E：近似GCD（15分，10s，512MB）

【问题描述】

小蓝有一个长度为$n$的数组$A=(a_1,a_2,\cdot \cdot \cdot ,a_n)$，数组的子数组被定义为从原数组中选出连续的一个或多个元素组成的数组。数组的最大公约数指的是数组中所有元素的最大公约数。如果最多更改数组中的一个元素之后，数组的最大公约数为 g，那么称 g 为这个数组的近似 GCD。一个数组的近似 GCD
可能有多种取值。

具体的，判断 g 是否为一个子数组的近似 GCD 如下：

1. 如果这个子数组的最大公约数就是 g，那么说明 g 是其近似 GCD。
2. 在修改这个子数组中的一个元素之后（可以改成想要的任何值），子数组的最大公约数为 g，那么说明 g 是这个子数组的近似 GCD。

小蓝想知道，数组 A 有多少个长度大于等于 2 的子数组满足近似 GCD 的值为 g。

【输入格式】

输入的第一行包含两个整数 n, g，用一个空格分隔，分别表示数组 A 的长度和 g 的值。

第二行包含 n 个整数$a_1,a_2,\cdot \cdot \cdot ,a_n$，相邻两个整数之间用一个空格分隔。

【输出格式】

输出一行包含一个整数表示数组 A 有多少个长度大于等于 2 的子数组的近似 GCD 的值为 g 。

【样例输入】

5 3
1 3 6 4 10

【样例输出】

5

【样例说明】

满足条件的子数组有 5 个：

$[1,3]$：将 1 修改为 3 后，这个子数组的最大公约数为 3 ，满足条件。

$[1,3,6]$：将 1 修改为 3 后，这个子数组的最大公约数为 3 ，满足条件。

$[3,6]$：这个子数组的最大公约数就是 3 ，满足条件。

$[3,6,4]$：将 4 修改为 3 后，这个子数组的最大公约数为 3 ，满足条件。

$[6,4]$：将 4 修改为 3 后，这个子数组的最大公约数为 3，满足条件。

【评测用例规模与约定】

对于$20\%$的评测用例，$2\le n\le 10^2$；

对于$40\%$的评测用例，$2\le n\le 10^3$；

对于所有评测用例，$2\le n\le 10^5，1\le g,a_i\le 10^9$。

---

【思路分析】

这道题虽然说是gcd，但和gcd其实没有什么关系。。。

主要是划分子数组，如果子数组中只有至多 1 个数不是 g 的因子。那么这个子数组就是满足条件的，因为可以任意修改，无需关注修改为什么值。

【参考代码】

E.py (Gitee.com) E.py (github.com)

试题I：owo（25分，10s，512MB）

【问题描述】

小蓝很喜欢 owo ，他现在有一些字符串，他想将这些字符串拼接起来，使得最终得到的字符串中出现尽可能多的 owo 。

在计算数量时，允许字符重叠，即 owowo 计算为 2 个，owowowo 计算为3 个。

请算出最优情况下得到的字符串中有多少个 owo。

【输入格式】

输入的第一行包含一个整数 n ，表示小蓝拥有的字符串的数量。接下来 n 行，每行包含一个由小写英文字母组成的字符串 si 。

【输出格式】

输出 n 行，每行包含一个整数，表示前 i 个字符串在最优拼接方案中可以得到的 owo 的数量。

【样例输入】

3
owo w ow

【样例输出】

1
1
2

【评测用例规模与约定】

对于$10\%$的评测用例，$n\le 10$；

对于$40\%$的评测用例，$n\le 300$；

对于$60\%$的评测用例，$n\le 5000$；

对于所有评测用例，$1\le n\le 10^6，1\le |s_i|，|s_i|\le 10^6$，其中$|s_i|$表示字符串$s_i$的长度。

---

【思路分析】

这个题虽然是25分的题，但用Python来做，不算难，，盲猜应该用动规，但时间不多了，来不及细推，我选择的是直接暴力做。暴力全排列，时间复杂度极其之高。虽然题目给了10s，，但估计还是过不去。

• 首先是找到字符串里的owo，这个比较取巧的方法就是直接正则'owo'匹配，但是正则一个字符只能匹配一次，但是题目要求中o可以用两次，那么直接.replace('o','oo')，把每个o
  扩充成两个，这样就可以正常进行正则匹配了。
• 将每次输入都保存到数组中，然后使用itertools.permutations()生成全排列，再循环寻找最大owo最多的数组。

【完整代码】

I.py (Gitee.com) I.py (github.com)

试题J：替换字符（25分，10s，512MB）

【问题描述】

给定一个仅含小写英文字母的字符串 s，每次操作选择一个区间$[l_i,r_i]$将 s的该区间中的所有字母$x_i$全部替换成字母$y_i$，问所有操作做完后，得到的字符串是什么。

【输入格式】

输入的第一行包含一个字符串 s 。第二行包含一个整数 m 。

接下来 m 行，每行包含 4 个参数$l_i,r_i,x_i,y_i$，相邻两个参数之间用一个空格分隔，其中$l_i,r_i$为整数，$x_i,y_i$为小写字母。

【输出格式】

输出一行包含一个字符串表示答案。

【样例输入】

abcaaea 4
1 7 c e
3 3 e b
3 6 b e
1 4 a c

【样例输出】

cbecaea

【评测用例规模与约定】

对于$40\%$的评测用例，$|s|,m\le 5000$；

对于所有评测用例，$1\le |s|,m\le 10^5，1\le l_i\le r_i\le |s|，x_i\ne y_i$，其中 |s| 表示字符串 s 的长度。

---

【思路分析】

这个题甚至比之前的更简单，觉得需要优化吧，一看时间给了10s。直接跟着题目淦就行了。

【完整代码】

J.py (Gitee.com) J.py (github.com)

———分割线———

做出来的到这儿就结束了，剩下的三道题没做出来，恳请赐教哇。

试题F：交通信号（15分，10s，512MB）

【问题描述】
LQ 市的交通系统可以看成由 n 个结点和 m 条有向边组成的有向图。在每条边上有一个信号灯，会不断按绿黄红黄绿黄红黄… 的顺序循环 (初始时刚好变到绿灯)
。当信号灯为绿灯时允许正向通行，红灯时允许反向通行，黄灯时不允许通行。每条边上的信号灯的三种颜色的持续时长都互相独立，其中黄灯的持续时长等同于走完路径的耗时。当走到一条边上时，需要观察边上的信号灯，如果允许通行则可以通过此边，在通行过程中不再受信号灯的影响；否则需要等待，直到允许通行。

请问从结点 s 到结点 t 所需的最短时间是多少，如果 s 无法到达 t 则输出−1。

【输入格式】

输入的第一行包含四个整数$n,m,s,t$，相邻两个整数之间用一个空格分隔。接下来 m 行，每行包含五个整数$u_i,v_i,g_i,r_i,d_i$
，相邻两个整数之间用一个空格分隔，分别表示一条边的起点，终点，绿灯、红灯的持续时长和距离（黄灯的持续时长）。

【输出格式】

输出一行包含一个整数表示从结点 s 到达 t 所需的最短时间。

【样例输入】

4 4 1 4
1 2 1 2 6
4 2 1 1 5
1 3 1 1 1
3 4 1 99 1

【样例输出】

11

【评测用例规模与约定】

对于 40% 的评测用例，$n\le 500，1\le g_i,r_i,d_i\le 100$；

对于 70% 的评测用例，$n\le 5000$；

对于所有评测用例，$1\le n\le 100000，1\le m\le 200000，1\le s,t\le n，1\le u_i,v_i\le n，1\le g_i,r_i,d_i\le 10^9$。

---

【思路分析】

emmm，这个题说实话，题都有点没读明白。。

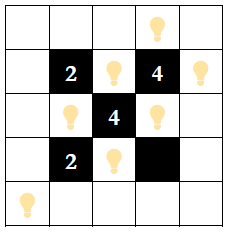
试题G：点亮（20分，10s，512MB）

【问题描述】

小蓝最近迷上了一款名为《点亮》的谜题游戏，游戏在一个 n × n
的格子棋盘上进行，棋盘由黑色和白色两种格子组成，玩家在白色格子上放置灯泡，确保任意两个灯泡不会相互照射，直到整个棋盘上的白色格子都被点亮（每个谜题均为唯一解）。灯泡只会往水平和垂直方向发射光线，照亮整行和整列，除非它的光线被黑色格子挡住。黑色格子上可能有从
0 到 4 的整数数字，表示与其上下左右四个相邻的白色格子共有几个灯泡；也可能没有数字，这表示可以在上下左右四个相邻的白色格子处任意选择几个位置放置灯泡。游戏的目标是选择合适的位置放置灯泡，使得整个棋盘上的白色格子都被照亮。

例如，有一个黑色格子处数字为 4，这表示它周围必须有 4 个灯泡，需要在他的上、下、左、右处分别放置一个灯泡；如果一个黑色格子处数字为 2，它的上下左右相邻格子只有 3
个格子是白色格子，那么需要从这三个白色格子中选择两个来放置灯泡；如果一个黑色格子没有标记数字，且其上下左右相邻格子全是白色格子，那么可以从这 4 个白色格子中任选出 0 至 4 个来放置灯泡。

题目保证给出的数据是合法的，黑色格子周围一定有位置可以放下对应数量的灯泡。且保证所有谜题的解都是唯一的。

现在，给出一个初始的棋盘局面，请在上面放置好灯泡，使得整个棋盘上的白色格子被点亮。

【输入格式】

输入的第一行包含一个整数 n，表示棋盘的大小。

接下来 n 行，每行包含 n 个字符，表示给定的棋盘。字符 . 表示对应的格子为白色，数字字符 0、1、2、3、4 表示一个有数字标识的黑色格子，大写字母 X 表示没有数字标识的黑色格子。

【输出格式】

输出 n 行，每行包含 n 个字符，表示答案。大写字母 O 表示对应的格子包含灯泡，其它字符的意义与输入相同。

【样例输入】

5
.....
.2.4.
..4..
.2.X.
.....

【样例输出】

...O.
.2O4O
.O4O.
.2OX. 
O....

【样例说明】

答案对应的棋盘布局如下图所示：

【评测用例规模与约定】

对于所有评测用例，$2\le n\le 5$，且棋盘上至少有$15$的格子是黑色格子。

---

【思路分析】

深搜？动规？？不会，，要不是时间太紧，差点写爆破

试题H：打折（20分，15s，512MB）

【问题描述】

小蓝打算采购 n 种物品，每种物品各需要 1 个。

小蓝所住的位置附近一共有 m 个店铺，每个店铺都出售着各种各样的物品。

第 i 家店铺会在第$s_i$天至第$t_i$天打折，折扣率为$p_i$，对于原件为 b 的物品，折后价格为$\lfloor \frac{b\cdot p_j}{100}\rfloor$。其它时间需按原价购买。

小蓝很忙，他只能选择一天的时间去采购这些物品。请问，他最少需要花多少钱才能买到需要的所有物品。

题目保证小蓝一定能买到需要的所有物品。

【输入格式】

输入的第一行包含两个整数 n, m，用一个空格分隔，分别表示物品的个数和店铺的个数。

接下来依次包含每个店铺的描述。每个店铺由若干行组成，其中第一行包含四个整数$s_i,t_i,p_i,c_i$，相邻两个整数之间用一个空格分隔，分别表示商店优惠的起始和结束时间、折扣率以及商店内的商品总数。之后接$c_i$
行，每行包含两个整数$a_j,b_j$，用一个空格分隔，分别表示该商店的第 j 个商品的类型和价格。商品的类型由 1 至 n 编号。

【输出格式】

输出一行包含一个整数表示小蓝需要花费的最少的钱数。

【样例输入】

2 2
1 2 89 1
1 97
3 4 77 1
2 15

【样例输出】

101

【评测用例规模与约定】

对于 40% 的评测用例，$n,m\le 500，s_i\le t_i\le 100，c_i\le 2000$；

对于 70% 的评测用例，$n,m\le 5000，c_i\le 20000$；

对于所有评测用例，$1\le n,m\le 100000，1\le ci\le n，ci\le 400000，1\le s_i\le t_i\le 10^9，1<p_i<100，1\le a_j\le n，1\le b_j\le 10^9$。

---

【思路分析】

又是一道看题目都费劲的题，，不过盲猜应该类似于背包问题。