列生成算法求解矩形下料问题（Matlab代码）

深切哀悼抗击新冠肺炎疫情斗争牺牲烈士和逝世同胞

这学期接了《运筹学》课程，在国内抗疫的大环境下，勉勉强强当了七周主播，刚刚讲完对偶理论。

这里必须要吐槽一下《线性代数》的老师，本科生的课程不要放水好不好？讲单纯形法足足用了三周课，每堂课都要给学生科普或者强化线代基础。

为了强化学生对对偶理论的理解，计划在接下来三周课程里介绍大规模问题的优化方法，Dantzig-Wolfe分解，Benders分解和ADMM（Alternating direction method of multipliers）。
（想想后面还要讲整数规划、动态规划、网络规划、非线性规划、排队论、……，头都大。）

说到Dantzig-Wolfe分解，不得不提的就是列生成算法，最早用来解决一维下料问题（cutting stock problem）。但一维下料问题似乎太乏味了，怕学生们提不起兴趣，这里就找了一篇解决矩形下料问题的文章，复现了一下。

Cintra G F , Miyazawa F K , Wakabayashi Y , et al. Algorithms for two-dimensional cutting stock and strip packing problems using dynamic programming and column generation[J]. European Journal of Operational Research, 2008, 191(1):61-85.
https://doi.org/10.1016/j.ejor.2007.08.007

同行们一定都很熟悉这篇文章，很好的解决了gcut中13个算例，并且提出了变尺寸母板的解决策略。

这里只实现了最基本的几段代码。

Matlab代码

// 生成离散点集
function P=DPP(D,d)
P=0;
m = length(d);
for j=0:D
    c(j+1)=0;
end
for i=1:m
    for j=d(i):D
        if c(j+1)<c(j-d(i)+1)+d(i)
            c(j+1)=c(j-d(i)+1)+d(i);
        end
    end
end
mind = min(d);
for j=1:D-mind
    if c(j+1)==j
        P=[P,j];
    end
end
P=[P,D];

// 矩形背包问题算法
// 为方便回溯方案，将item修改为三维整数矩阵，前两维对应状态空间，第三维为该状态空间最大价值时满足各订单的数量 
// guillotine 改为整数二维数组，其中0 ———— 不切；1 ———— 对w方向切割；2 ———— 对h方向切割
function [z,V,item,guillotine,position]=DP(W,H,w,h,v)
m=length(w);
P=DPP(W,w);
Q=DPP(H,h);
r=length(P);
s=length(Q);
V=zeros(r,s);
item=zeros(r,s,m);
guillotine=zeros(r,s);
position=zeros(r,s);
for i=1:r
    for j=1:s
        [V(i,j),item(i,j,:)]=inital_dp(w,h,v,P,Q,i,j); //调用第三段程序初始化状态空间
        guillotine(i,j)=0;
    end
end
for i=2:r
    for j=2:s
        [~,n]=max(P(P<=floor(P(i)/2)));
        for x=1:n
            [~,t]=max(P(P<=(P(i)-P(x))));
            if V(i,j)<V(x,j)+V(t,j)
                V(i,j)=V(x,j)+V(t,j);
                item(i,j,:)=item(x,j,:)+item(t,j,:);
                position(i,j)=P(x);
                guillotine(i,j)=1;  %w方向切割
            end
        end
        [~,n]=max(Q(Q<=floor(Q(j)/2)));
        for y=1:n
            [~,t]=max(Q(Q<=(Q(j)-Q(y))));
            if V(i,j)<V(i,y)+V(i,t)
                V(i,j)=V(i,y)+V(i,t);
                item(i,j,:)=item(i,y,:)+item(i,t,:);
                position(i,j)=Q(y);
                guillotine(i,j)=2;  %h方向切割
            end
        end
    end
end
z=zeros(m,1);
for i=1:m
    z(i)=item(r,s,i);
end

// 初始化每个状态空间的最大价值
function [V,maxk]=inital_dp(w,h,v,P,Q,i,j)
V=0;
m=length(v);
maxk=zeros(1,m);
for k=1:m
    if w(k)>P(i)
        continue;
    end
    if h(k)>Q(j)
        continue;
    end
    if v(k)>V
        V=v(k);
        maxk=zeros(1,m);
        maxk(k)=1;
    end
end

//列生成算法主程序
//用"\","/"替代 *inv()
//绘图时用 cut(i).w cut(i).h 存储第i个待画任务对应状态空间的横纵编号 cut.x cut.y 存储其起始位置（左下坐标值）
//方案结果呈现（绘图）的回溯算法暂时没想到更好的方法，欢迎大家提供宝贵意见！
function [B,ans]=SimplexCG(filename)
file = [.\gcut\',filename,'.txt'];  //算例存放在下级gcut文件夹中
data = textread(file);
m=data(1,1);
W=data(2,1);
H=data(2,2);
w=data(3:2+m,1)';
h=data(3:2+m,2)';
d=data(3:2+m,3)';
x=d;
B=eye(m);
P=DPP(W,w);
Q=DPP(H,h);
r=length(P);
s=length(Q);
m_V=zeros(m,r,s);
m_item=zeros(m,r,s,m);
m_guil=zeros(m,r,s);
m_pos=zeros(m,r,s);
while(true)
    y=ones(1,m)/B;
    [z,V,item,guillotine,position]=DP(W,H,w,h,y);
    if y*z<=1
        break;
    end
    omega=inv(B)*z;
    t=1e6;
    s=-1;
    for j=1:m
        if omega(j)<=0
            continue;
        end
        if t>(x(j)/omega(j))
            t=x(j)/omega(j);
            s=j;
        end
    end
    if s==-1
        break;
    end
    m_V(s,:,:)=V;
    m_item(s,:,:,:)=item;
    m_guil(s,:,:)=guillotine;
    m_pos(s,:,:)=position;
    for i=1:m
        B(i,s)=z(i);
        if i==s
            x(i)=t;
        else
            x(i)=x(i)-omega(i)*t;
        end
    end
end
ans = x;
P=DPP(W,w);
Q=DPP(H,h);
r=length(P);
s=length(Q);
//画出最后方案
for i=1:m
    figure(i);
    hold on
    plot([0,W,W],[H,H,0])
    cut(1).w=r;
    cut(1).h=s;
    cut(1).x=0;
    cut(1).y=0;
    while(~isempty(cut))
        a=cut(1).w;
        b=cut(1).h;
        x=cut(1).x;
        y=cut(1).y;
        cut(1)=[];
        num=length(cut);
        if m_guil(i,a,b)==0
            continue;
        end
        if m_guil(i,a,b)==1
            plot([x+m_pos(i,a,b),x+m_pos(i,a,b)],[y,y+Q(b)]);
            [~,cut(num+1).w]=max(P(P<=m_pos(i,a,b)));
            cut(num+1).h=b;
            cut(num+1).x=x;
            cut(num+1).y=y;
            [~,cut(num+2).w]=max(P(P<=P(a)-m_pos(i,a,b)));
            cut(num+2).h=b;
            cut(num+2).x=x+m_pos(i,a,b);
            cut(num+2).y=y;
        end
        if m_guil(i,a,b)==2
            plot([x,x+P(a)],[y+m_pos(i,a,b),y+m_pos(i,a,b)]);
            cut(num+1).w=a;
            [~,cut(num+1).h]=max(Q(Q<=m_pos(i,a,b)));
            cut(num+1).x=x;
            cut(num+1).y=y;
            cut(num+2).w=a;
            [~,cut(num+2).h]=max(Q(Q<=Q(b)-m_pos(i,a,b)));
            cut(num+2).x=x;
            cut(num+2).y=y+m_pos(i,a,b);
        end
    end
end 

算例文件

格式参考gcut设置，具体如下：

1. 第一行数据 ‘5’ 表示订单种类数；
2. 第二行数据’300 500’表示母板规格（宽300 x 长500）；
3. 第三行起为订单数据 ‘40 60 2300’ 表示 宽40长60的订单需求为2300件。

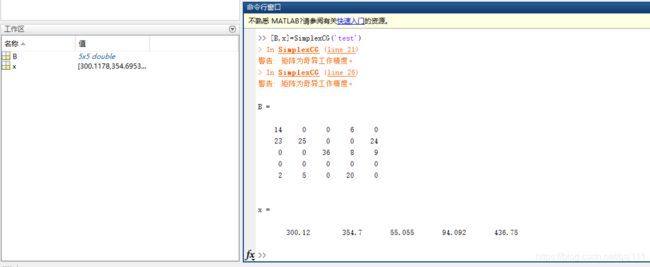
运行结果

1. B为算法结束时基矩阵；
2. x为最优解，每列方案使用次数。

最优解方案展示

推荐大家关注公众号数据魔术师。