java column_干货 | 10分钟带你彻底了解column generation（列生成）算法的原理附java代码...

OUTLINE

前言

预备知识预警

什么是column generation

相关概念科普

Cutting Stock Problem

CG求解Cutting Stock Problem

列生成代码

reference

00 前言

这几天勤奋的小编一直在精确算法的快乐学习之中不能自拔。到列生成算法这一块，看了好几天总算把这块硬骨头给啃下来了。然后发现网上关于列生成的教学资料也不是很多，大部分讲的不是那么通俗易懂。所以今天就打算写一写这个算法，尽可能写得通俗易懂。

01 预备知识预警

由于列生成算法涉及的知识点非常多，所以在开始之前希望读者必须要具备以下的基础知识，不然就没法往下玩了：

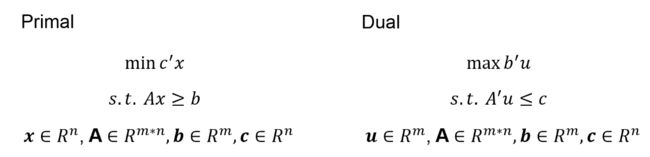
线性规划以及线性规划对偶问题

单纯形法原理

原问题的影子价格(shadow price)以及对偶变量

单纯形法非基变量进基时非基变量检验数(reduce cost)的计算

以上内容我就不展开科普了。如果对这些概念还有不熟悉的小伙伴，一定要回去搞清楚再往下看哦。

02 什么是column generation？

2.1 相关背景

Column generation 是一种用于求解大规模线性优化问题的非常高效的算法。[3]其理论基础是由Danzig等于1960年提出。本质上而言，列生成算法就是单纯形法的一种形式，是用来求解线性规划问题的。列生成算法已被应用于求解如下著名的NP-hard优化问题：机组人员调度问题(Crew Assignment Problem)、切割问题(Cutting Stock Problem)、车辆路径问题(Vehicle Routing Problem)、单资源工厂选址问题(The single facility location problem )等。

2.2 larger linear programs

在某些线性优化问题的模型中,约束的数目有限，但是变量的数目随着问题规模的增长会爆炸式的增长，因此不能把所有的变量都显性的在模型中表达出来。比如下面一个线性规划问题：

\[min (y_1 +...+y_n) \\

R1: a_{11}y_1+...+a_{1n}y_n \ge 10 \\

R2: a_{21}y_1+...+a_{2n}y_n \ge 40 \\

R3: a_{31}y_1+...+a_{3n}y_n \ge 80 \\

\]

从中可以看出，约束条件只有三个，但是当n=10000时，其变量数就达到了10000个。这类问题就是大规模的线性优化问题了。

2.3 column generation

单纯型法虽然能保证在数次迭代后找到最优解，但是其面对变量很多的线性规划问题就显得很弱了。因为它需要去在众多变量里进行基变换，就上面的问题而言，你想想你要在近10000个变量里面找个能进基的，活着不好吗？

再有，在用单纯形法求解这类线性规划问题时，基变量(basic variable)只与约束的个数相关，每次迭代只会有一个新的非基变量(non-basic variable)进基，因此，在整个求解过程中其实只有很少一部分变量会被涉及到。

因此，有人基于单纯型法提出了列生成算法。其思路大概如下：[1]

先把原问题(master problem)restrict到一个规模更小(即变量数比原问题少的)的restricted master problem，在restricted master problem上用单纯型法求最优解，但是此时求得的最优解只是restricted master problem上的，并不是master problem的最优解。

此时，就需要通过一个subproblem去check在那些未被考虑的变量中是否有使得reduced cost小于零的？如果有，那么就把这个变量的相关系数列加入到restricted master problem的系数矩阵中，回到第1步。

经过反复的迭代，直到subproblem中的reduced cost rate大于等于零，那么master problem就求到了最优解。

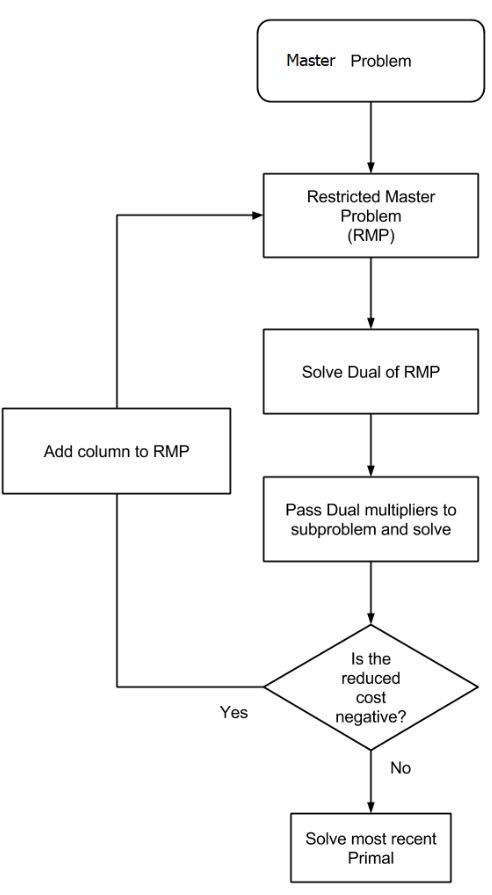
看算法流程图会更加直观哦：[2]

03 相关概念科普

刚刚讲的内容涉及到了几个概念，master problem，restricted master problem，subproblem等，这一节来把这几个概念给讲清楚。基于一个问题线性规划问题：

\[min (y_1 +...+y_n) \\

R_1: a_{11}y_1+...+a_{1n}y_n \ge b_1\\

R_2: a_{21}y_1+...+a_{2n}y_n \ge b_2\\

…… \\

R_m: a_{m1}y_1+...+a_{mn}y_n \ge b_m\\

\]

3.1 master problem(MP)

master problem可以认为是原问题。即

\[min (y_1 +...+y_n) \\

R_1: a_{11}y_1+...+a_{1n}y_n \ge b_1\\

R_2: a_{21}y_1+...+a_{2n}y_n \ge b_2\\

…… \\

R_m: a_{m1}y_1+...+a_{mn}y_n \ge b_m\\

\]

3.2 restricted master problem(RMP)

前面我们说过，把原问题(master problem)restrict到一个规模更小(即变量数比原问题少的)的就是restricted master problem了。比如可以用启发式算法，在上面的master problem找出满足条件(也就是形成的restricted master problem必须要有可行解)的k个列，得到如下的restricted master problem：

\[min (y_1+y_2+...+y_k) \\

R_1: a_{11}y_1+...+a_{1k}y_k \ge b_1 \\

R_2: a_{21}y_1+...+a_{2k}y_k \ge b_2 \\

…… \\

R_m: a_{m1}y_1+...+a_{mk}y_k \ge b_m \\

\]

可以看到，相比原来的master problem，restricted master problem相当于把\(y_{k+1}...y_m\)强制限制为非基变量了。[4]

3.3 subproblem

核能预警，如果这部分看不懂，请确保预备知识过关。如果预备知识不过关，请在运筹学老师的陪同下观看，谢谢合作！

上面的限制主问题求解完成后，我们想使用单纯型法进行基变量的转换，看看\(y_{k+1}...y_m\)中，是否有可以转入基变量的列。还记得怎么找进基的非基变量吗？(不记得就去问你们的运筹学老师)。当然是通过非基变量的检验数辣，通过\(\sigma_j = c_j - c_BB^{-1}a_j\)，在\(y_{k+1}...y_m\)中寻找检验数最小并且为负数的变量，将变量对应的那一列添加到RMP中。

那么，在检验数的计算公式中，大家还记得\(c_BB^{-1}\)是什么吗？\(c_BB^{-1}\)有两重含义：

通过求解RMP问题得到的影子价格(shadow price)。

通过求解RMP对偶问题得到的对偶变量(dual variable)。

所以在开始之前小编一直强调预备知识一定要过关。这两个含义意味着我们有上面两种方式得到\(c_BB^{-1}\)，不过我们一般倾向于使用第二种，WHY？

虽然通过单纯型法直接求解restricted master problem能得到\(c_BB^{-1}\)。但是restricted master problem也可能是一个变量很多的线性规划。前面也说过了，单纯型法对变量很多的问题是无能为力的。因此通过单纯型法求restricted master problemde的对偶问题(将restricted master problem对偶一下，就能使得变量数大幅减小，因为这些变量转换成了对偶问题中的限制条件了)，能更快地得到子问题想要的\(c_BB^{-1}\)。[1]

所以我们总结一下：

通过求解RMP问题或者RMP对偶问题，得到我们想要的\(c_BB^{-1}\)以后，subproblem就是通过\(\sigma_j = c_j - c_BB^{-1}a_j\)这条公式，在\(y_{k+1}...y_m\)中寻找检验数为负并且最小的变量，将变量对应的那一列添加到RMP中。

3.4 算法流程图

通过上面讲了这么多以后，这里在给出一个更详细的流程图：[5]

04 Cutting Stock Problem[1]

讲column generation怎么可能少得了Cutting Stock Problem这个经典的问题呢！

我们有以下问题，原纸卷每个长为L=17m，顾客们分别需要25个3m长，20个5m长，18个7m长的纸卷。那么需要怎样切割才能使得浪费最小呢？

Master Problem

Column Generation Formulation：

\(P\)是所有可行的裁剪方案的集合，里面方案的总数为n(我们并不需要确切的知道这个值是多少，只需要知道它很大)。

\(a_{ij}\) 表示第j种方案里类别i的个数。

\(y_{j}\)表示第 j 种方案的选择个数。

于是，我们得到如下模型：

\[min (y_1 +...+y_n) \\

R1: a_{11}y_1+...+a_{1n}y_n \ge 25 \\

R2: a_{21}y_1+...+a_{2n}y_n \ge 20 \\

R3: a_{31}y_1+...+a_{3n}y_n \ge 18 \\

\]

这样，我们得到了Cutting Stock Problem的Master Problem。

05 CG求解Cutting Stock Problem

通过上面的问题分析和建模以后，我们这一步一步一步来求解该问题，让大家彻底理解column generation这个过程。该过程模拟需要用到一个线性求解器，大家还记得小编以前讲过的lpsolve的教程吗?赶紧去翻一下以前的教程，把lpsolveIDE装上，然后跟着小编的脚步一步一步往下走。

5.1 restricted master problem(RMP)

前面我们完成了问题的建模，得到了Cutting Stock Problem的Master Problem。现在，我们可以用启发式算法找到一个满足客户需要的初始解：

首先，一个卷筒有三种切割方案：

方案1：切成5个3m

方案2：切成2个6m

方案3：切成2个7m

很容易得出，5个方案1、10个方案2、8个方案3，是能满足所有客户需求的。即得到MP的一个RMP如下：

\[min (y_1 +...+y_3) \\

R1: a_{11}y_1+...+a_{13}y_3 \ge 25 \\

R2: a_{21}y_1+...+a_{23}y_3 \ge 20 \\

R3: a_{31}y_1+...+a_{33}y_3 \ge 18 \\

\]

其中，

\[a_{11} = 5,a_{12} = 0, a_{13} = 0 \\

a_{21} = 0,a_{22} = 2, a_{13} = 0 \\

a_{31} = 0,a_{32} = 0, a_{13} = 2 \\

\]

这三列分别对应着5个方案1、10个方案2、8个方案3。还有一点需要注意的，对于每一列，都需要满足：

\(3a_{1j} + 6a_{2j}+ 7a_{3j} \le 16\)，也就是每一卷纸只有16的长度，不能超出这个长度。这个叫列生成规则，不同问题有不同的规则约束。subproblem在寻找某些列或者生成某些列时，就是受到列生成规则的约束的。

5.2 开始列生成过程

iteration 1

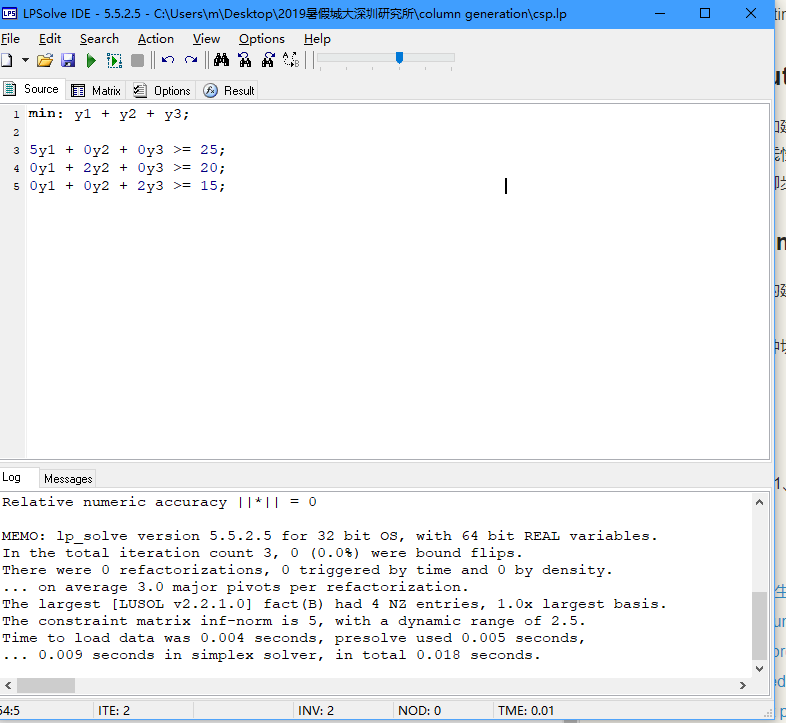
RMP：

\[min (y_1 +...+y_3) \\

R1: 5y_1+0y_2+0y_3 \ge 25 \\

R2: 0y_1+2y_2+0y_3 \ge 20 \\

R3: 0y_1+0y_2+2y_3 \ge 18 \\

\]

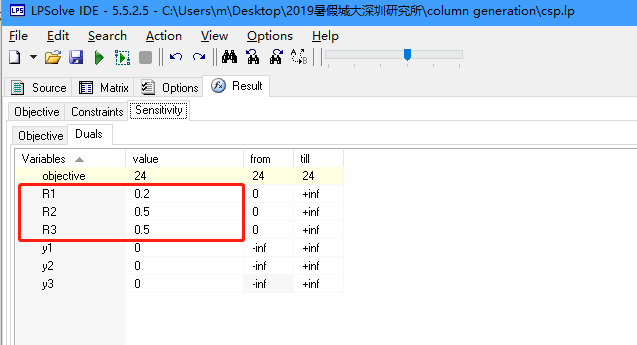
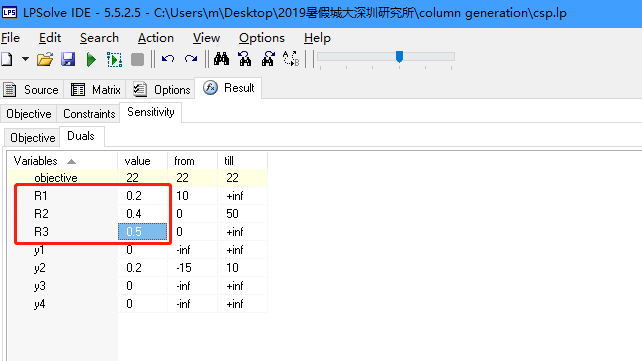
将该模型输入lpsolve，得到对偶变量如下：

得到\(c_BB^{-1} = [0.2, 0.5, 0.5]\)。现在要找一列加入RMP，是哪一列呢？现在还不知道，我们暂记为\(\alpha_4 = [a_{14},a_{24},a_{34}]^T\)。非基变量检验数\(\sigma_4 = c_4 - c_BB^{-1}\alpha_4 = 1 - 0.2a_{14}-0.5a_{24}-0.5a_{34}\)。

subproblem：

\[min (1 - 0.2a_{14}-0.5a_{24}-0.5a_{34}) \\

s.t. 3a_{14} + 6a_{24}+ 7a_{34} \le 16 \\

a_{ij} \in Z

\]

求解结果得$ \alpha_4 = [1,2,0]^T, \sigma_4= -0.2 < 0\(,reduced cost 为负数，因此将\) \alpha_4$加入RMP，开始第二轮迭代。

iteration 2

RMP：

\[min (y_1 +...+y_3+y_4) \\

R1: 5y_1+0y_2+0y_3 +1y_4\ge 25 \\

R2: 0y_1+2y_2+0y_3+2y_4 \ge 20 \\

R3: 0y_1+0y_2+2y_3+0y_3 \ge 18 \\

\]

将该模型输入lpsolve，得到对偶变量如下：

得到\(c_BB^{-1} = [0.2, 0.4, 0.5]\)。现在要找一列加入RMP，是哪一列呢？现在还不知道，我们暂记为\(\alpha_5 = [a_{15},a_{25},a_{35}]^T\)。非基变量检验数\(\sigma_5 = c_5 - c_BB^{-1}\alpha_5 = 1 - 0.2a_{15}-0.4a_{25}-0.5a_{35}\)。

subproblem：

\[min (1 - 0.2a_{15}-0.4a_{25}-0.5a_{35}) \\

s.t. 3a_{15} + 6a_{25}+ 7a_{35} \le16 \\

a_{ij} \in Z

\]

求解结果得$ \alpha_5 = [1,1,1]^T, \sigma_5= -0.1 < 0\(,reduced cost 为负数，因此将\) \alpha_5$加入RMP，开始第三轮迭代。

iteration 3

RMP：

\[min (y_1 +...+y_3+y_4+y5) \\

R1: 5y_1+0y_2+0y_3 +1y_4+1y_5\ge 25 \\

R2: 0y_1+2y_2+0y_3+2y_4+1y_5 \ge 20 \\

R3: 0y_1+0y_2+2y_3+0y_3 +1y_5\ge 18 \\

\]

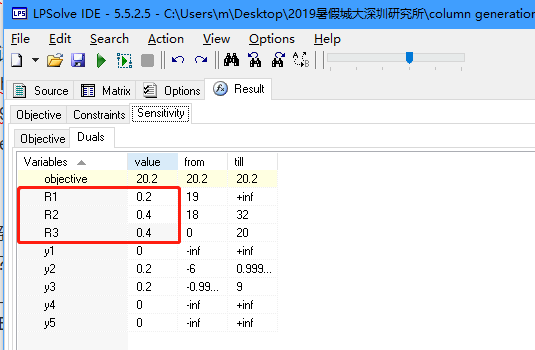
将该模型输入lpsolve，得到对偶变量如下：

得到\(c_BB^{-1} = [0.2, 0.4, 0.4]\)。现在要找一列加入RMP，是哪一列呢？现在还不知道，我们暂记为\(\alpha_6 = [a_{16},a_{26},a_{36}]^T\)。非基变量检验数\(\sigma_6 = c_6 - c_BB^{-1}\alpha_6 = 1 - 0.2a_{16}-0.4a_{26}-0.5a_{36}\)。

subproblem：

\[min (1 - 0.2a_{16}-0.4a_{26}-0.5a_{36}) \\

s.t. 3a_{16} + 6a_{26}+ 7a_{36} \le16 \\

a_{ij} \in Z

\]

求解结果得$ \alpha_6 = [5,0,0]^T, \sigma_6 = 0\(,reduced cost 不为负数，因此不用将\) \alpha_6$加入RMP，列生成算法结束。

最终，我们求解最后一次迭代的RMP：

\[min (y_1 +...+y_3+y_4+y_5) \\

R1: 5y_1+0y_2+0y_3 +1y_4+1y_5\ge 25 \\

R2: 0y_1+2y_2+0y_3+2y_4+1y_5 \ge 20 \\

R3: 0y_1+0y_2+2y_3+0y_3 +1y_5\ge 18 \\

\]

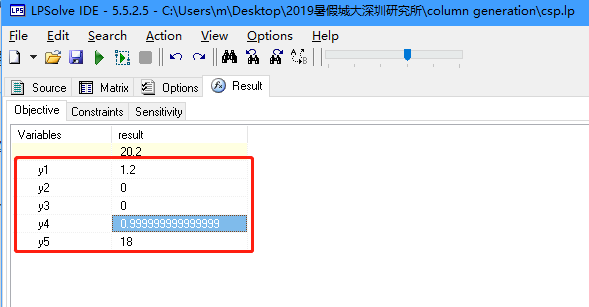
得到RM的最优解\(y = [1.2, 0,0,1, 18]\),聪明的同学已经主要到了，\(y_1=1.2\)怎么出现了小数呢，按理说y应该是整数才对啊。回到原问题RM：

\[min (y_1 +...+y_n) \\

R1: a_{11}y_1+...+a_{1n}y_n \ge 25 \\

R2: a_{21}y_1+...+a_{2n}y_n \ge 20 \\

R3: a_{31}y_1+...+a_{3n}y_n \ge 18 \\

\]

我们并没有加上\(y_i \in Z\)这个约束，这是因为我们在用列生成的时候把这个模型给松弛为了线性模型，毕竟列生成是用于求解linear program的。如果要求解大规模整数规划问题，列生成是无法办到的，后面我们会介绍结合column generation的branch and price方法。

至此，我们已经完完整整把列生成算法给走了一遍。相信列生成算法的原理已经深入各位读者的心里啦。

06 列生成代码

关于Cutting Stock Problem的列生成java代码，可以关注我们的公众号：

请关注公众号【程序猿声】，后台回复【cgcsp】，不包括【】即可下载！

07 reference