【MOCO基础】Pointer Networks原理及代码实现分析(Oriol Vinyals, 2015)
Pointer Networks
Paper: Vinyals O, Fortunato M, Jaitly N. Pointer networks[J]. Advances in neural information processing systems, 2015, 28.
链接:Pointer Networks
文章目录
- Pointer Networks
- 1. Ptr-Nets可以解决什么问题?
- 2. Ptr-Nets模型构建过程
-
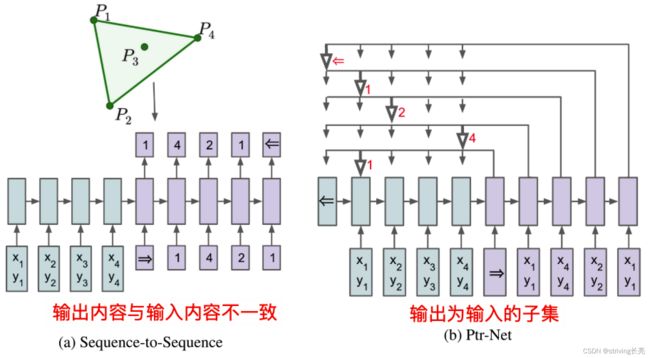
- 2.1 Ptr-Nets VS Seq2seq
- 2.2 Bahdanau Attention
- 2.3 Ptr-Nets原理
- 2.4. Ptr-Nets的实际表现
- 3. Ptr-Nets代码实现
-
- 3.1 数据预处理
- 3.2 PointerLSTM
- 3.3 模型训练及测试
- 总结
- 参考
1. Ptr-Nets可以解决什么问题?
Seq2seq是目前一个非常火的模型,在各领域都取得了广泛的应用,但是在传统的seq2seq中,依旧存在着一系列关键问题,比如:
-
在我之前的文章也提到过的“信息过长,信息丢失”的问题(文章链接:【自然语言处理】1. 细讲:Attention模型的机制原理),该问题可利用Soft Attention、Self-Attention有效解决 。
-
此外,Seq2seq中的输入点和输出点的数量是不固定的。
传统的seq2seq模型无法解决输出序列的词汇表会随着输入序列长度的改变而改变的问题,因为有些问题在输出的每一步中目标输出的数量取决于输入的长度,而输入的长度是可变的。 诸如对可变大小的序列进行排序等问题,以及各种组合优化问题都属于这类问题。对于这类问题,输出往往是输入集合的子集或者输出等于输入。
基于所面临的第二种问题,这篇文章引入了一种新的神经结构来学习输出序列的条件概率,其输出元素是与输入序列中的位置相对应的离散令牌(discrete tokens)。指针网络模型(Pointer Networks,Ptr-Nets)是在seq2seq模型的基础上引入一种结构类似编程语言中的指针,每个指针对应输入序列的一个元素,从而我们可以直接操作输入序列而不需要特意设定输出词汇表。
2. Ptr-Nets模型构建过程
2.1 Ptr-Nets VS Seq2seq
与以前的注意尝试的不同之处在于,Ptr-Nets不是在每个解码器步骤中使用注意将编码器的隐藏单元混合到上下文向量,而是使用注意力作为指针来选择输入序列的一个成员作为输出。
Ptr-Nets可以用来学习三个具有挑战性的几何问题(平面凸包问题、Delaunay三角剖分和旅行商问题TSP)的近似解。 生成的模型以纯数据驱动的方式(即,当我们只有输入和期望输出的示例时)为这些问题提供近似解决方案。Ptr-Nets不仅在输入注意力的情况下提高了seq2seq的一致性,而且还允许推广到可变大小的输出词典,输出字典的大小取决于输入序列的长度的组合。 实验结果表明,学习的模型泛化超过了它们被训练的最大长度。
由于可能的输出序列的组合数,寻找最优序列C在计算上是不切实际的。 取而代之的是,在Ptr-Nets中还引入波束搜索(beam search)过程来找到给定波束大小的最佳可能序列。
在Seq2seq中,因为输出是从输入中选择的,输出字典大小是固定的并且等于输入N。 因此,当输入n产生变化时,模型也要重新训练,模型无法学习具有大小依赖于输入序列长度的输出字典的问题的解决方案。
在输出数为O(n)的假设下,该模型的计算复杂度为O(n)。 针对于我们正在处理的问题,其精确算法成本更高。 例如,凸包问题的复杂度为 O ( n l o g n ) O(n log n) O(nlogn)。 注意力机制为这个模型增加了更多的“计算能力”。
2.2 Bahdanau Attention
Attention机制将固定的中间表示 C 换成根据当前 Encoder 的输出调整变化的 C i C_{i} Ci, 由 Bahdanau 等人提出并应用于机器翻译任务中,作为Soft Attention的一种,也是Attention机制的开山之作,Bahdanau Attention得到了广泛的应用。
在之前的文章,我已经对Attention的实现过程做了详细的介绍(链接:【自然语言处理】2. Attention实现详细解析( tfa, keras 方法调用源码分析 & 自建网络)),现在再重温一下,如图所示:

e i t e_{i t} eit是 t 时刻每一个编码状态 h i h_{i} hi与 Z t − 1 Z_{t-1} Zt−1结合所生成的值,表示该时刻之前的解码状态 Z t − 1 Z_{t-1} Zt−1受到编码状态 h i h_{i} hi 的影响程度。t 时刻 Z t − 1 Z_{t-1} Zt−1对输入序列各位置的“注意力”大小, 即对所有编码状态的权重分布, 可通过 Softmax 函数得到,其执行过程如下:
e i t = V a ∗ tanh ( W a Z t − 1 + U a h i ) s i t = exp ( e i t ) ∑ j = 1 n exp ( e j t ) ∑ i = 1 n s i t = 1 e_{i t}=V_{a} * \tanh \left(W_{a} Z_{t-1}+U_{a} h_{i}\right) \\ s_{i t}=\frac{\exp \left(e_{i t}\right)}{\sum_{j=1}^{n} \exp \left(e_{j t}\right)} \\ \sum_{i=1}^{n} s_{i t}=1 eit=Va∗tanh(WaZt−1+Uahi)sit=∑j=1nexp(ejt)exp(eit)i=1∑nsit=1
其中, V a V_{a} Va、 W a W_{a} Wa以及 U a U_{a} Ua均为网络的可训练参数。 C t C_{t} Ct 为对所有编码状态的动态加权和, C t C_{t} Ct 与 y t − 1 、 y_{t-1} 、 yt−1、Z_{t-1}$结合并得到 Z t Z_{t} Zt ,公式如下:
C t = ∑ i = 1 n s i t h i Z t = R N N ( y t − 1 , C t , Z t − 1 ) C_{t}=\sum_{i=1}^{n}s_{it}h_{i} \\ Z_{t}=RNN(y_{t-1},C_{t},Z_{t-1}) Ct=i=1∑nsithiZt=RNN(yt−1,Ct,Zt−1)
注意:我和论文中的字母表示不太一样,但所代表的意思以及执行过程是一样的。
在得到每一个时间步的解码状态之后,模型可通过全连接层以及输出函数给出对应位置的预测输出。通过注意力机制,在生成每个输出时,模型都可动态地关注到不同位置的编码状态,从而使得模型具有更好的拟合能力以及更强的可解释性。
在Ptr-Nets中,Encoder以及Decoder层的隐藏层节点数均为512。注意,对于每一个输出,我们必须执行N个操作,因此在推断时的计算复杂度变成 O ( n 2 ) O(n^2) O(n2)。
传统的Soft Attention模型不适用于输出字典大小依赖于输入向量的组合优化问题。
2.3 Ptr-Nets原理
如图所示,注意这个阶段只发生在预测阶段(Free-Run运行模式),因为Train阶段我们是教师强制(Teach-Force)运行模式,因此是不需要选的,因此我们选出来的输入序列的第1个item,将作为DecoderCell1的输入并产生新的输出。将新的输出与enc_output做Attention,重复Pointer选取的步骤,能够得到另一个预测结果。
这里就显示出Pointer机制了,因为我们是通过“引用”输入序列,作为我们的预测结果,而不是预测了一个新的东西。就像C语言里的指针(Pointer)一样,指针没有单独开辟内存空间(除了自身所占的几个byte),但却能指向具有内容的内存地址,使我们通过指针能直接访问相应的内容。
该模型实际就是对注意力模型做了一个非常简单的修改,从而允许我们应用端到端的方法来解决组合优化问题,其中输出字典的大小取决于输入序列中元素的数量,Ptr-Nets直接将softmax之后得到的概率当成了输出,让其承担指向输入序列特定元素的指针角色。
其实很简单,与Bahdanau Attention相比,Ptr-Nets仅仅采用两步,去除了求解 C i C_{i} Ci的过程,仅仅使用 e i j e_{ij} eij作为指向输入元素的指针,并通过Softmax函数选出最大概率输入元素并作为当前步的输出,在Ptr-Nets中,计算公式如下:
e i t = V a ∗ tanh ( W a Z t − 1 + U a h i ) s i t = exp ( e i t ) ∑ j = 1 n exp ( e j t ) e_{i t}=V_{a} * \tanh \left(W_{a} Z_{t-1}+U_{a} h_{i}\right) \\ s_{i t}=\frac{\exp \left(e_{i t}\right)}{\sum_{j=1}^{n} \exp \left(e_{j t}\right)} eit=Va∗tanh(WaZt−1+Uahi)sit=∑j=1nexp(ejt)exp(eit)
在t时刻,模型会根据上一个解码器Decoder的输出 Z t − 1 Z_{t-1} Zt−1和每一个输入元素计算所得出的概率值选择概率最大的 s i t s_{it} sit所对应的输入元素作为其Decoder的当前时刻输出 y t y_{t} yt,然后继续计算 Z t + 1 Z_{t+1} Zt+1,并直到所有的输入元素均被Decoder输出为止。
Z t + 1 = R N N ( y t , Z t ) Z_{t+1}=RNN(y_{t},Z_{t}) Zt+1=RNN(yt,Zt)
该方法专门针对输出是离散的并与输入中的位置相对应的问题,比如直接使用RNN输出目标点的坐标。
2.4. Ptr-Nets的实际表现
由于我的研究主要是TSP、VRP以及基于此的衍生优化问题,因此我会重点介绍该模型在TSP问题上的实际表现,凸包问题、Delaunay三角剖分问题的实验结果详见论文。
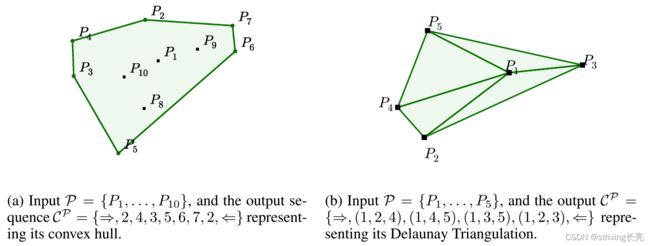
以上是Ptr-Nets在凸包问题、Delaunay三角剖分问题上的表现实例。
TSP:给定一个城市列表,我们希望找到一个最短的路线,每个城市访问一次,并返回到起点。 另外,我们假设两个城市之间的距离在每一个相反的方向是相同的。 这是一个NP-hard问题。
数据生成: 输入/输出是( P P P, C p C^p Cp)的格式。 P P P将是代表城市的笛卡尔坐标,这些城市是在[0,1]×[0,1]平方中随机选择的。 C p C^p Cp={ c 1 , . . . , c n c_{1},...,c_{n} c1,...,cn}将是表示最优路径(或游览)的1到n的整数的排列。 为了一致性,在训练数据集中,数据集总是从第一个城市开始,而不损失一般性。 为了生成精确的数据,城市数量不一样,所构建的数据集输出结果方式也不一样,具体地说:
- 在城市数量n<=20的情况下,本文采用Held-Karp算法(复杂度 O ( 2 n n 2 ) O(2^nn^2) O(2nn2))。
- 对于较大的n(大于20),产生精确解是极其昂贵的,本论文考虑了产生近似解的算法:A1和A2(均为启发式搜索算法,复杂度 O ( n 2 ) O(n^2) O(n2)),以及A3(复杂度 O ( n 3 ) O(n^3) O(n3))。 后一种算法保证在离最优长度1.5倍的范围内找到一个解。
作者并没有对Ptr-nets进行广泛的体系结构或超参数搜索,作者在所有的实验和数据集中都使用了几乎相同的体系结构。 具体地:
- 所有模型都使用了具有256或512个隐藏单元的单层LSTM
- 使用随机梯度下降(SGD)训练
- 学习率为1.0
- batch size为128
- 随机均匀权重初始化从-0.08到0.08
- L2正则化梯度裁剪为2.0

如上图所示,这是模型在凸包(左),Delaunay三角剖分(中)和TSP(右)上的表现,在m个点上训练,并在n个点上测试。 凸包的LSTM Seq2seq模型的一个失败在(a)中显示。 请注意,baseline不能应用于与训练不同的长度(没有加Attention机制,而是直接最后一个Encoder单元的输出,不适用于变长输入序列)。 对于n=5的PTR-Net模型,该模型获得了80.7%的正确率和93.0%的三角形覆盖率。 当n=10时,准确率为22.6%,三角形覆盖率为81.3%。 对于n=50,该模型没有产生任何精确正确的三角剖分,但得到了52.8%的三角覆盖。 有关n=50的示例,请参见中间一列。

上表显示了我们在TSP上的所有结果。与凸包和Delaunay三角剖分不同,解码器是不受约束的,在这个例子中,我们将波束搜索(beam Search)过程设置为只考虑有效旅程。 否则,Ptr-Nets模型有时会输出无效的旅游–例如,它会重复两个城市或决定忽略一个目的地(已被选的城市将会被Masked,从而以防下一次再被选择)。 此过程适用于n>20,其中至少有10%的实例不会产生任何有效的游览。
表中的第一组行显示了在最优数据上训练的Ptr-Nets,除了n=50,因为这在计算上是不可行的(本文为每个n训练了一个单独的模型)。 有趣的是,当使用最差的算法(A1)数据来训练Ptr-Net时,我们的模型优于试图模仿的A1算法(6.42 < 6.46)。
表中的第二组行显示了在5到20个城市的最佳数据上训练的Ptr-Nets如何能够推广到更多的城市。 结果对于n=25来说几乎是完美的,对于n=30来说是好的,但在40或更长的时间里似乎会崩溃(尽管如此,结果还是比偶然要好得多)。
3. Ptr-Nets代码实现
论文提供了数据集,以供我们展开实验验证,数据集链接:http://goo.gl/NDcOIG
Pointer-networks代码参考链接:https://github.com/keon/pointer-networks.git,基于此,我又做了一定的修改。
python版本信息:
python==3.7.13
keras==2.4.3
tensorflow==2.4.0
numpy==1.19.5
3.1 数据预处理
由于论文中给了数据集,与所提供的代码链接不同,我并没有采用“自己生成数据集,再采用动态规划等算法生成最优路径”的方式,而是直接采用论文数据集,以TSP5为例,论文所提供数据格式如下:

默认的训练数据集为1百万条,测试数据集为1万条,我仅仅采用了1000条训练数据以及100条测试数据。
from keras.models import Model
from keras.layers import LSTM, Input
from keras.utils.np_utils import to_categorical
from PointerLSTM import PointerLSTM
import numpy as np
import matplotlib.pyplot as plt
####TSP5数据集(From paper, url:http://goo.gl/NDcOIG)
print(".......preparing dataset.......")
list_test = []
list_train = []
list_train_x = [] # 训练数据集-输入x
list_train_y = [] # 训练数据集-输出y
list_test_x = [] # 测试数据集x
list_test_y = [] # 测试数据集y
absolute_path=r"/Users/changliang/codes/pythonPycharm/pointer-networks/tsp5_data_paper" # 我的文件路径
with open(absolute_path+'/tsp5_test.txt') as file_test,open(absolute_path+'/tsp5.txt') as file_train:
for line in file_test.readlines():
f = line.strip().split() # strip()默认删除空白符(包括'\n', '\r', '\t', ' ') split()默认为空格
list_test.append(f)
for line in file_train.readlines():
f = line.strip().split()
list_train.append(f)
train_size=1000
test_size=100
# (10000, 5, 5)----->(10000, 5)
list_test_x = np.array(list_test)[:,:10].reshape(len(list_test),5,2).astype("float32")[:test_size,:]
list_test_y = np.array(list_test)[:,11:-1].astype("int8")-1 # 因为原始的output是从1开始的
list_test_y = to_categorical(list_test_y)[:test_size,:] # 变成one-hot形式
# (1000000, 5, 5)----->(1000000, 5)
list_train_x = np.array(list_train)[:,:10].reshape(len(list_train),5,2).astype("float32")[:train_size,:]
list_train_y = np.array(list_train)[:,11:-1].astype("int8")-1
list_train_y = to_categorical(list_train_y)[:train_size,:]
说生成的训练输入数据shape为(1000,5,2),输出数据为(100,5,5)
3.2 PointerLSTM
关于如何自定义Keras可以参看这里:链接1、链接2、链接3
Keras实现自定义网络层。需要实现以下几个方法:(注意input_shape是包含batch_size项的)
- init():保存成员变量的设置
- build(input_shape): 这是你定义权重的地方。这个方法必须设 self.built = True,可以通过调用 super([Layer], self).build() 完成。值得注意的是:在call()函数第一次执行时会被调用一次,这时候可以知道输入数据的shape,init()函数中只初始化了输出数据的shape,而输入数据的shape需要在build()函数中动态获取,这也解释了为什么在有__init__()函数时还需要使用build()函数。
- call(x): 这里是编写层的功能逻辑的地方。你只需要关注传入 call 的第一个参数:输入张量,除非你希望你的层支持masking。即当其被调用时会被执行。
- compute_output_shape(input_shape): 如果你的层更改了输入张量的形状,你应该在这里定义形状变化的逻辑,这让Keras能够自动推断各层的形状。
# PointerLSTM
import keras.backend as K
from keras.activations import tanh, softmax
from keras.engine import InputSpec
import keras
import numpy as np
import tensorflow as tf
class Attention(keras.layers.Layer):
"""
Attention layer
"""
def __init__(self, hidden_dimensions, name='attention'):
super(Attention, self).__init__(name=name, trainable=True)
self.W1 = keras.layers.Dense(hidden_dimensions, use_bias=False)
self.W2 = keras.layers.Dense(hidden_dimensions, use_bias=False)
self.V = keras.layers.Dense(1, use_bias=False)
def call(self, encoder_outputs, dec_output, mask=None):
w1_e = self.W1(encoder_outputs)
w2_d = self.W2(dec_output)
tanh_output = tanh(w1_e + w2_d)
v_dot_tanh = self.V(tanh_output)
if mask is not None:
v_dot_tanh += (mask * -1e9)
attention_weights = softmax(v_dot_tanh, axis=1)
att_shape = K.shape(attention_weights)
return K.reshape(attention_weights, (att_shape[0], att_shape[1]))
class Decoder(keras.layers.Layer):
"""
Decoder class for PointerLayer
"""
def __init__(self, hidden_dimensions):
super(Decoder, self).__init__()
self.lstm = keras.layers.LSTM(
hidden_dimensions, return_sequences=False, return_state=True) # only need the last decoder cell
def call(self, x, hidden_states):
dec_output, state_h, state_c = self.lstm(
x, initial_state=hidden_states)
return dec_output, [state_h, state_c]
def get_initial_state(self, inputs):
return self.lstm.get_initial_state(inputs)
def process_inputs(self, x_input, initial_states, constants):
return self.lstm._process_inputs(x_input, initial_states, constants)
class PointerLSTM(keras.layers.Layer):
"""
PointerLSTM
"""
def __init__(self, hidden_dimensions, name='pointer', **kwargs):
super(PointerLSTM, self).__init__(
hidden_dimensions, name=name, **kwargs)
self.hidden_dimensions = hidden_dimensions
self.attention = Attention(hidden_dimensions)
self.decoder = Decoder(hidden_dimensions)
def build(self, input_shape):
super(PointerLSTM, self).build(input_shape)
self.input_spec = [InputSpec(shape=input_shape)]
def step(self, x_input, states):
x_input1 = K.expand_dims(x_input,1)
input_shape = self.input_spec[0].shape
en_seq = states[-1] # shape(input_size,hidden_size)
_, [h, c] = self.decoder(x_input1, states[:-1])
dec_seq = K.repeat(h, input_shape[1]) # repeat for compute with each encoder cell ,shape(input_size,hidden_size)
probs = self.attention(en_seq,dec_seq,selected_cities = self.selected_cities)
return probs, [h, c]
def call(self, x, training=None, mask=None, states=None):
"""
:param Tensor x: Should be the output of the encoder
:param Tensor states: last state of the encoder
:param Tensor mask: The mask to apply
:return: Pointers probabilities
"""
input_shape = self.input_spec[0].shape
en_seq = x
x_input = x[:, input_shape[1] - 1, :]
x_input = K.repeat(x_input, input_shape[1])
if states:
initial_states = states
else:
initial_states = self.decoder.get_initial_state(x_input)
constants = []
preprocessed_input, _, constants = self.decoder.process_inputs(
x_input, initial_states, constants)
constants.append(en_seq)
last_output, outputs, states = K.rnn(self.step, preprocessed_input,
initial_states,
go_backwards=self.decoder.lstm.go_backwards,
constants=constants,
input_length=input_shape[1],
zero_output_for_mask=True)
return outputs
def get_output_shape_for(self, input_shape):
# output shape is not affected by the attention component
return (input_shape[0], input_shape[1], input_shape[1])
def compute_output_shape(self, input_shape):
return (input_shape[0], input_shape[1], input_shape[1])
其中,Attention类是所设计的概率生成方式(本代码并没有将已有的城市Mask)
class Attention(keras.layers.Layer):
"""
Attention layer
"""
def __init__(self, hidden_dimensions, name='attention'):
super(Attention, self).__init__(name=name, trainable=True)
self.W1 = keras.layers.Dense(hidden_dimensions, use_bias=False)
self.W2 = keras.layers.Dense(hidden_dimensions, use_bias=False)
self.V = keras.layers.Dense(1, use_bias=False)
def call(self, encoder_outputs, dec_output, mask=None):
w1_e = self.W1(encoder_outputs)
w2_d = self.W2(dec_output)
tanh_output = tanh(w1_e + w2_d)
v_dot_tanh = self.V(tanh_output)
if mask is not None:
v_dot_tanh += (mask * -1e9)
attention_weights = softmax(v_dot_tanh, axis=1)
att_shape = K.shape(attention_weights)
return K.reshape(attention_weights, (att_shape[0], att_shape[1]))
3.3 模型训练及测试
print(".......preparing dataset complete.......")
hidden_size = 256
seq_len = 5
nb_epochs = 200
learning_rate = 0.01
batch_size=128
print(".......building model.......")
main_input = Input(shape=(seq_len, 2), name='main_input') # input shape(seq_len, feature_num) 此处为二维坐标 (5,2)
encoder,state_h, state_c = LSTM(hidden_size,return_sequences = True, name="encoder",return_state=True)(main_input)
decoder = PointerLSTM(hidden_dimensions=hidden_size, name="decoder")(encoder,states=[state_h, state_c])
model = Model(main_input, decoder)
print(model.summary())
# "sparse_categorical_accuracy" :y_以数值形式给出,y以独热码给出,如y_ = [1], y = [0.256,0.695,0.048]
# "categorical_accuracy" :y_是以独热形式给出,y以独热码给出,如y_ = [0,1,0], y = [0.256,0.695,0.048]
model.compile(optimizer='adam',
loss='categorical_crossentropy',
metrics=['categorical_accuracy'])
history = model.fit(list_train_x, list_train_y, epochs=nb_epochs, batch_size=batch_size,
validation_data=(list_test_x,list_test_y), validation_freq=1)
loss = history.history['loss']
val_loss = history.history['val_loss']
plt.plot(loss, label='Training Loss')
plt.plot(val_loss, label='Validation Loss')
plt.title('Training and Validation Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.legend()
plt.show()#展示
acc = history.history['categorical_accuracy']
val_acc = history.history['val_categorical_accuracy']
plt.plot(acc, label='Training Accuracy')
plt.plot(val_acc, label='Validation Accuracy')
plt.title('Training and Validation Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.legend()
plt.show()#展示
print("------------Results Presentation --------------")
#print(model.predict(x_test))
print('model evaluate : \n ',model.evaluate(list_test_x,list_test_y))
print("model prediction result \n",np.argmax(model.predict(list_test_x), axis=1))
#print(to_categorical(y_test))
print("True result \n",np.argmax(list_test_y, axis=1))
# save model
model.save_weights('model_weight_tsp5.hdf5')
代码总体还是比较简单的,没什么可讲解的。
由于仅仅是一个示例,我并没有做很多的优化,该模型依旧有很多可优化的地方,实验结果我就不放出来了,有兴趣的,或者有哪些地方不明白的可以留言,或者直接与我进行交流哈~
总结
Pointer Networks天生具备输出元素来自输入元素这样的特点,于是它非常适合用来实现“复制”这个功能。在自然语言处理领域,很多研究者也确实把它用于复制源文本中的一些词汇。另外由于摘要这个任务所需的词汇较多,也非常适合使用复制的方法来复制一些词。这就造成了目前Pointer Networks成为文本摘要方法中的利器的局面。
此外,在组合优化领域,Ptr-Nets也得到了广泛的应用,并已成为组合优化问题的端到端方法的入门模型,后来基于此模型,研究者也进行了很多改进,比如与强化学习结合,将Attention换成Transformer中采用的Self- Attention等。总之,Ptr-Nets为组合优化的端到端解决办法起了一个好头,并促使广大研究者进行更加深入的研究。
参考
- https://zhuanlan.zhihu.com/p/260745795


