深度网络架构的设计技巧(二)之BoT：Bottleneck Transformers for Visual Recognition

单位：UC伯克利，谷歌研究院(Ashish Vaswani, 大名鼎鼎的Transformer一作）
ArXiv：https://arxiv.org/abs/2101.11605
Github：https://github.com/leaderj1001/BottleneckTransformers

导读：
Transformer一词来自本文作者之一的Ashish Vaswani，了解Transformer的人或许知道Original Transformer，另一个说法叫Vaswani Transformer。而ViT刚出来就引爆学术圈，各大CNN任务用Transformer翻一遍就能达到SOTA；而现在是Transformer+自监督学习，即MAE的天下。本文向经典致敬，向大佬学习如何设计有效的深度网络，即在ResNet BottleNeck内如何引入多头注意力。

---

---

一、摘要

作者提出一个网络叫BoTNet，一个概念简单但强大的骨架模型，使用自注意力解决多个计算机视觉任务，如分类，检测与分割等。通过仅仅将ResNet骨架后三个基本模块中的空间CNN，替换为全局注意力而没有其他改变，该方法就能提升基线方法的性能，同时能够减少参数量和最小的延迟开销。通过BoTNet的设计，作者指出带有自注意力的ResNet模块也能当作Transformer模块。Without bells and whistles，避免花里胡哨，BoTNet超过了当前单模型单尺度的ResNeSt；在ImageNet-1K上获得84.7%的Top1精度，并且在TPU-v3上比EfficientNet快1.6倍。一个简单的模块替换，就能涨点与加速，又快又好！

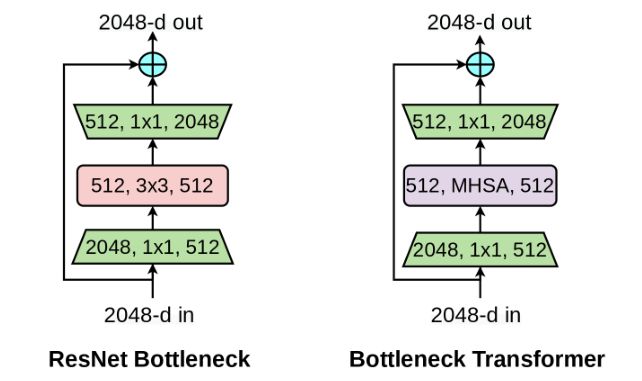
作者的核心设计即BottleNeck Transformer，将MHSA多头注意力替换原来$3\times 3$的卷积操作，一眼看穿！

二、引言

深度卷积骨架模型在图像分类、目标检测与实例分割中取得了重大进展。很多具有标志性的骨架架构采用$3\times 3$的多卷积层，如VGG，ResNet等。尽管CNN能够有效地捕捉局部信息，视觉任务如目标检测，实例分割和关键点检测需要建模长距离的依赖。例如，在实例分割中，能够从大范围里收集和关联场景信息将有利于学习目标之间的联系。为了全局聚合局部滤波器的响应，基于CNN的架构通常需要堆叠多层网络。尽管，这样做确实可以提升性能，但一种能够显式地建模全局（非局部）的机制能够更强大和可扩展，而不需要那么多层。

In order to globally aggregate the locally captured filter responses, convolution based architectures require stacking multiple layers [54, 28]. Although stacking more layers indeed improves the performance of these backbones [67], an explicit mechanism to model global (non-local) dependencies could be a more powerful and scalable solution without requiring as many layers.

对于NLP（natural language processing自然语言处理）来说，建模长距离依赖同样至关重要。自注意力是一种可计算的原作，它通过基于内容的寻址机制实现配对实体之间的交互，从而在长序列之间学习丰富的关联特征的层次架构。这成为了NLP中Transformer块的标准工具，突出的例子有GPT，BERT等。

一个简单使用视觉自注意力的方法就是Transformer中的多头注意力MHSA层来替换空间CNN层。最近这种方法已经从两个方面开展：1、一些模型如SASA，AACN，SANet，Axial-SASA等使用不同形式的自注意力如local, global, vertor, axial等去替换ResNet中的BottleNeck，另一方面就是ViT，它使用堆叠的Transformer块，在不重叠的图像块的线性映射上操作。这两类方法看似提出了不同的架构，但是作者觉得，ResNet BottleNeck with MHSA是某种类型的Transformer Block，除了残差连接和归一化层的微小差别。因此，作者将这种称为BottleNeck Transformer，即BoT。

三、结构

左：规范的Transformer结构；中：BottleNeck Transformer；右：一种BoT的实现，基于ResNet BottleNeck。

带有相对位置编码的多头注意力模块。自注意力层在带有可分离的相对位置编码的2D特征图上操作的，注意力逻辑表示是$q{k}^T+q{r}^T$，其中$q,k,r$代表询问、键和相对位置编码。

3.1 相对位置编码

在视觉任务中，相对位置编码更加合适，在多个模型中展现出优势。这样，自注意力不仅考虑数据内容的信息，也考虑了数据之间的相对位置。

通过以上表格，带有绝对位置编码的AP为42.5，小于相对位置编码的AP即43.6。相对位置编码，具有优势。

3.2 代码解读

class BottleBlock(nn.Module):
    def __init__(
        self,
        *,
        dim,
        fmap_size,
        dim_out,
        proj_factor,
        downsample,
        heads = 4,
        dim_head = 128,
        rel_pos_emb = False,
        activation = nn.ReLU()
    ):
        super().__init__()

        # shortcut

        if dim != dim_out or downsample:
            kernel_size, stride, padding = (3, 2, 1) if downsample else (1, 1, 0)

            self.shortcut = nn.Sequential(
                nn.Conv2d(dim, dim_out, kernel_size, stride = stride, padding = padding, bias = False),
                nn.BatchNorm2d(dim_out),
                activation
            )
        else:
            self.shortcut = nn.Identity()

        # contraction and expansion

        attn_dim_in = dim_out // proj_factor
        attn_dim_out = heads * dim_head

        self.net = nn.Sequential(
            nn.Conv2d(dim, attn_dim_in, 1, bias = False),
            nn.BatchNorm2d(attn_dim_in),
            activation,
            Attention(
                dim = attn_dim_in,
                fmap_size = fmap_size,
                heads = heads,
                dim_head = dim_head,
                rel_pos_emb = rel_pos_emb
            ),
            nn.AvgPool2d((2, 2)) if downsample else nn.Identity(),
            nn.BatchNorm2d(attn_dim_out),
            activation,
            nn.Conv2d(attn_dim_out, dim_out, 1, bias = False),
            nn.BatchNorm2d(dim_out)
        )

        # init last batch norm gamma to zero

        nn.init.zeros_(self.net[-1].weight)

        # final activation

        self.activation = activation

    def forward(self, x):
        shortcut = self.shortcut(x)
        x = self.net(x)
        x = x + shortcut
        return self.activation(x)

注意力模块为：

class Attention(nn.Module):
    def __init__(
        self,
        *,
        dim,
        fmap_size,
        heads = 4,
        dim_head = 128,
        rel_pos_emb = False
    ):
        super().__init__()
        self.heads = heads
        self.scale = dim_head ** -0.5
        inner_dim = heads * dim_head

        self.to_qkv = nn.Conv2d(dim, inner_dim * 3, 1, bias = False)

        rel_pos_class = AbsPosEmb if not rel_pos_emb else RelPosEmb
        self.pos_emb = rel_pos_class(fmap_size, dim_head)

    def forward(self, fmap):
        heads, b, c, h, w = self.heads, *fmap.shape

        q, k, v = self.to_qkv(fmap).chunk(3, dim = 1)
        q, k, v = map(lambda t: rearrange(t, 'b (h d) x y -> b h (x y) d', h = heads), (q, k, v))

        q = q * self.scale

        sim = einsum('b h i d, b h j d -> b h i j', q, k)
        sim = sim + self.pos_emb(q)

        attn = sim.softmax(dim = -1)

        out = einsum('b h i j, b h j d -> b h i d', attn, v)
        out = rearrange(out, 'b h (x y) d -> b (h d) x y', x = h, y = w)
        return out

相对位置编码和绝对位置编码：

def rel_to_abs(x):
   b, h, l, _, device, dtype = *x.shape, x.device, x.dtype
   dd = {'device': device, 'dtype': dtype}
   col_pad = torch.zeros((b, h, l, 1), **dd)
   x = torch.cat((x, col_pad), dim = 3)
   flat_x = rearrange(x, 'b h l c -> b h (l c)')
   flat_pad = torch.zeros((b, h, l - 1), **dd)
   flat_x_padded = torch.cat((flat_x, flat_pad), dim = 2)
   final_x = flat_x_padded.reshape(b, h, l + 1, 2 * l - 1)
   final_x = final_x[:, :, :l, (l-1):]
   return final_x

def relative_logits_1d(q, rel_k):
   b, heads, h, w, dim = q.shape
   logits = einsum('b h x y d, r d -> b h x y r', q, rel_k)
   logits = rearrange(logits, 'b h x y r -> b (h x) y r')
   logits = rel_to_abs(logits)
   logits = logits.reshape(b, heads, h, w, w)
   logits = expand_dim(logits, dim = 3, k = h)
   return logits

# positional embeddings

class AbsPosEmb(nn.Module):
   def __init__(
       self,
       fmap_size,
       dim_head
   ):
       super().__init__()
       height, width = pair(fmap_size)
       scale = dim_head ** -0.5
       self.height = nn.Parameter(torch.randn(height, dim_head) * scale)
       self.width = nn.Parameter(torch.randn(width, dim_head) * scale)

   def forward(self, q):
       emb = rearrange(self.height, 'h d -> h () d') + rearrange(self.width, 'w d -> () w d')
       emb = rearrange(emb, ' h w d -> (h w) d')
       logits = einsum('b h i d, j d -> b h i j', q, emb)
       return logits

class RelPosEmb(nn.Module):
   def __init__(
       self,
       fmap_size,
       dim_head
   ):
       super().__init__()
       height, width = pair(fmap_size)
       scale = dim_head ** -0.5
       self.fmap_size = fmap_size
       self.rel_height = nn.Parameter(torch.randn(height * 2 - 1, dim_head) * scale)
       self.rel_width = nn.Parameter(torch.randn(width * 2 - 1, dim_head) * scale)

   def forward(self, q):
       h, w = self.fmap_size

       q = rearrange(q, 'b h (x y) d -> b h x y d', x = h, y = w)
       rel_logits_w = relative_logits_1d(q, self.rel_width)
       rel_logits_w = rearrange(rel_logits_w, 'b h x i y j-> b h (x y) (i j)')

       q = rearrange(q, 'b h x y d -> b h y x d')
       rel_logits_h = relative_logits_1d(q, self.rel_height)
       rel_logits_h = rearrange(rel_logits_h, 'b h x i y j -> b h (y x) (j i)')
       return rel_logits_w + rel_logits_h

四、实验

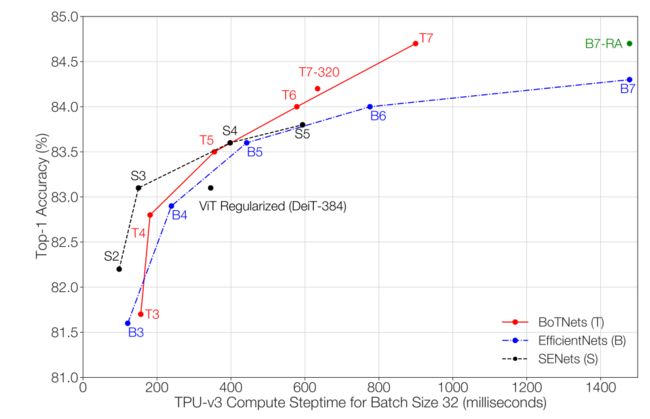
通过图表发现，BoTNet-T7展现出非常好的可扩展性，而BoTNet从T3到T5即堆叠的BoT块在3-5个内，优势并不明显。