电影兑换券的推荐策略——二分图最优匹配算法
动手点关注 干货不迷路
问题概述
一笔订单最多可使用所含电影票数目张兑换券。换而言之,用户选了几个座位,最多便能使用几张兑换券,兑换券有三个属性,分别是:
面值(元):在不支持补差的情况下,票价小于等于面值才可以使用
固定支付金额(元):满足兑换券的使用条件下,需要支付的钱。
补差(是 / 否):如果支持补差,当票价大于面值时,还需要额外支付 (票价 - 面值)元
举个栗子:小明有一张面值 50,固定支付 19 元且支持补差的兑换券。那么他能使用这张兑换券去购买票价小于等于 50 元的电影票,只需支付 19 元。因为支持补差,所以他能购买票价为 60 元(大于面值)的电影票,需支付(19 + ( 60 - 50))既 29 元。
我们问题是:用户下了一笔订单,订单中有 x(根据业务场景,x <= 6)张电影票,y 张兑换券,从这 y 张兑换券中选择不超过 x 张兑换券,使得该笔订单的实际支付金额最少,如果有多种解决方案,那么根据以下优先级为用户推荐选券的方案:
优先级 1: 选择实际支付金额少的方案
优先级 2: 如果实际支付金额一致,则优先使用面值小的方案
原因:如果用户想购买一张票价为 38 元的电影票,当前他有一张 40 元和一张 60 元的兑换券,任意使用一张兑换券能得到的实际支付金额都是 0 元,那么优先为用户选择 40 元的兑换券,这样 60 元的兑换券就能服务于用户的下一笔订单,更能为用户省钱。
优先级 3: 若面值大小也一致,则优先使用优惠券所在券包消耗券数目多的优惠券
优先级 4: 若消耗券数目一致,则优先使用过期时间早的优惠券
技术方案
方案一:贪心
具体步骤:排序
对票价从大到小排序,让票价高的电影票优先选择,目的就是为了金额大的电影票优先使用限制条件少(既面值大)的兑换券,让券面值得到充分利用,每个票和券的组合都尽可能是最优解。
证明方法:举反例法
很不幸,很快就找出一个反例推翻了这个方案,反例如图所示
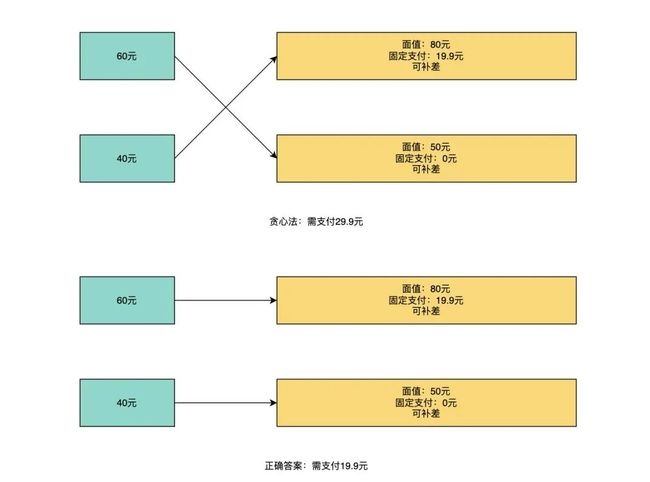
方案二:暴力枚举
枚举所有方案,从这所有方案中求出最优解,但是时间复杂度高达 C(y, x) * A(x, x) 也就是 O(n!),若按照 1s 钟计算机能运行 10^8 次计算这样的标准,当 n = 13 的时候,需要超过 10s 才能得到答案,并且 n 每增加 1,时间就会扩大 n 倍。
解决方案三:二分图最优匹配算法——KM 算法
km(Kuhn-Munkres)算法简介
km 算法是一种二分图最佳匹配算法,该算法主要用于解决一个经典的问题模型:完美婚姻问题。该问题的描述如下:n 个男生和 n 个女生相亲,第 i 个男生和第 j 个女生在一起的幸福值是 val(i, j),如何让 n 个男生和 n 个女生完成一一配对,使得这个整体的总幸福值最大。我们的问题和完美婚姻问题模型有点相似,并且经过调研 km 算法时间复杂度是 n^3,km 算法有一个非常大的优点就是,他可以求出哪张券用于哪张电影票,适用于选座相关的业务场景。
km 算法落地(对 km 算法不熟悉的同学可以先浏览第三部分)
我们把兑换券看成男生,电影票看成女生,用兑换券 j 购买电影票 i 的花费是 -w(i, j)去建图,如果兑换券 j 无法购买电影票 i,那么花费 w(i, j)设置为负无穷大,去构造一个二分图尝试求解,我们会遇到一些问题:
改造一:如何满足 km 算法的使用条件?
因为 km 算法是用于求解二分图的最佳匹配,也就是说二分图必须存在最佳匹配才能使用 km 算法求解。存在最佳匹配的必要条件是:必须两边的点相同,而且至少存在一种匹配方案使得所有的点都被匹配。所以我们需要补点和补边(补点和补边也是使用 km 算法的常见的技巧)。补边策略:将不存在的边,权重设为-inf。补点策略:新增 x 张兑换券,第 y + i 张兑换券跟第 i 张电影票连边,权值为电影票的原价,这样一来可以保障把无穷大的结果排除在外,二来不需要再额外再计算使用原价购买的情况。
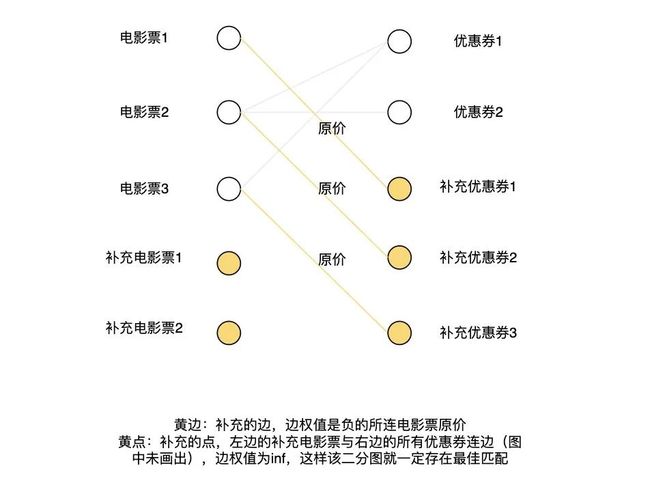
改造二:如何在多个解中求出满足优先级的解?
我们可以把所有兑换券按照面值由小到大排序,如果面值一致,那么按照入账时间从早到晚排序,如果入驻时间一致,按照过期时间由早到晚排序,简而言之,把优先级高的券放在前面。枚举数量 k,对前 k 个兑换券和所有的电影票加入 km 模型中,计算出最少花费,只有花费变得比之前更小才更新答案。这样可以保证取得最少花费的同时,还能满足优先级。还有一个好处是,如果后续 pm 对策略的优先级进行调整,那么我们可以更改最初的排序规则即可。但是时间复杂度此时变成了 n^4。
如图所示,当 k 等于 2 的时候取得最优解,k=3 的时候有可能匹配到优先级低的券。
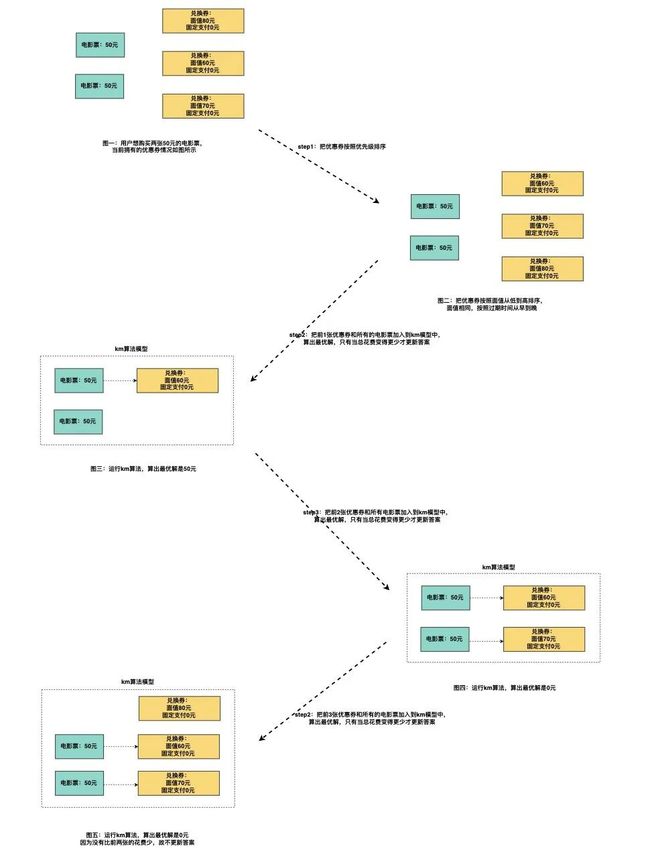
改造三、时间复杂度的优化
经过改造一和改造二的处理后,算法时间复杂度是:(x+y)^4 + y*logy(x 代表电影票张数,y 代表兑换券张数)
时间复杂度分析:经过补点操作后,二分图两边的点都是 x + y 个。因为 km 算法的时间复杂度是 n ^ 3 次方,n 为二分图单侧的点的个数。所以当前的时间复杂度是 (x+y)^3 。为了处理匹配的优先级问题,我们对优惠券进行了优先级排序,时间复杂度是y*logy,在运行 km 算法的时候,枚举了数量 k,所以总时间复杂度为(x+y)^4 + y*logy。
改造方法
具体步骤:对于每一张电影票,预处理出对于这张电影票优先级最高的 n(n 为当前的电影票张数)张,把这些兑换券去重,我们就能得到最多 nn 张兑换券。用着 nn 张兑换券代替原来的所有优惠券
时间复杂度(优化后,算法的时间复杂度跟优惠券数目无关,而跟电影票张数有关,目前的业务场景是,电影票最多不超过 4 张,所以该算法有较好的性能):
预处理出
x*x张优惠券的时间复杂度:x^2 * y * logx(x 为电影票数目,y 为优惠券数目)运行 km 算法求最优解的时间复杂度:
((1 + x) * x)^4 + 2 * x^2 *logx(x 为电影票数目)总时间复杂度:
x^2 * y * logx+((1 + x) * x)^4 + 2 * x^2 *logx(x 为电影票数目,且 0 < x <= 4)
收益:
当用户有 500 张兑换券(极限值时),能非常迅速的计算出最优策略,几乎无延迟。
km 原理证明
前置知识
二分图:又称作二部图,是图论中的一种特殊模型。设 G=(V,E)是一个无向图,如果顶点 V 可分割为两个互不相交的子集(A,B),并且图中的每条边(i,j)所关联的两个顶点 i 和 j 分别属于这两个不同的顶点集(i in A,j in B),则称图 G 为一个二分图。
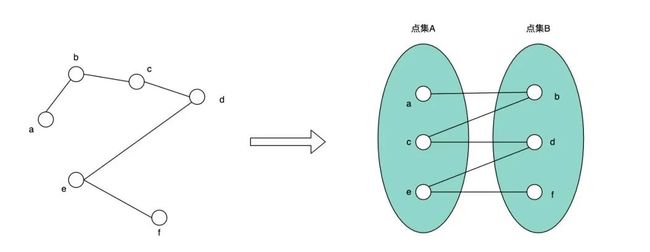
匹配:在二分图中,一个「匹配」(matching)是一组边的集合,其中任意两条边都没有公共顶点。
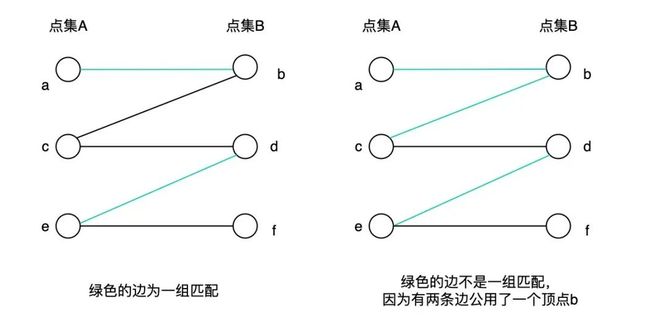
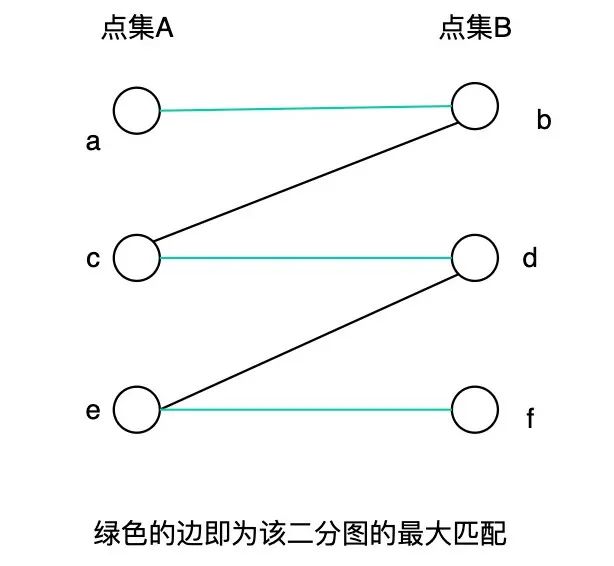
最大匹配:一个图所有匹配中,所含匹配边数最多的匹配,称为这个图的最大匹配。
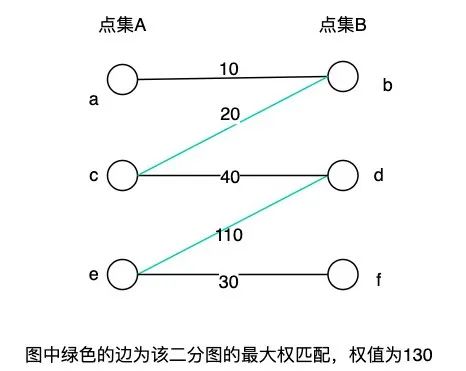
最大权匹配:在一个带边权的二分图的所有匹配中,边权和最大的匹配,称为这个图的最大权匹配。
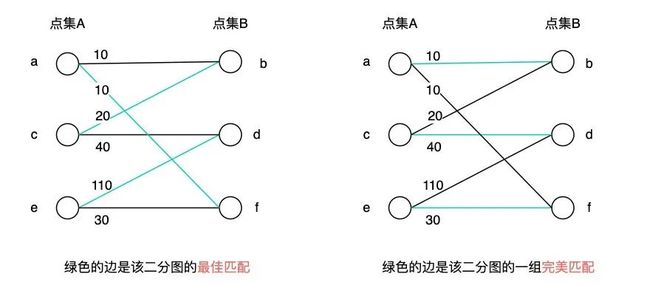
完美匹配:如果一个二分图的某个匹配中,所有的顶点都是匹配点,那么它就是一个完美匹配。
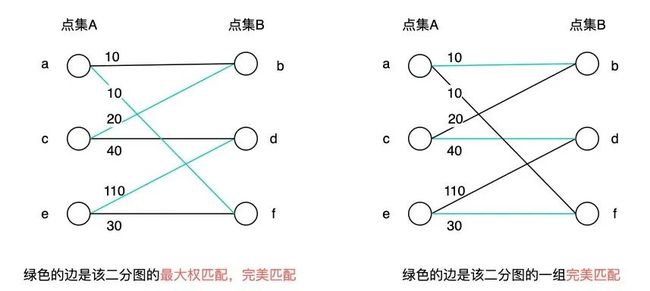
最佳匹配:二分图 G 的每条边都有权值,则权值和最大的完美匹配称为最佳匹配。
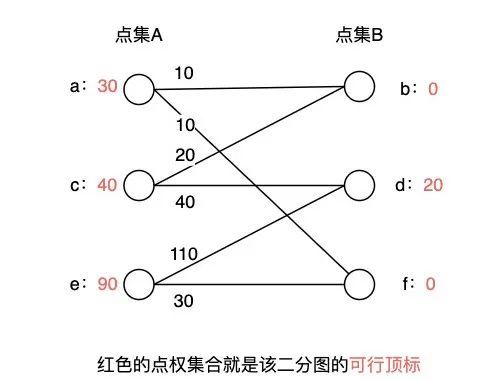
可行顶标:给二分图每个节点 i 分配一个权值 l(i) ,对于所有边(u, v) 满足 w(u, v) <= l(u) + l(v) 的点权集合。如图所示,集合 { a: 30, b: 0, c: 40, d: 20, e: 90, f: 0 } 就是该二分图的一组可行顶标。一个二分图有无数个可行顶标。
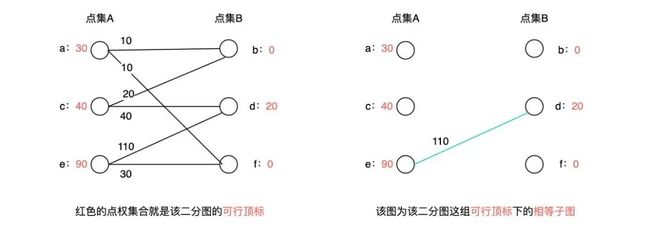
相等子图:对于某一组可行顶标,我们吧包含所有点但只包含满足 w(u, v) = l(u) + l(v) 的边的子图,称为该可行顶标下的生成子图。
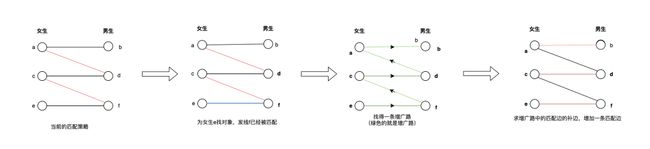
匈牙利算法(感兴趣可以自行百度学习):该算法用于求解二分图的最大匹配算法,核心策略如下:
如果能匹配,直接匹配
如果不能匹配,找一条增广路,对增广路(增广路定义:一条 非匹配边->匹配边->非匹配边->......->非匹配边 的路径。有的博客也叫交错路)的边取补边,来增加一条匹配边
km 依赖定理及证明
定理:
如果二分图存在某组可行顶标,并且该可行顶标的相等子图存在完美匹配,那么该匹配就是原二分图的最佳匹配。
证明:
考虑原二分图的任意一组完美匹配 M ,其边权和 val(M)等于每条匹配边(匹配边没有公共顶点)的权值和,又根据可行顶标的定义,我们可以得出任意一组完美匹配的边权和都小于等于任意一组可行顶标的点权和。
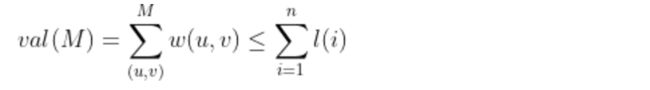
如果存在一组可行顶标且该可行顶标的相等子图存在完美匹配,那么该相等子图的完美匹配 M'的边权和 val(M')如下。(因为相等子图只存在 w(u, v) = l(u) + l(v) 的边)
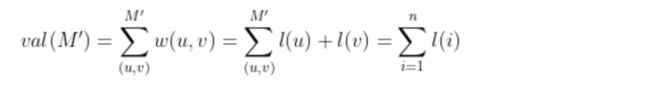
显然对于任意的完美匹配 M,val(M) <= val(M'),所以 M'就是权值和最大的完美匹配,即最佳匹配。
执行步骤
因为二分图两边点的个数相等,假设个数为 n。
首先我们要初始化二分图的可行顶标,二分图左边的点可行顶标取值为:以这个点为端点的最大边权值,二分图右边的点可行顶标取值为:0
我们依次为左边的点匹配,匹配准则是:可行顶标的和等于边权值。(满足相等子图)
对于左边节点 u 的匹配规则是:如果能匹配那么直接匹配,如果不能匹配就以 u 为起点,找交错路,这些交错路会组成一棵以节点 u 为根节点的交错树,树中的任意两条边都是满足匹配准则。如果存在一个叶子节点 v 与其父节点满足匹配准则,并且是非匹配边(存在增广路),那么进行增广操作(对增广路中的匹配边取补集),来增加一条匹配边。如果没有叶子节点满足匹配准则(叶子节点都是匹配点),那么就调整可行顶标的值,如何调整呢?
我们把二分图左边在交错树中的点集记为 S,右边在交错树中的点集记为 T,左边不在交错树中的点集记为 S',右边不在交错树的点集记为 T'
集合 S 中的点,可行顶标减少 slack_min
集合 T 中的点,可行顶标增加 slack_min
根据左右顶点所在集合,我们可以把二分图中的边分成 4 种:
左顶点在 S 中,右顶点在 T 中,可行顶部和不变,满足相等子图
左顶点在 S 中,右顶点在 T'中,可行顶标和变小,有可能加入相等子图,但是我们需要需要满足可行顶部的定义:可行顶部的和大于等于边权和,所以我们需要让slack_min 取值为 min(l(u) + l(v) - w(u, v)) , (u 为 S'中的点,v 为集合 T'中的点)
左顶点在 S'中,右顶点在 T 中,可行顶部和变大,不可能加入相等子图
左顶点在 S'中,右顶点在 T'中,保持不变
当一个新点 u 加入集合 T 有两种情况:
是未匹配点,则找到增广路
和 S'中的点已经匹配,继续增广,找 u'
这样每调整一轮可行顶标,集合 T 至少增加一个点,那么至多修改 n 次顶标后,就可以找到增广路。
代码运行过程演示
完美婚姻问题为例:现在有 3 男 3 女,不同的男生和不同的女生之间有不同的好感值,情况如图所示(如果没有连边,代表好感度为 0),我们希望让他们两两配对,使得整体的好感度最大。
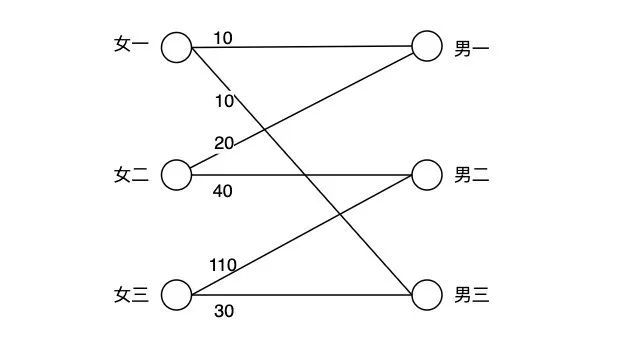
初始化策略:构造一个可行顶标,满足 w(u, v) <= l(u) + l(v),构造方案:所有男生可行顶标取值:0,所有女生取值:最大好感值
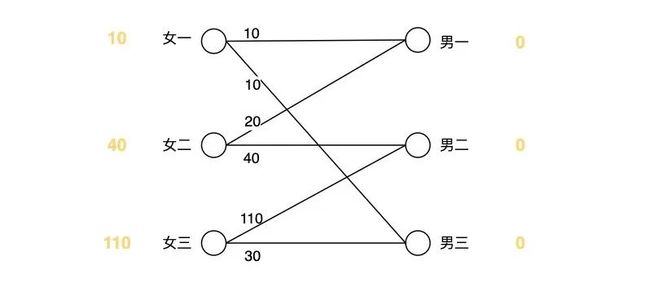
逐一为每个女生找对象,只有满足可行顶和等于边权才能配对
女一:
第一轮
女一与男一:10 + 0 = 10,配对成功
女二:
第一轮:
女二和男一:40 + 0 != 20,配对失败
女二和男二:40 + 0 = 40,配对成功
女三:
第一轮:
女三和男二:110 + 0 = 110,但是男二与女二配对了,让女二调整,发现除了男二没有符合配对条件的,所以女三和男二配对失败,失败原因是,男二与女二配对了且女二不能调整。
女三和男三:110 + 0 != 30,配对失败
第一轮配对失败了,访问过的女生为女二、女三,访问过的男生为男二,男一,男三,男一至少需要调整 20 才能与女二配对成功,男三至少还需要调整 80 才能配对成功。所以 slack_min 等于 20。调整可行顶标,女二、女三减少 20,男三增加 30,如下图所示:
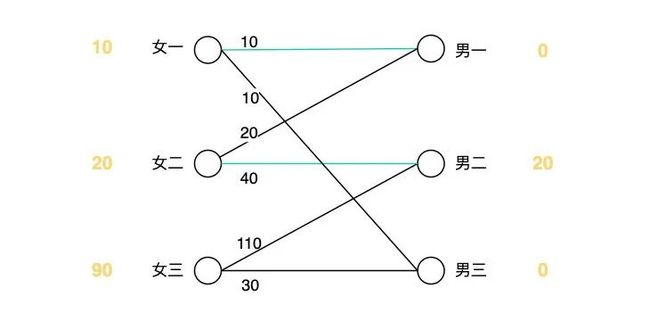
第二轮:
女三和男二:90 + 20 = 110, 但是男二和女二配对了,让女二尝试换对象,发现男一符合条件,但是男一已经和女一配对,尝试女一换对象,发现男三符合调整,所以此时女一换成了男三,女二换成男一,女三与男二配对,如图所示:
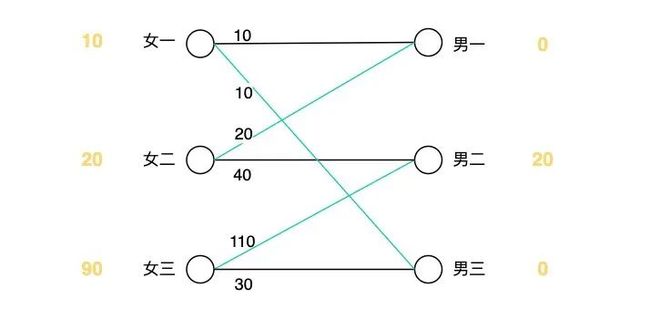
递归版本的代码:
#include
#include
#include
using namespace std;
const int MAXN = 305;
const int INF = 0x3f3f3f3f;
int love[MAXN][MAXN]; // 记录每个妹子和每个男生的好感度
int ex_girl[MAXN]; // 每个妹子的期望值
int ex_boy[MAXN]; // 每个男生的期望值
bool vis_girl[MAXN]; // 记录每一轮匹配匹配过的女生
bool vis_boy[MAXN]; // 记录每一轮匹配匹配过的男生
int match[MAXN]; // 记录每个男生匹配到的妹子 如果没有则为-1
int slack[MAXN]; // 记录每个汉子如果能被妹子倾心最少还需要多少期望值
int N;
bool dfs(int girl)
{
vis_girl[girl] = true;
for (int boy = 0; boy < N; ++boy) {
if (vis_boy[boy]) continue; // 每一轮匹配 每个男生只尝试一次
int gap = ex_girl[girl] + ex_boy[boy] - love[girl][boy];
if (gap == 0) { // 如果符合要求
vis_boy[boy] = true;
if (match[boy] == -1 || dfs( match[boy] )) { // 找到一个没有匹配的男生 或者该男生的妹子可以找到其他人
match[boy] = girl;
return true;
}
} else {
slack[boy] = min(slack[boy], gap); // slack 可以理解为该男生要得到女生的倾心 还需多少期望值 取最小值 备胎的样子【捂脸
}
}
return false;
}
int KM()
{
memset(match, -1, sizeof match); // 初始每个男生都没有匹配的女生
memset(ex_boy, 0, sizeof ex_boy); // 初始每个男生的期望值为0
// 每个女生的初始期望值是与她相连的男生最大的好感度
for (int i = 0; i < N; ++i) {
ex_girl[i] = love[i][0];
for (int j = 1; j < N; ++j) {
ex_girl[i] = max(ex_girl[i], love[i][j]);
}
}
// 尝试为每一个女生解决归宿问题
for (int i = 0; i < N; ++i) {
fill(slack, slack + N, INF); // 因为要取最小值 初始化为无穷大
while (1) {
// 为每个女生解决归宿问题的方法是 :如果找不到就降低期望值,直到找到为止
// 记录每轮匹配中男生女生是否被尝试匹配过
memset(vis_girl, false, sizeof vis_girl);
memset(vis_boy, false, sizeof vis_boy);
if (dfs(i)) break; // 找到归宿 退出
// 如果不能找到 就降低期望值
// 最小可降低的期望值
int d = INF;
for (int j = 0; j < N; ++j)
if (!vis_boy[j]) d = min(d, slack[j]);
for (int j = 0; j < N; ++j) {
// 所有访问过的女生降低期望值
if (vis_girl[j]) ex_girl[j] -= d;
// 所有访问过的男生增加期望值
if (vis_boy[j]) ex_boy[j] += d;
// 没有访问过的boy 因为girl们的期望值降低,距离得到女生倾心又进了一步!
else slack[j] -= d;
}
}
}
// 匹配完成 求出所有配对的好感度的和
int res = 0;
for (int i = 0; i < N; ++i)
res += love[ match[i] ][i];
return res;
}
int main()
{
while (~scanf("%d", &N)) {
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
scanf("%d", &love[i][j]);
printf("%d\n", KM());
}
return 0;
} 参考文档:
https://oi-wiki.org/graph/graph-matching/bigraph-weight-match/
https://www.cnblogs.com/wenruo/p/5264235.html