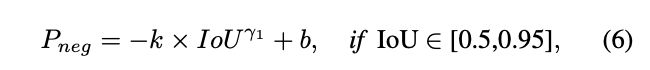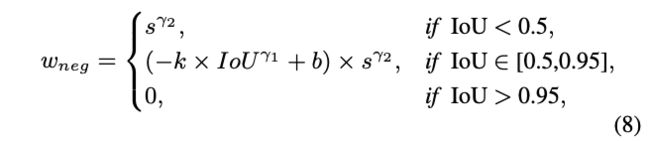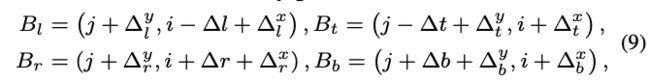论文提出自适应的label assignment方法DW,打破了以往耦合加权的惯例。根据不同角度的一致性和非一致性指标,动态地为anchor分配独立的pos权重和neg权重,可以更全面地监督训练。此外,论文还提出了新的预测框精调操作,在回归特征图上直接精调预测框
来源:晓飞的算法工程笔记 公众号
论文:A Dual Weighting Label Assignment Scheme for Object Detection
Introduction
Anchor作为目标检测器训练的基础单元,需要被赋予正确的分类标签和回归标签,这样的标签指定(LA, label assignment)过程也可认为是损失权重指定过程。对于单个anchor的cls损失计算,可以统一地表示为:
$w_{pos}$和$w_{neg}$为正向权重和反向权重,用于控制训练的方向。基于这个设计,可以将LA方法分为两个大类:
- Hard LA:每个anchor都可被分为pos或neg,即$w_{pos},w_{neg}\in \{0,1\}$以及$w_{pos}+w_{neg}=1$,这类方法的核心在于找到区分正负anchor的界限。经典的做法直接采用固定的IoU阈值进行判断,忽略了目标在大小和形状上的差异。而近期如ATSS等研究则提出动态阈值的概念,根据具体的IoU分布来划分anchor。但对于训练来说,不管是静态还是动态的Hard LA方法,都忽略了anchor本身的重要性差异。
- Soft LA:为了克服Hard LA的缺点,GFL和VFL等研究提出了soft权重的概念。这类方法基于IoU为每个anchor设定soft label目标,并且根据cls分数和reg分数为anchor计算$w_{pos}$和$w_{neg}$。但目前这些方法都专注于$w_{pos}$的设计,$w_{neg}$一般直接从$w_{pos}$中衍生而来,导致网络缺少来自于neg权重的监督信息。如图1所示,GFL和VFL为质量不同的anchor赋予相似的损失权重,这可能会降低检测器的性能。
为了给检测器提供更多的监督信息,论文提出了新的LA方法DW(dual weighting),从不同的角度单独计算$w_{pos}$和$w_{neg}$并让其能够互补。此外,为了给权重计算函数提供更准确的reg分数,论文还提出了新的bbox精调操作,预测目标的边界位置并根据对应的特征产生更准确的精调信息。
Proposed Method
Motivation and Framework
由于NMS的存在,检测器应该预测一致的bbox,既有高分类分数也有准确的位置定位。但如果在训练时平等地对待所有的训练样本,而cls分数越高的预测结果的reg位置不一定越准确,这往往会导致cls head与reg head之间就会存在不一致性。为此,Soft LA通过加权损失来更柔和地对待训练样本,加强cls head与reg head的一致性。基于Soft LA,anchor的损失可以表示为:
其中$s$为预测的cls分数。为一致性更高的预测结果分配更大的$w_{pos}$和$w_{reg}$,能够使得网络专注于学习高质量的预测结果,减轻cls head与reg head的不一致问题。
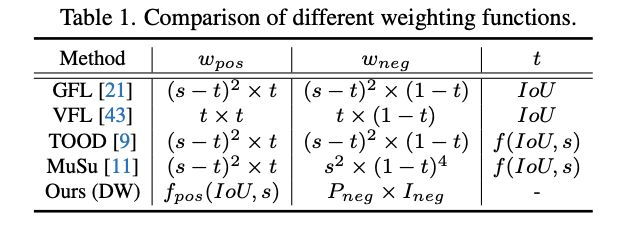
当前的方法直接将$w_{reg}$设置为$w_{pos}$,主要关注如何定义一致性以及如何将其集成到损失权重中。表1总结了一些方法对$w_{pos}$和$w_{neg}$的计算公式,这些方法先定义用于度量一致性的指标$t$,随后将$1-t$作为不一致性的度量指标,最后添加缩放因子将指标集成到损失权重中。
上述方法的$w_{pos}$和$w_{neg}$都是高度相关的,而论文认为pos和neg权重应该以prediction-aware的方式单独设置,具体如下:
- pos weighting function:以预测的cls分数和预测框的IoU作为输入,预测两者的一致性程度作为pos权重。
- neg weighting function:同样以预测cls分数和预测框的IoU作为输入,但将neg权重定义为anchor为负的概率以及anchor作为负的重要程度的乘积。
通过上述定义,对于pos权重相似的这种模棱两可的anchor,就可以根据不同的neg权重得到更细粒度的监督信息。
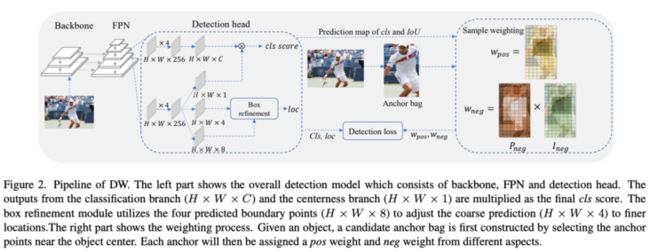
DW方法的整体流程如图2所示,先根据中心点距离来为每个GT构造候选正样本集,其余的anchor为候选负样本。由于负样本的统计信息十分混乱,所以不参与权重函数的计算。候选正样本会被赋予三个权重$W_{pos}$、$W_{neg}$以及$W_{reg}$,用于更有效地监督训练。
Positive Weighting Function
pos权重需要反映预测结果对检测性能的重要性,论文从目标检测的验证指标来分析影响重要性的因素。在测试时,通常会根据cls分数或cls分数与IoU的结合对单分类的预测结果进行排序,从前往后依次判断。正确的预测需满足以下两点:
- a. 与所属GT的IoU大于阈值$\theta$。
- b. 无其他排名靠前且所属GT相同的预测结果满足条件a。
上述条件可认为是选择高ranking分数以及高IoU的预测结果,也意味着满足这两个条件的预测结果有更大概率在测试阶段被选择。从这个角度来看,pos权重$w_{pos}$就应该与IoU和ranking分数正相关。首先定义一致性指标$t$,用于度量两个条件的对齐程度:
为了让不同anchor的pos权重的方差更大,添加指数调节因子:
最终,各anchor的pos权重会根据对应GT的候选anchor的pos权重之和进行归一化。
Negative Weighting Function
pos权重虽然可以使得一致的anchor同时具有高cls分数和高IoU,但无法区分不一致anchor的重要程度。如前面图1所示,anchor D定位校准但分类分数较低,而anchor B恰好相反。两者的一致性程度$t$一致,pos权重无法区分差异。为了给检测器提供更多的监督信息,准确地体现anchor的重要程度,论文提出为两者赋予更清晰的neg权重,具体由以下两部分构成。
Probability of being a Negative Sample
根据COCO的验证指标,IoU不满足阈值的预测结果一律归为错误的检测。所以,IoU是决定achor为负样本的概率的唯一因素,记为$P_{neg}$。由于COCO使用0.5-0.95的IoU阈值来计算AO,所以$P_{neg}$应该满足以下规则:
任意$[0.5,0.95]$上单调递减的函数都可以作为$P_{neg}$中间部分。为了简便,论文采用了以下函数:
公式6需要穿过点$(0.5,1)$和$(0.95, 0)$,一旦$\gamma_1$确定了,参数$k$和$b$可通过待定系数法确定。
图3展示了不同$\gamma_1$下的$P_{neg}$曲线。
Importance Conditioned on being a Negative Sample
在推理时,ranking队列中靠前的neg预测结果虽然不会影响召回率,但会降低准确率。为了得到更高的性能,应该尽可能地降低neg预测结果的ranking分数。所以在训练中,ranking分数较高的neg预测结果应该比ranking分数较低的预测结果更为重要。基于此,定义neg预测结果的重要程度$I_{neg}$为ranking分数的函数:
最终,整体的neg权重$w_{neg}=P_{neg}\times I_{neg}$变为:
$w_{neg}$与$IoU$负相关,与$s$正相关。对于pos权重相同的anchor,IoU更小的会有更大的neg权重。在兼容验证指标的同时,$w_{neg}$能给予检测器更多的监督信息。
Box Refinement
pos权重和neg权重都以IoU作为输入,更准确的IoU可以保证更高质量的训练样本,有助于学习更强的特征。为此,论文提出了新的box精调操作,基于预测的四条边的偏移值$O\in R^{H\times W\times 4}$进行下一步的精调。
考虑到目标边界上的点有更大的概率预测准确的位置,论文设计了可学习的预测模块,基于初步的bbox为每条边生成边界点。如图4所示,四个边界点的坐标定义为:
其中,$\{\Delta^x_l,\Delta^y_l,\Delta^x_t,\Delta^y_t,\Delta^x_r,\Delta^y_r,\Delta^x_b,\Delta^y_b\}$为精调模块的输出。最后,结合边界点的预测和精调模块的输出,最终精调后的anchor偏移$O^{'}$为:
Loss Function
DW策略可直接应用到大多数的dense检测器中。论文将DW应用到FCOS中并进行了少量修改,将centerness分支和分类分支合并成cls分数,网络的损失为:
这里的$\beta$跟公式3是同一个,$N$和$M$分别为候选anchor数和非候选anchor数。
Experiment
平衡超参数对性能的影响。
候选anchor选择方法对性能的影响。第一种为中心点的距离阈值,第二种选择最近的几个,第三种为距离权重与pos权重乘积排序。
neg权重计算方式对比。
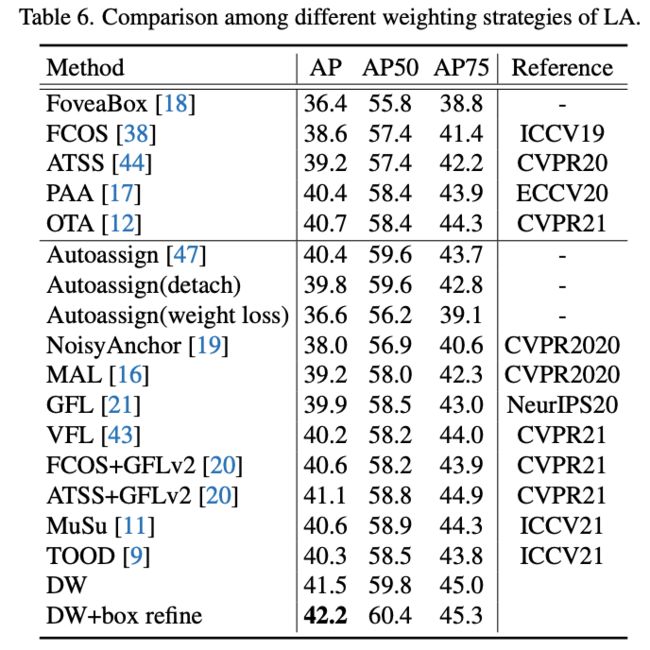
LA研究之间的对比。
与SOTA检测算法对比。
Conclusion
论文提出自适应的label assignment方法DW,打破了以往耦合加权的惯例。根据不同角度的一致性和非一致性指标,动态地为anchor分配独立的pos权重和neg权重,可以更全面地监督训练。此外,论文还提出了新的预测框精调操作,在回归特征图上直接精调预测框。
如果本文对你有帮助,麻烦点个赞或在看呗~
更多内容请关注 微信公众号【晓飞的算法工程笔记】