图深度学习——简单的图嵌入,图嵌入的通用框架和保留不同信息的图嵌入方法：DeepWalk，LINE，Node2vec，Struc2vec，模块度

图嵌入的通用框架

第一个部分
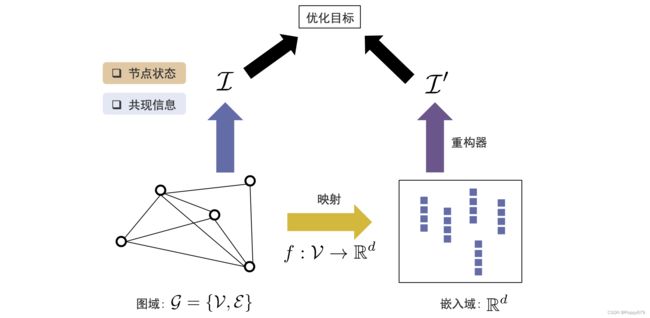
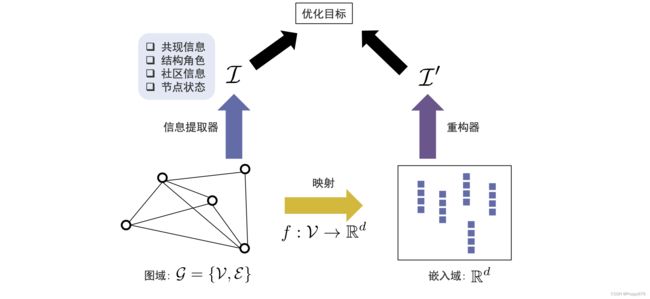
图数据可以看作有两种表示方法：图域（图的拓扑结构表示出来的图信息），嵌入域（向量空间表示出来的图信息）。
因此在通用框架中需要一个映射函数，映射函数可以把图上的每个节点从图域映射到嵌入域（高维 --> 低维）
第二个部分
在图域中需要有一个信息提取器，在图域中提取重要信息（共现信息、结构角色、社区信息和节点状态）。在嵌入域需要有一个重构器，在嵌入域基于每一个节点的表示，去重构信息，并且使得信息提取器提取信息和重构器重构信息尽可能接近。这样可以在嵌入域通过嵌入尽可能保留信息提取器提取到的信息。
以此实现图嵌入的通用框架。

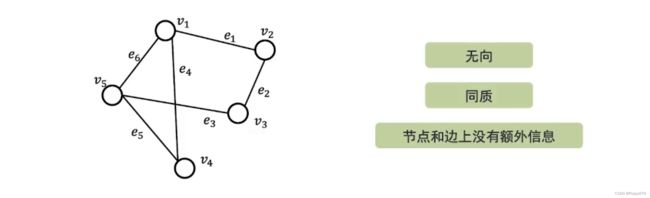
简单图

简单图是最简单的一种图的表示。

• 图是无向的，边是对称的。
• 图是同质的，只有一类节点和一类边。
• 节点和边上没有额外的信息（属性等）

简单图嵌入

保留邻域信息

保留共现信息的图嵌入：DeepWalk

word2vec：从文本中提取共现信息，在映射空间中去重建共现信息。通过提取得到的共现信息和重建的共现信息尽可能接近，以此学习到词的嵌入。
词嵌入–> 图嵌入
将词嵌入方法应用在图领域需要解决的问题：

1. 词嵌入学习学的是词的嵌入表示，那么在图中对应学习的是什么？
2. 词通过词之间的序列来表示一句话，段落等，自然可知其中的共现信息，那么在图中的节点之间没有顺序，怎么知道节点的共现信息（如何提取图的共现信息？通过边？）

DeepWalk的思想：
把每一个节点看作是一个词。词在语料之间存在序列（顺序），节点在图中不存在序列，所以通过随机游走来产生很多的途径。

每一个途径就相当于一个词的序列，这样以来就将图类别成语料，把Word2vec方法引入到图上。

DeepWalk：基于通用框架分析

映射函数

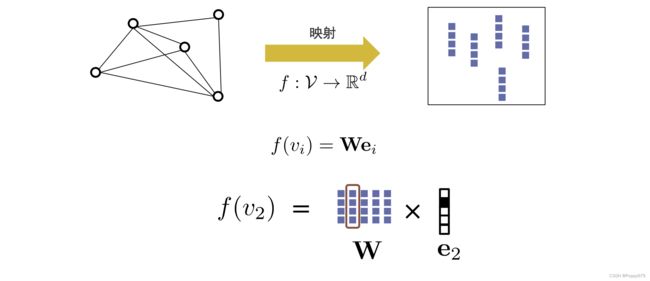
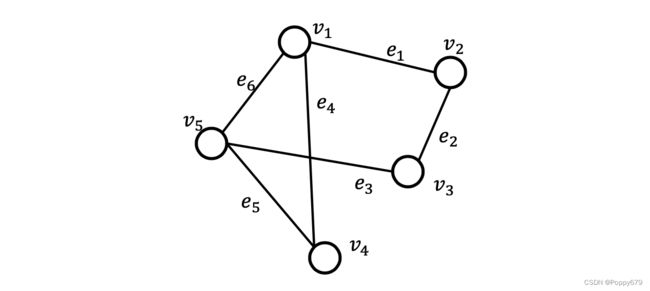
如图所示，$W$ 中的每一列表示图上节点的嵌入。映射函数公式：

$f\left(v_i\right)={\mathbf{W}\mathbf{e}}_i$

$e_i$ 就是一个onehot向量，$e_i$ 中维度大小和节点个数相同。例：
$W$ 与 $e_2$ 相乘，就能将其对应的嵌入表示提取出来$f\left(v_2\right)$。

随机游走

DeepWalk通过随机游走产生节点的序列。节点的序列就对应着word2vec中词的句子序列。

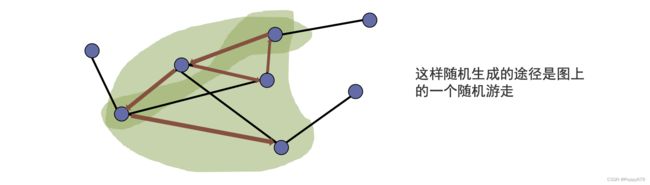
随机游走方式：随机游走在点 $v^{(t)}$ 根据如下均匀分布选择下一个节点：

$p\left(v^{(t+1)}\mid v^{(t)}\right)=\{\begin{array}{ll}\frac{1}{d\left(v^{(t)}\right),},& \text{ if }{v}^{(t+1)}\in \mathcal{N}\left(v^{(t)}\right)\\ 0,& \text{ otherwise }\end{array}$

如果下一个节点是当前节点的邻居，那么会以相同的概率游走到其邻居上。$d(v^{(t)})$ 表示当前节点的度。即如图所示，红色节点有4个邻居，那么红色节点会以1/4的概率随机游走到下一个节点（当前节点的邻居节点）。这样就会生成一个途径，就相当于Word2vec中的语句序列。

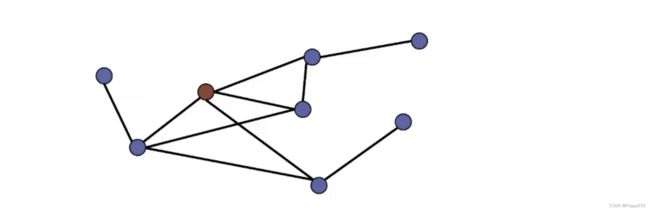
基于随机游走的信息提取器

基于随机游走产生途径后，就可以基于途径提取节点之间的共现信息。

首先将一个途径中的每个节点看作是两种角色：中心节点和上下文节点。
那么就定义上下文节点是中心节点一定距离内的点。假设这里定义上下文节点是中心节点距离为2的节点，那么就可以得到如下所示的中心节点和上下文节点。

得到中心节点和上下文节点以后，就可以将节点对作为共现信息，表示为

${\mathcal{I}}_{\mathcal{W}}=\left\{\left(v_{cen},v_{con}\right)\right\}$

中心节点和上下文节点是在同一个途径、一定大小窗口中共现了的节点对。$v_{cen}$ 表示中心节点， $v_{con}$ 表示上下文节点。通常情况下，会从每个节点出发，重复多次随机游走。通过多次随机游走得到节点和节点之间的共现信息 $\mathcal{W}=\left(v^{(1)},\dots ,v^{(6)}\right)$，所有共现信息 $\mathcal{R}=\{\mathcal{W}\}$ 的节点对集合用 $\mathcal{I}$ 表示。

$\mathcal{I}={\bigcup }_{\mathcal{W}\in \mathcal{R}}{\mathcal{I}}_{\mathcal{W}}$

重构器

上图左边表示图域中提取出来的共现信息，在嵌入域中如何重构节点对？

通过给定一个中心节点，来预测其上下文节点的概率 $p\left(v_{con}\mid v_{cen}\right)$，然后计算同一途径上所有的节点对概率：

${\prod }_{\left(v_{\text{cen }},v_{con}\right)\in {\mathcal{I}}_{\mathcal{W}}}p\left(v_{\text{con }}\mid v_{cen}\right)$

因为是多次随机游走得到的共现信息，因此也要对所有途径上的节点对集合进行计算共现信息的概率。

${\prod }_{\mathcal{W}\in \mathcal{R}}{\prod }_{\left(v_{cen},v_{con}\right)\in {\mathcal{I}}_{\mathcal{W}}}p\left(v_{con}\mid v_{cen}\right)$

以上公式计算所有从图域中抽取出来的共现节点对的概率。

在DeepWalk中，实际上是使用了两个映射函数。因为在图域中，每个节点既可以是中心节点，又可以是上下文节点。且中心节点和上下文节点的嵌入是不同的。

$\begin{array}{rl}{f}_{cen}\left(v_i\right)& ={\mathbf{W}}_{cen}{\mathbf{e}}_i\\ f_{con}\left(v_i\right)& ={\mathbf{W}}_{con}{\mathbf{e}}_i\end{array}$

那么如何在给定一个中心节点，去重构它的共现信息？

通过给定一个中心节点去预测他的上下文节点的概率。这里的概率是通过一个softmax function来给出：

$P=\frac{\exp \left(f_{\text{con }}{\left(v_{\text{con }}\right)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}{{\sum }_{v\in \mathcal{V}}\exp \left(f_{\text{con }}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}$

中心节点的嵌入和上下文节点的嵌入做内积（？），一定程度上反映了节点嵌入的相似性的。如果嵌入是规则化的，那么它的内积就表示余弦相似度。分子是中心节点嵌入和上下文节点嵌入之间的相似性，分母是其他任何节点和这个中心节点及其上下文节点嵌入的相似性之和。

一个softmax函数放在其嵌入内积上，可以得到在给定一个中心节点，相对其他节点它的概率值。

目标函数

如何让重构信息和共现信息尽可能的接近

目的就是尽可能将共现信息中的值在重构中预测准确。即，给定中心节点，让重构共现信息的值预测准确的概率最大化。（类似统计学中的最大似然估计：最大化观察到的数据的概率）

最大似然估计的思想在于，对于给定的观测数据 $x$，我们希望能从所有的参数 ${\theta }_1,{\theta }_2,\cdots ,{\theta }_n$ 中找出能最大概率生成观测数据的参数 ${\theta }^{\ast }$作为估计结果。

最大化观察到的数据的概率：

${\prod }_{\mathcal{W}\in \mathcal{R}}{\prod }_{(v_{\text{cen },v_{\text{con }})\in {\mathcal{I}}_w}}\frac{\exp \left(f_{\text{con }}{\left(v_{\text{con }}\right)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}{{\sum }_{v\in \mathcal{V}}\exp \left(f_{\text{con }}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}$

对公式进行转换，将乘积问题转换成求和问题（优化计算复杂度）、最大化问题转换成最小化问题：

$min:-{\sum }_{\mathcal{W}\in \mathcal{R}}{\sum }_{\left(v_{\text{cen }},v_{\text{con }}\right)\in {\mathcal{I}}_{\mathcal{W}}}\log \frac{\exp \left(f_{\text{con }}{\left(v_{\text{con }}\right)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}{{\sum }_{v\in \mathcal{V}}\exp \left(f_{\text{con }}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}$

总结一下就是通过计算，将随机游走得到的共现信息中的节点对出现的概率最大化，以此提高重构共现信息的预测准确度。（也不知道总结的对不对）

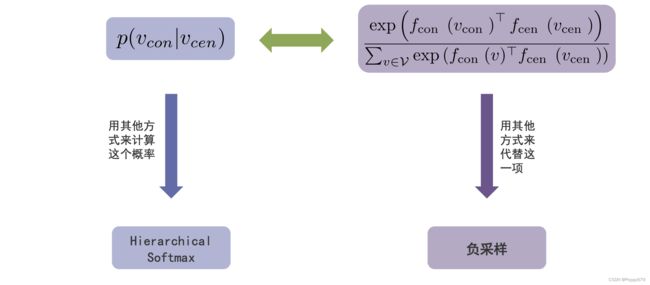
计算问题 给定一个中心节点，计算其上下文节点概率时，需要对所有节点的节点对内积进行求和，这个过程耗费计算资源和时间。

${\sum }_{v\in \mathcal{V}}\exp \left(f_{\mathrm{con}}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)$

如何提高扩展性？

两种思路：
1.其他方法计算概率：Hierarchical Softmax（层次softmax）

2.其他的方法达到同样的目的：负采样

Hierarchical Softmax

进行查找的时候，节点的个数相当于字典的维度，在平级softmax中要想知道概率就需要计算每一个节点之间的概率。要计算一个中心节点与其上下文节点之间节点对的概率，就要从第一个节点开始逐一搜索进行计算。层级softmax可以通过二分索引加速计算。

参考：Hierarchical Softmax

在进行最优化的求解过程中：从隐藏层到输出的Softmax层的计算量很大，因为要计算所有词的Softmax概率，再去找概率最大的值。

层级softmax的二分索引中，所有的叶子节点都是图上的节点。那么计算给定中心节点和其它节点的概率就转换成在索引树上找到一条路径。
进一步假设，每一条路径都是独立的，将计算可以进一步简化，层次softmax将计算中心节点和其他节点的概率问题变换成一系列二分类问题（如何从根节点找到叶子节点）。

如何计算一个节点到达另一个节点的二分类概率：

$p($ left $\mid b_0,v_8)=\sigma \left(f_b{\left(b_0\right)}^{\top }f\left(v_8\right)\right)$

$\sigma (\cdot )$ 就是sigmoid函数。这里的分层softmax就是一个查找问题，查找问题的每一步就是一个二分类问题。

和之前的softmax相比，层次softmax还能对每一个内部节点的表示进行映射，提高了效率。

负采样

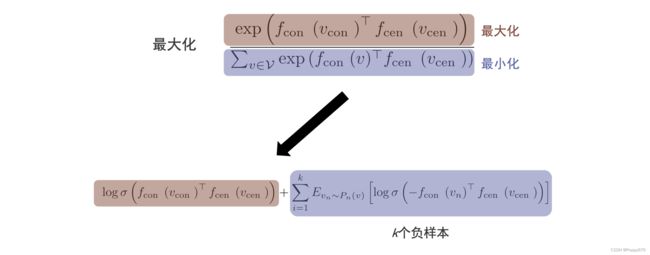
最大化： $\frac{\exp \left(f_{\text{con }}{\left(v_{\text{con }}\right)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}{{\sum }_{v\in \mathcal{V}}\exp \left(f_{\text{con }}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)}$

等价于使分子 $\exp \left(f_{\mathrm{con}}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)$ 最大化，使分母 ${\sum }_{v\in \mathcal{V}}\exp \left(f_{\mathrm{con}}(v{)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)$ 最小化。

通过负采样的方式去实现这样的目标。上述公式可以等价转换成：

$\log \sigma \left(f_{\text{con }}{\left(v_{\text{con }}\right)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)+{\sum }_{i=1}^k{E}_{v_n\sim P_n(v)}\left[\log \sigma \left(-f_{\text{con }}{\left(v_n\right)}^{\top }{f}_{\text{cen }}\left(v_{\text{cen }}\right)\right)\right]$

最小化采取负采样的方式来实现，采样 $k$ 个没有出现在中心节点的节点对作为负样本，最大化正样本的概率，最小化负样本的概率。

其他保留共现信息的图嵌入方法

LINE

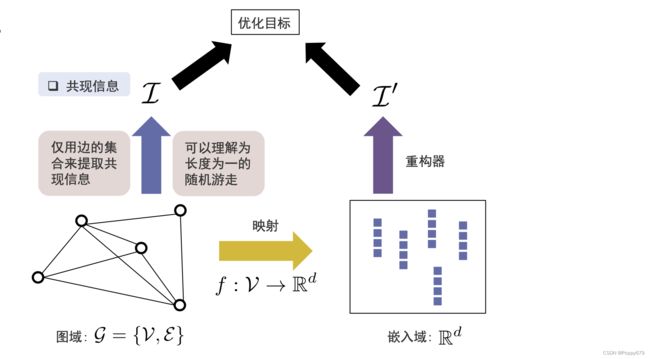
在DeepWalk中通过随机游走的方式产生共现信息，LINE用边的集合来提取共现信息，类比DeepWalk就是一种长度为1的随机游走。其他部分和DeepWalk类似。

Node2vec

在DeepWalk中的随机游走是一阶随机游走，即从一个节点游走到另一个节点时，与其它节点是无关的。Node2vec中的二阶游走，除了考虑当前节点的信息还要考虑上一个节点的信息，更灵活的探索节点的邻域信息。

二阶随机游走

当前节点决定下一个节点要游走到哪一个节点。在DeepWalk中，只考虑了邻域，当前节点以相同的概率游走到它的邻域。在二阶随机游走选择下一个节点时，除了考虑当前节点，还会考虑上一个节点。会以 $\frac{1}{p}$ 的概率往回游走。其他节点会考虑上一个节点与之的距离，比如当上一个节点与下一个节点的距离为$q>1$时， 会倾向于游走到距离上一个节点更近的节点；当上一个节点与下一个节点的距离为$q<1$时，就尽可能的想远离这个节点 $\frac{1}{q}$。

${\alpha }_{pq}\left(v^{(t+1)}\mid v^{(t-1)},v^{(t)}\right)=\{\begin{array}{ll}\frac{1}{p},& \mathrm{dis}\left(v^{(t-1)},v^{(t+1)}\right)=0\\ 1,& \mathrm{dis}\left(v^{(t-1)},v^{(t+1)}\right)=1\\ \frac{1}{q},& \mathrm{dis}\left(v^{(t-1)},v^{(t+1)}\right)=2\end{array}$

参考：探索node2vec同质性和结构性之谜

$p$ 值大，倾向不回溯，降低2-hop的冗余度;
$p$ 值小，倾向回溯，采样序列集中在起始点附近；
$q>1$, BFS-behavior, local view;
$q<1$, DFS-behavior.

通过p和q两个参数就可以调整游走的策略从而实现深度优先搜索（DFS）和广度优先搜索（BFS），DFS擅长学习网络的同质性，BFS擅长学习网络的结构性；

以上模型都基于图嵌入的通用框架，在产生序列的方法上存在差别。

保留结构角色

结构角色

在前面介绍的方法中，两个嵌入要接近，必须是原图节点要经常共现，即这些节点在图上的距离是非常接近的。但是在实际应用中，共现信息并不是所需要的信息，反而结构角色信息更加重要。

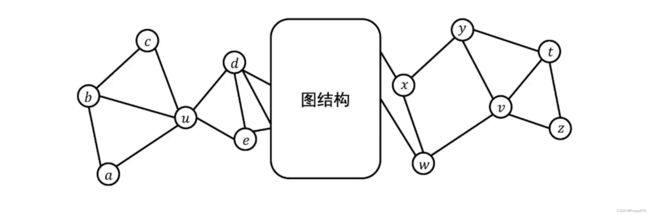
例如，如图所示 $u$ 和 $v$ 两个节点在图中距离是比较远的，因此它们共现的概率是很小的，换句话说就是两个节点的嵌入是不接近的，两个节点是不相似的。但是从结构上看，$u$ 和 $v$ 的拓扑结构是非常类似的，因此可以说在图中，$u$ 和 $v$ 的结构角色是相似的。（现实生活中，高铁枢纽站之间是相隔很远的，但它们的角色是相似的，都是交通枢纽作用）如果仅仅以共现来判断，是无法捕捉到重要信息，因此需要为这样的图/应用保留结构角色信息，提供保留结构角色信息的嵌入方法。

保留结构角色信息的图嵌入：struc2vec

经过结构相似性的重新图构建，得到的新图的关系不再表示距离，而是表示结构角色的相似性。然后再利用DeepWalk类似的方法去得到节点嵌入。在这个节点嵌入中包含节点的结构角色信息。

如何衡量角色结构相似性，如何利用角色结构相似性来构建反映结构角色信息的新图？

衡量角色结构相似性

通过度相似来衡量。
给定节点 $u$ 和 $v$，他们的距离 $dist(d_u^0,d_v^0)$ （就是两节点的0阶角色相似性），此外还要考虑高阶信息——邻居节点的度相似。这里的一阶信息来自邻居节点的度信息，根据度的大小排序，距离表示$dist(S_u^1,S_v^1)$ ，$S_u^1)$ 表示节点 $u$ 的邻居的度的序列。以此类推，去获得 $k$ 阶（高阶）邻居的度相似，$dist(S_u^k,S_v^k)$ 。这样以来，给定节点对，可以得到从0阶到 $k$ 阶邻居的度的相似性，通过度相似来衡量角色结构相似性。

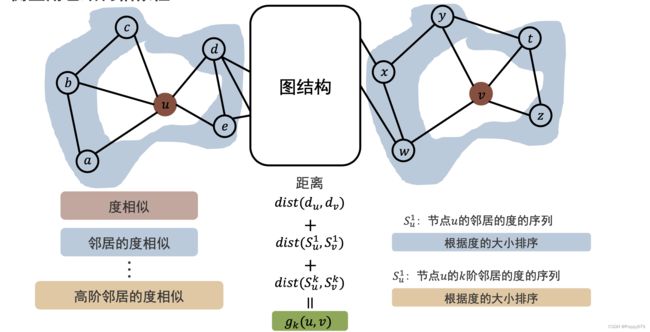
有了度相似性后，如何去构建反映角色结构相似性的新图？

那么总的相似性就是前面所有度相似的和：

$g_k(u,v)=dist(d_u^0,d_v^0)+dist(S_u^1,S_v^1)+...+dist(S_u^k,S_v^k)$

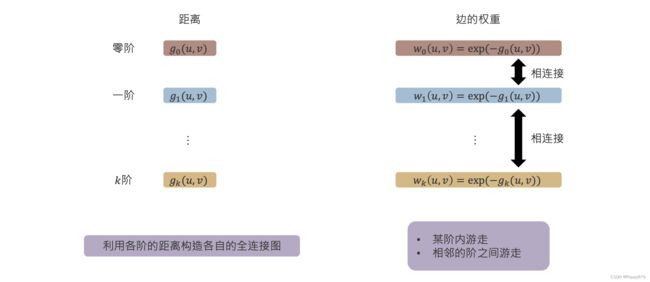
全连接图的构造

对于每一阶都构造一个图：利用各阶的距离构造各自的全连接图。

构建新图的边的权重与每阶度相似性有关：$w_k(u,v)=\exp \left(-g_k(u,v)\right)$

每一阶都构造一个结构角色相似性的全连接图，同时各阶之间的节点通过权重（与相似性相关）对应连接起来。因此可以看到，这个是一个 $k$ 层的图。在这样 $k$ 阶的图以后，就可以定义在图上的随机游走：

1. 某阶内随机游走
2. 相邻的阶之间游走

之后就可以通过DeepWalk来学习节点嵌入表示。

保留节点状态

节点状态

节点中心性：用于衡量节点在图上的重要程度。给定一个社交网络，有的用户是比较重要的用户，有的是普通用户。在一些任务中，需要保留这样的节点信息（比如想要对图上节点进行排序时，需要保留节点状态信息）

保留节点状态

首先和DeepWalk类似会保留节点的共现信息，此外还要保留节点的状态信息。同时在重构器重构信息时，也是重构共现信息和节点状态信息。共现信息的提取和重构和DeepWalk是一样的，所以重点关注在提取节点状态信息和重构节点状态信息，以及如何让这两部分信息通过优化目标尽可能的接近。

信息提取器

通过节点中心度来计算节点状态，想要保留的信息是节点状态的一个序列（排序）：$\left(v(1),\dots ,v_{(N)}\right)$，这里的节点序列表示的是根据状态的排序。

计算节点中心度得到的是分数，为什么不直接保留计算得到的分数，而是给节点按照节点状态排序，保留这样的排序序列？

1. 使用不同节点中心度计算方法得到的节点中心度分数是不一样的，但是序列是相对更稳定的。
2. 不同节点状态信息的衡量方法是不一样的，因此分数大小可能因为不同衡量方法而完全不一样。
3. 对于某一些节点状态，它们的分数是非常接近的，这对后续建模是不利的。

重构器

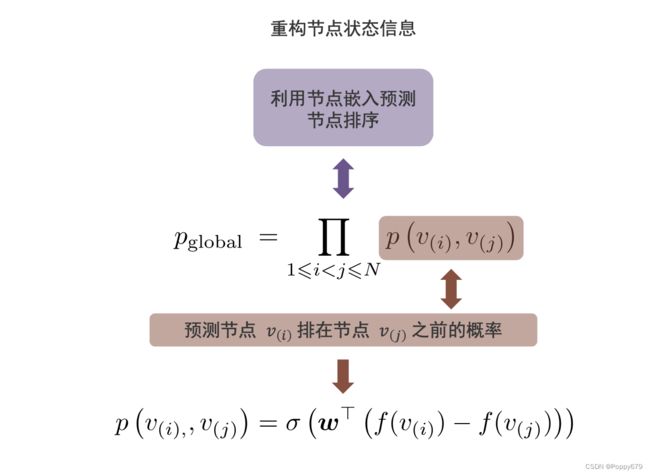
给定节点 $i$ 和 $j$ 的节点对，那么这两个节点在节点状态信息序列中一定存在一个先后顺序。假设 $i$ 在 $j$ 的前面，那么想要在所有节点对中去预测节点 $v_{(i)}$ 排在 $v_{(j)}$ 之前的概率，然后在重构器中去重构 $i$ 和 $j$ 的状态信息。那么如何对概率进行建模？
在DeepWalk中，通过两个输入的概率的softmax来计算概率。这里使用softmax，会导致 $v_{(i)}$ 和 $v_{(j)}$，$v_{(j)}$ 和 $v_{(i)}$ 是一样的，并不能区分 $v_{(i)}$ 和 $v_{(j)}$ 的序列顺序问题，所以提出方法：

$p\left(v_{(i),},v_{(j)}\right)=\sigma \left({\mathbf{w}}^{\top }\left(f\left(v_{(i)}\right)-f\left(v_{(j)}\right)\right)\right)$

通过排在前面的概率的嵌入减去排在后面的概率的嵌入，再通过一个线性的映射，最后通过sigmoid函数得到它们的概率。这其中减号的引入能够区分节点状态信息的顺序。

目标函数

目标函数和之前是一样的，最大化两个节点对抽取出来的节点序列中的相对信息，就是要尽可能将抽取出来的节点对的顺序预测正确：通过最大化它们之间的概率。

$p_{\text{global }}={\prod }_{1⩽i<j⩽N}p\left(v_{(i)},v_{(j)}\right)$

通常情况下，对上式进行转换，转换成最小化它的对数的相反数。

保留社区结构

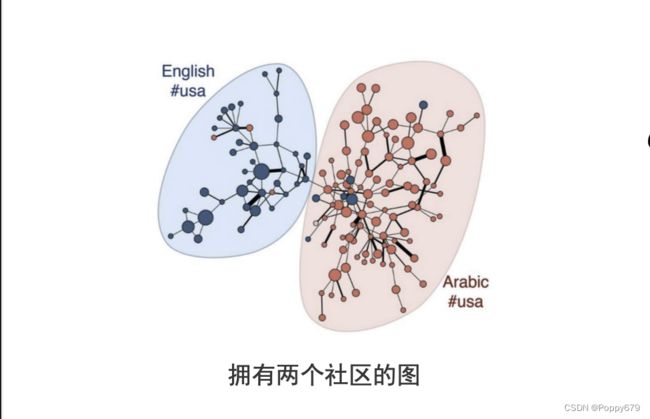
如图所示，节点和节点之间不是随机连接的，节点和节点间可能存在社区。在社区中，社区内部连接是紧密的；社区和社区之间连接不紧密（跨社区的连接是不紧密的）。（社区发现）当社区信息对于任务是有用时，就需要对图嵌入进行设计，保留社区结构。

基于模块度的社区发现

流行的社区发现方法：基于模块度的方法
模块度：

$Q=\frac{1}{2\cdot \mathrm{vol}(\mathcal{G})}{\sum }_{ij}\left({\mathbf{A}}_{i,j}-\frac{\mathrm{d}\left(v_i\right)\mathrm{d}\left(v_j\right)}{\mathrm{vol}(\mathcal{G})}\right)h_i{h}_j$

最大化模块度来实现社区发现。

${\mathbf{A}}_{i,j}$ 表示邻接矩阵，$d(v_i)$ 表示节点的度，$\mathrm{vol}(\mathcal{G})$ 表示所有节点的度的总和，$h_i$ 表示节点所属社区的指示函数，取值0或者1
$\frac{1}{2\cdot \mathrm{vol}(\mathcal{G})}$ 是一个规则化项，$\frac{\mathrm{d}\left(v_i\right)\mathrm{d}\left(v_j\right)}{\mathrm{vol}(\mathcal{G})}$ 表示节点 $v_i$ 和 $v_j$ 在保持节点原有度的情况下，它们之间出现一条边的概率期望值。

在两个社区的情况下，$h_i=1$ 表示社区1，$h_i=-1$ 表示社区2（表示节点$v_i$属于哪个社区） 在模块度公式里，$h_i$ 的值是未知的，社区发现的目的就是为了得到这个值。公式可以简化成如下形式：

$Q=\frac{1}{2\cdot \mathrm{vol}(\mathcal{G})}{\mathbf{h}}^{\top }\mathbf{B}\mathbf{h}$， 其中${\mathbf{B}}_{i,j}$ 就是 ${\mathbf{A}}_{i,j}-\frac{\mathrm{d}\left(v_i\right)\mathrm{d}\left(v_j\right)}{\mathrm{vol}(\mathcal{G})}$

节点 $v_i$ 和 $v_j$ 在同一个社区的时候，他们之间的连接很紧密，观测值会比期望值更大；节点 $v_i$ 和 $v_j$ 在不同社区的时候，他们之间的连接不紧密，观测值会比期望更小。

也就是说当随机期望的值比较大的时候，说明两个节点间有连接的趋势。将观测到的可能性比期望值大的放在同一个社区。

拓展到多个社区的情况

在多个社区的情况下，不能仅仅用0/1来表示社区，所以用矩阵来表示社区。矩阵的每一行都是onehot向量，假设有 $k$ 个社区，那么每一行向量的维度为 $k$。

保留社区结构的图嵌入

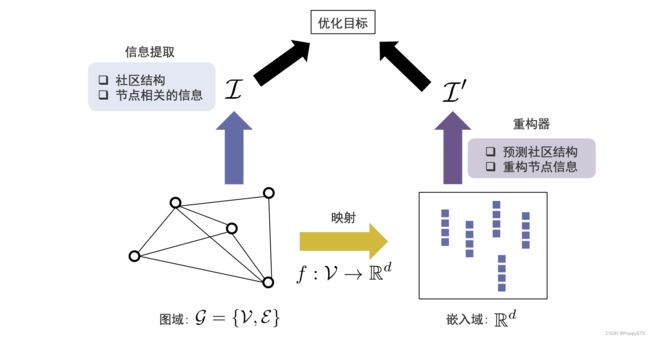
在保留社区结构的图嵌入中，信息提取阶段提取1.社区结构2.节点相关信息；同时重构器1.预测社区结构2.重构节点信息。

提取节点相关信息

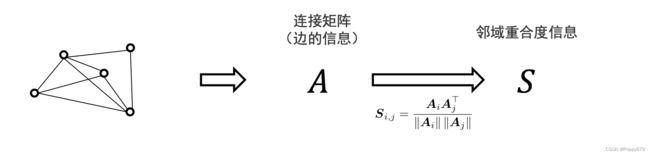
在信息提取阶段，除了保留图的邻接矩阵（一阶信息），还会考虑邻域重合度信息（二阶信息），即节点 $i$ 和节点 $j$ 之间的邻域相似性：
${\mathbf{S}}_{i,j}=\frac{{\mathbf{A}}_i{\mathbf{A}}_j^{\top }}{\Vert {\mathbf{A}}_i\Vert \Vert {\mathbf{A}}_j\Vert }$ 。 用 $\eta$ 参数将一阶信息和二阶信息聚合起来： $P=A+\eta \cdot S$

重构器和目标函数

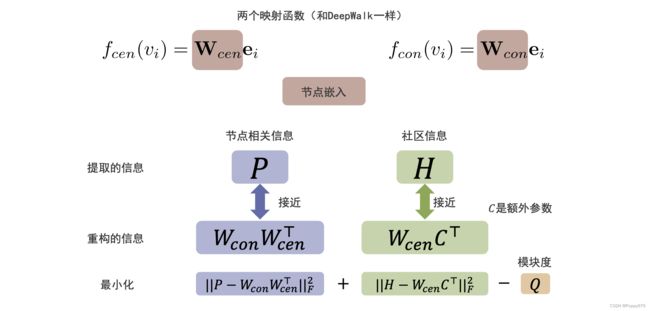
在这个模型中和DeepWalk类似，有两个映射函数：

$f_{cen}\left(v_i\right)={\mathbf{W}}_{cen}{\mathbf{e}}_i$
$f_{con}\left(v_i\right)={\mathbf{W}}_{con}{\mathbf{e}}_i$

节点相关信息就是两两节点的相关信息，通过中心节点和上下文节点的嵌入存储信息；方法通过公式表示： ${\Vert P-W_{\text{con }}{W}_{cen}^{\top }\Vert }_F^2$ 其中 $P$ 是一个矩阵，然后对其做一个矩阵分解，这里就是一个低秩矩阵分解。

社区信息的重构是中心节点的嵌入通过一个映射函数映射到社区信息上去。方法通过公式表示：$\Vert H-W_{cen}{C}^{\top }\Vert {\Vert }_F^2$

此外在目标函数中还要包含最大化的模块度 $Q$。通过这样的目标函数，可以保留原来节点的相关信息，也可以保留社区信息。这就是基于保留社区结构的图嵌入方法。
最小化目标函数：

${\Vert P-W_{\text{con }}{W}_{cen}^{\top }\Vert }_F^2+\Vert H-W_{cen}{C}^{\top }\Vert {\Vert }_F^2-Q$