PyTorch学习笔记【3】:使用神经网络拟合数据
提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- 1. 神经网络
-
- 1.1. 组成一个多层网络
- 1.2. 理解误差函数
- 1.3. 激活函数
- 1.4. 选择最佳的激活函数
- 1.5. 更多激活函数
- 2. PyTorch nn 模块
-
- 2.1. 线性模型
-
- 2.1.1. 批量输入
- 2.1.2. 优化批次
- 3. 完成一个神经网络
-
- 3.1. 替换线性模型
- 3.2. 检查参数
- 3.2. 与线性模型对比
- 总结
前言
本文是基于《Pytorch深度学习实战》一书第六章的内容所整理的学习笔记
相关代码的解释以及对应的拓展。
本文使用的代码均基于jupyter
1. 神经网络
深度学习的核心是神经网络:一种能够通过简单函数的组合来表示复杂函数的数学实体
这些复杂函数的基本构件是神经元,其核心就是输入的线性变换然后应用一个固定的非线性函数,即激活函数。
从数学上将,我们可以把它写成 o = f(wx+b),其中x是输入,w是权重或比例因子,b是偏置或偏移量,f是激活函数。通常,x和o可以是简单的标量,或向量值,w可以是单个标量或矩阵,而b是标量或向量。在后一种情况下,前面的表达式被称为一层神经元。
1.1. 组成一个多层网络
1.2. 理解误差函数
我们之前的线性模型和我们将实际用于深度学习的模型之间的一个重要区别是误差函数的形状。我们的线性模型和误差平方损失函数有一条凸误差曲线,它有一个奇异的、明确定义的最小值。如果采用其他方法,则可以自动、确定地求出使误差函数的值最小的参数,这意味着我们的参数更新试图尽可能估计那个奇异的正确答案。
即使使用相同的误差平方损失函数,神经网络也不具有与凸误差曲面相同的特性!对于我们试图近似的每一个参数,都没有单一的正确答案。相反,我们试图让所有的参数,当协同作用时,产生一个有用的输出。由于这个有用的输出只是接近事实,所以会有一定程度的不完美。
1.3. 激活函数
激活函数的2个重要作用:
- 在模型的内部,它允许输出函数在不同的值上有不同的斜率,这是线性函数无法做到的。通过巧妙地为许多输出设置不同的斜率,神经网络可以近似任意函数
- 在网络的最后一层,它的作用是将前面的线性运算的输出集中到给定的范围内
- 限制输出范围
对输出值设置上线
torch.nn.Hardtanh() - 压缩输出范围
torch.nn.Sigmoid()
这些函数的曲线在x趋于负无穷大时逐渐接近0或-1,随着x逐渐接近1,函数在x==0时具有基本恒定的斜率
- 限制输出范围
1.4. 选择最佳的激活函数
激活函数有如下特性:
- 激活函数是非线性的
- 激活函数是可微的,因此可以通过他们计算梯度
函数的真实情况:
- 它们至少有一个敏感范围,在这个范围内,对输入的变化会导致输出产生相应的变化
- 它们包含许多不敏感(或饱和)的范围,即输入的变化导致输出的变化很小或没有变化。
通常情况下,激活函数至少有以下一种特征
- 当输入到负无穷大时,接近(或满足)一个下限
- 正无穷时相似但上界相反
组成的强大机制:
在—个由线性+激活单元构成的网络中,当不同的输入呈现给网络时,不同的单元会对相同的输入在不同范围内响应;与这些输入相关的错误将主要影响在敏感区域工作的神经元,使其他单元不受学习过程的影响。此外,由于在敏感范围内,激活对其输入的导数通常接近于1,因此通过梯度下降估计在该范围内运行的单元的线性变换参数将与我们之前看到的线性拟合非常相似。
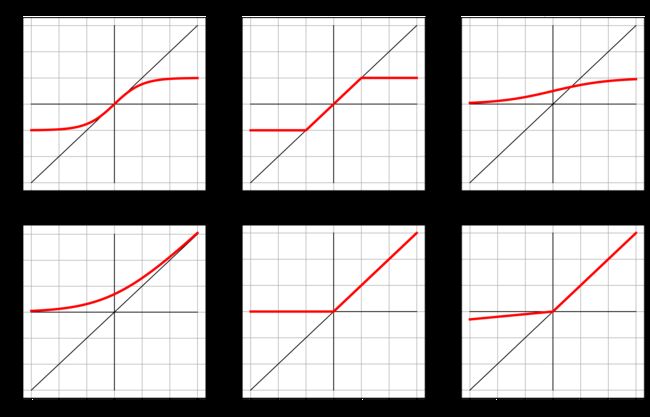
1.5. 更多激活函数
2. PyTorch nn 模块
PyTorch有一个专门用于神经网络的子模块,叫做torch.nn,它包含创建各种神经网络结构所需的构建块,这样的构建块通常称为层。一个模块可以有一个或多个参数实例作为属性,这些参数实例是张量,它们的值在训练过程中得到了优化。一个模块还可以有一个或多个子模块作为属性,并且还能够追踪到它们的参数。
%matplotlib inline
import numpy as np
import torch
import torch.optim as optim
torch.set_printoptions(edgeitems=2, linewidth=75)
t_c = [0.5, 14.0, 15.0, 28.0, 11.0, 8.0, 3.0, -4.0, 6.0, 13.0, 21.0]
t_u = [35.7, 55.9, 58.2, 81.9, 56.3, 48.9, 33.9, 21.8, 48.4, 60.4, 68.4]
t_c = torch.tensor(t_c).unsqueeze(1)
t_u = torch.tensor(t_u).unsqueeze(1)
t_u.shape
n_samples = t_u.shape[0]
n_val = int(0.2 * n_samples)
shuffled_indices = torch.randperm(n_samples)
train_indices = shuffled_indices[:-n_val]
val_indices = shuffled_indices[-n_val:]
train_indices, val_indices
t_u_train = t_u[train_indices]
t_c_train = t_c[train_indices]
t_u_val = t_u[val_indices]
t_c_val = t_c[val_indices]
t_un_train = 0.1 * t_u_train
t_un_val = 0.1 * t_u_val
2.1. 线性模型
构造函数n n.Linear接收3个参数:输入特征的数量,输出特征的数量,以及线性模型是否包含偏置(默认为True)
import torch.nn as nn
linear_model = nn.Linear(1, 1)
linear_model(t_un_val)
一个输入和一个输出特征,这只需要一个权重和一个偏置
linear_model.weight
linear_model.bias
x = torch.ones(1)
linear_model(x)
2.1.1. 批量输入
创建一个大小为BxNin的输入张量,其中B是批次的大小,Nin为输入特征的数量
x = torch.ones(10, 1)
linear_model(x)
2.1.2. 优化批次
进行批处理的原因:
- 充分利用并行的计算单元
- 一些高级模型使用来自整个批处理的统计信息,并且随着批处理大小的增加,这些统计系信息会变得更好
linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(
linear_model.parameters(), # 此方法替换params
lr=1e-2)
可以使用parameters()方法来访问任何nn.Module或它的子模块拥有的参数列表
linear_model.parameters()
list(linear_model.parameters())
此调用会递归到模块的构造函数__init__,并返回遇到的所有参数的简单列表。
优化器提供了一个用 requires_ grad=True 定义的张量列表,所有参数都是这样定义的,因为它们需要通过梯度下降进行优化。在调用 training_oss.backward()时,grad 在图的叶节点上累加,叶节点正是传递给优化器的参数。
def loss_fn(t_p, t_c):
squared_diffs = (t_p - t_c)**2
return squared_diffs.mean()
def training_loop(n_epochs, optimizer, model, loss_fn, t_u_train, t_u_val,
t_c_train, t_c_val):
for epoch in range(1, n_epochs + 1):
t_p_train = model(t_u_train)
loss_train = loss_fn(t_p_train, t_c_train)
t_p_val = model(t_u_val)
loss_val = loss_fn(t_p_val, t_c_val)
optimizer.zero_grad()
loss_train.backward()
optimizer.step()
if epoch == 1 or epoch % 1000 == 0:
print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"
f" Validation loss {loss_val.item():.4f}")
优化器必须按顺序执行的三个步骤
- optimizer.zero_grad():梯度归零
- optimizer.zero_grad()函数会遍历模型的所有参数,通过p.grad.detach_()方法截断反向传播的梯度流,再通过p.grad.zero_()函数将每个参数的梯度值设为0,即上一次的梯度记录被清空。
- 因为训练的过程通常使用mini-batch方法,所以如果不将梯度清零的话,梯度会与上一个batch的数据相关,因此该函数要写在反向传播和梯度下降之前。
- 常规情况下,每个batch需要调用一次optimizer.zero_grad()函数,把参数的梯度清零;也可以多个batch只调用一次optimizer.zero_grad()函数,这样相当于增大了batch_size。
- loss.backward():反向传播计算得到每个参数的梯度值
- 如果你设置tensor的requires_grads为True,就会开始跟踪这个tensor上面的所有运算,如果你做完运算后使用tensor.backward(),所有的梯度就会自动运算,tensor的梯度将会累加到它的.grad属性里面去。
- 损失函数loss是由模型的所有权重w经过一系列运算得到的,若某个w的requires_grads为True,则w的所有上层参数(后面层的权重w)的.grad_fn属性中就保存了对应的运算,然后在使用loss.backward()后,会一层层的反向传播计算每个w的梯度值,并保存到该w的.grad属性中。
- optimizer.step():通过梯度下降执行一步参数更新
- step()函数的作用是执行一次优化步骤,通过梯度下降法来更新参数的值
- optimizer只负责通过梯度下降进行优化,而不负责产生梯度,梯度是tensor.backward()方法产生的。
linear_model = nn.Linear(1, 1)
optimizer = optim.SGD(linear_model.parameters(), lr=1e-2)
training_loop(
n_epochs = 3000,
optimizer = optimizer,
model = linear_model,
loss_fn = nn.MSELoss(), # 即均方误差函数
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = t_c_train,
t_c_val = t_c_val)
print()
print(linear_model.weight)
print(linear_model.bias)
3. 完成一个神经网络
3.1. 替换线性模型
构建一个最简单的神经网络:一个线性模块,然后是一个激活函数,输入到另一个线性模块
第一个线性模型+激活层通常被称为隐藏层,因为它的输出并不是直接能够观察到的。而是被输入到下一层。
nn提供了一种通过nn.Sequential容器来连接模型的方式
seq_model = nn.Sequential(
nn.Linear(1, 13), # 我们随便指定输出张量的大小为13,我们是想该张量的大小与其他张量的形状大小不一样
nn.Tanh(),
nn.Linear(13, 1)) # 这里的张量形状大小值13必须与前一个模块输出张量的大小相等
seq_model
3.2. 检查参数
[param.shape for param in seq_model.parameters()]
通过名称识别参数
for name, param in seq_model.named_parameters():
print(name, param.shape)
使用OrderedDict确保层的顺序,并用它来命名传递给Sequential的每个模块
from collections import OrderedDict
seq_model = nn.Sequential(OrderedDict([
('hidden_linear', nn.Linear(1, 8)),
('hidden_activation', nn.Tanh()),
('output_linear', nn.Linear(8, 1))
]))
seq_model
为子模块获取更多解释性名词
for name, param in seq_model.named_parameters():
print(name, param.shape)
访问特定参数
seq_model.output_linear.bias
进行一次训练循环,输出最后一个迭代周期之后的梯度结果
optimizer = optim.SGD(seq_model.parameters(), lr=1e-3) # 为了提高稳定性,我们降低了学习率
training_loop(
n_epochs = 5000,
optimizer = optimizer,
model = seq_model,
loss_fn = nn.MSELoss(),
t_u_train = t_un_train,
t_u_val = t_un_val,
t_c_train = t_c_train,
t_c_val = t_c_val)
print('output', seq_model(t_un_val))
print('answer', t_c_val)
print('hidden', seq_model.hidden_linear.weight.grad)
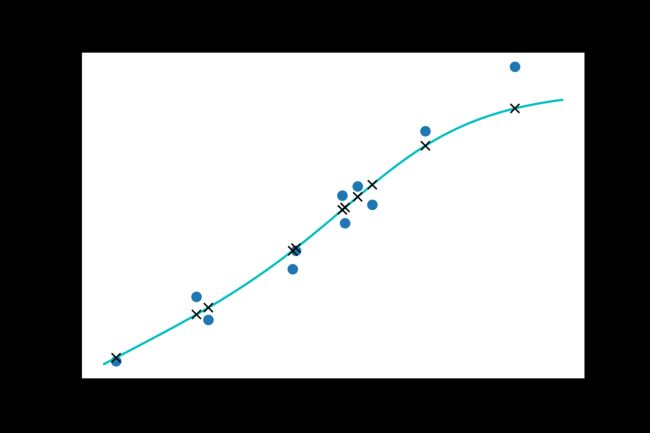
3.2. 与线性模型对比
from matplotlib import pyplot as plt
t_range = torch.arange(20., 90.).unsqueeze(1)
fig = plt.figure(dpi=600)
plt.xlabel("Fahrenheit")
plt.ylabel("Celsius")
plt.plot(t_u.numpy(), t_c.numpy(), 'o')
plt.plot(t_range.numpy(), seq_model(0.1 * t_range).detach().numpy(), 'c-')
plt.plot(t_u.numpy(), seq_model(0.1 * t_u).detach().numpy(), 'kx')
总结
本文主要讲解了:
- 神经网络与线性模型相比,非线性激活函数是主要的差异
- 使用PyTorch的nn模块
- 用神经网络求解线性拟合问题