pytorch实现吴恩达机器学习课后作业——线性回归
线性回归
题目和数据
-
题目:使用ex1data1.txt中给出的两个变量,分别设为x,y,来预测卡车利润(y)的收益值。
在数据集,第一列表示城市人数(x),第二列该城市的卡车利润(y) -
数据集:
6.1101,17.592
5.5277,9.1302
8.5186,13.662
7.0032,11.854
5.8598,6.8233
8.3829,11.886
7.4764,4.3483
8.5781,12
6.4862,6.5987
5.0546,3.8166
5.7107,3.2522
14.164,15.505
5.734,3.1551
8.4084,7.2258
5.6407,0.71618
5.3794,3.5129
6.3654,5.3048
5.1301,0.56077
6.4296,3.6518
7.0708,5.3893
6.1891,3.1386
20.27,21.767
5.4901,4.263
6.3261,5.1875
5.5649,3.0825
18.945,22.638
12.828,13.501
10.957,7.0467
13.176,14.692
22.203,24.147
5.2524,-1.22
6.5894,5.9966
9.2482,12.134
5.8918,1.8495
8.2111,6.5426
7.9334,4.5623
8.0959,4.1164
5.6063,3.3928
12.836,10.117
6.3534,5.4974
5.4069,0.55657
6.8825,3.9115
11.708,5.3854
5.7737,2.4406
7.8247,6.7318
7.0931,1.0463
5.0702,5.1337
5.8014,1.844
11.7,8.0043
5.5416,1.0179
7.5402,6.7504
5.3077,1.8396
7.4239,4.2885
7.6031,4.9981
6.3328,1.4233
6.3589,-1.4211
6.2742,2.4756
5.6397,4.6042
9.3102,3.9624
9.4536,5.4141
8.8254,5.1694
5.1793,-0.74279
21.279,17.929
14.908,12.054
18.959,17.054
7.2182,4.8852
8.2951,5.7442
10.236,7.7754
5.4994,1.0173
20.341,20.992
10.136,6.6799
7.3345,4.0259
6.0062,1.2784
7.2259,3.3411
5.0269,-2.6807
6.5479,0.29678
7.5386,3.8845
5.0365,5.7014
10.274,6.7526
5.1077,2.0576
5.7292,0.47953
5.1884,0.20421
6.3557,0.67861
9.7687,7.5435
6.5159,5.3436
8.5172,4.2415
9.1802,6.7981
6.002,0.92695
5.5204,0.152
5.0594,2.8214
5.7077,1.8451
7.6366,4.2959
5.8707,7.2029
5.3054,1.9869
8.2934,0.14454
13.394,9.0551
5.4369,0.61705
pytorch实现流程
导入包
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable
import torch.nn as nn
得到并处理数据
#得到数据
data = np.loadtxt('ex1data2.txt',delimiter=',')
x = data[:,0]
y = data[:,1]
# plt.scatter(x,y)
# plt.show()
#处理数据
x = np.array(x,dtype='float32')
x = x.reshape(-1,1)
x = Variable(torch.from_numpy(x))
y = np.array(y,dtype='float32')
y = y.reshape(-1,1)
y = Variable(torch.from_numpy(y))
必须要将得到的数据转成torch矩阵形式。
训练模型并传入维度
class LinearRegression(nn.Module):
def __init__(self,input_size,output_size):
super(LinearRegression,self).__init__()
self.linear = nn.Linear(input_dim,output_dim)
def forward(self,the):
return self.linear(the)
#定义模型
input_dim = 1
output_dim = 1
model = LinearRegression(input_dim,output_dim)
LinearRegression线性回归函数是自定义的,而nn.Linear是官方给出的函数,所以传入input_dim,output_dim两个维度(即输入和输出各是多少变量)。并在其中做好前向传播。

model是得到线性回归这一模型,方便之后运用。
设置损失函数和优化函数,找到最合适的学习率
#MSE损失函数
mse = nn.MSELoss()
#找最合适的学习率α,使得误差最小
learning_rate = 1e-2 #决定能够多快到达最低点
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate) #优化函数
损失函数nn.MSELoss()是为了找到误差。

优化函数torch.optim.SGD(),对模型进行优化,相当于梯度下降的作用。
其中的lr储存学习率α。

训练模型,降低损失
#训练模型,降低损失
# loss_list = []
iteration_number = 1001 #迭代次数
for iteration in range(iteration_number):
#向前传播计算损失函数
results = model(x) #训练模型,向前得到结果
loss = mse(results,y) #损失函数
#向后传播计算梯度
optimizer.zero_grad() #优化器.参数梯度置零,每次迭代都要清零
loss.backward() #反向传播
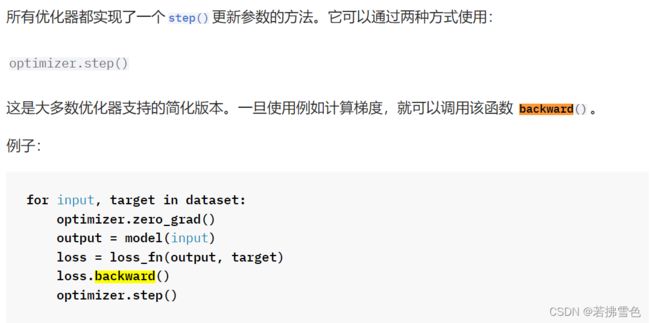
optimizer.step() #更新参数
# loss_list.append(loss.data) #储存损失
if (iteration % 50 == 0):
print('epoch {},loss {}'.format(iteration,loss.data))
规定迭代次数,多次传参,提高精准度。
model是线性回归函数,其中自带前向传播得到处理后的数据。再调用损失函数mse()计算得到误差值(损失)。
optimizer.zero_grad()将在每次迭代过程中将梯度重新置零,以便计算梯度。

loss.backward()是将得到的损失函数反向传播,计算梯度,并使用optimizer.step()更新参数。
进行预测,数据可视化
#进行预测
predicted = model(x).data.numpy()
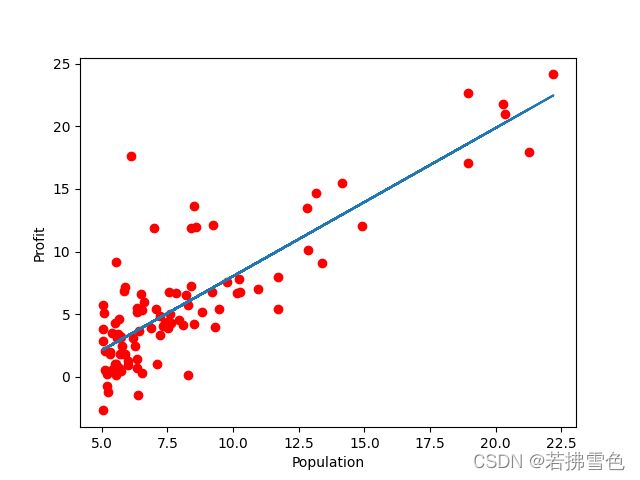
plt.plot(x, y, 'ro', label='Original Data')
plt.plot(x, predicted, label='Fitting Line')
#数据可视化
plt.xlabel("Population")
plt.ylabel("Profit")
plt.show()
predicted得到处理后的拟合数据。
并使用plt进行作图,实现数据可视化。
最后结果
完整代码
import numpy as np
import matplotlib.pyplot as plt
import torch
from torch.autograd import Variable
import torch.nn as nn
# import warnings
# warnings.filterwarnings("ignore")
#得到数据
data = np.loadtxt('ex1data1.txt',delimiter=',')
x = data[:,0]
y = data[:,1]
# plt.scatter(x,y)
# plt.show()
#处理数据
x = np.array(x,dtype='float32')
x = x.reshape(-1,1)
x = Variable(torch.from_numpy(x))
y = np.array(y,dtype='float32')
y = y.reshape(-1,1)
y = Variable(torch.from_numpy(y))
print(x)
#训练模型
class LinearRegression(nn.Module):
def __init__(self,input_size,output_size):
super(LinearRegression,self).__init__()
self.linear = nn.Linear(input_dim,output_dim)
def forward(self,the):
return self.linear(the)
#定义模型
input_dim = 1
output_dim = 1
model = LinearRegression(input_dim,output_dim)
#MSE损失函数
mse = nn.MSELoss()
#找最合适的学习率α,使得误差最小
learning_rate = 1e-2 #决定能够多块到达最低点
optimizer = torch.optim.SGD(model.parameters(),lr=learning_rate) #优化函数
#训练模型,降低损失
# loss_list = []
iteration_number = 1001 #迭代次数
for iteration in range(iteration_number):
#向前传播计算损失函数
results = model(x) #训练模型,向前得到结果
loss = mse(results,y) #损失函数
#向后传播计算梯度
optimizer.zero_grad() #优化器.参数梯度置零,每次迭代都要清零
loss.backward() #反向传播
optimizer.step() #更新参数
# loss_list.append(loss.data) #储存损失
if (iteration % 50 == 0):
print('epoch {},loss {}'.format(iteration,loss.data))
#进行预测
predicted = model(x).data.numpy()
plt.plot(x, y, 'ro', label='Original Data')
plt.plot(x, predicted, label='Fitting Line')
#数据可视化
plt.xlabel("Population")
plt.ylabel("Profit")
plt.show()
print("训练结束")