操作符知识你会了，那表达式求值呢？

大家好呀！我是小杨。小杨前面将C语言中的操作符这部分知识做了一个大总结，想必大家认真看后应该收获颇多吧。那么今天就对表达式求值这部分内容进行归纳一下，在方便自己复习的同时也能够帮助到大家。加油，追梦人！

---

文章目录

✍表达式求值

✍1，隐式类型转换

✍2，算术转换

✍3，操作符属性

---

✍表达式求值

表达式求值的顺序一部分是由操作符的优先级和结合性决定。

同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型。

---

✍1，隐式类型转换

C的整型算术运算总是至少以缺省整型类型的精度来进行的。

为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

整型提升的意义：
表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度
一般就是int的字节长度，同时也是CPU的通用寄存器的长度。

因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长
度。

通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令
中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转
换为int或unsigned int，然后才能送入CPU去执行运算。

---

为了能够更好的理解其用法，小杨通过几个实例来进行讲解。

实例：

#include
int main()
{
	char a = 5;
	char b = -13;
	char c = a + b;
	printf("%d", c);
	return 0;
}

CPU执行运算流程：
a和b的值被提升为普通整型，然后再执行加法运算。
加法运算完成之后，结果将被截断，然后再存储于c中。

扩展：截断是把大类型的数据给小空间类型的数据赋值的时候，因为小类型空间不足，所以产生截断。

在这里，小杨先给大家扩展一个小知识：如何进行整体提升呢？
解答：整形提升是按照变量的数据类型的符号位来提升的。

为了能够更好的理解整型提升是如何进行的，小杨举了下述整形提升的例子。

负数的整形提升
char c1 = -1;
变量c1的二进制位(补码)中只有8个比特位：
1111111
因为 char 为有符号的 char，
所以整形提升的时候，高位补充符号位，即为1
提升之后的结果是：
11111111111111111111111111111111

正数的整形提升
char c2 = 1;
变量c2的二进制位(补码)中只有8个比特位：
00000001
因为 char 为有符号的 char
所以整形提升的时候，高位补充符号位，即为0
提升之后的结果是：
00000000000000000000000000000001

切记：无符号整形提升，高位补0

知道了如何将char类型和short短整型类是如何进行整型提升的，那么回到之前最先那个实例，这个实例的程序输出结果是什么，大家应该都知道如何去运算也能求出正确的答案了吧。

通过打印输出实例结果：

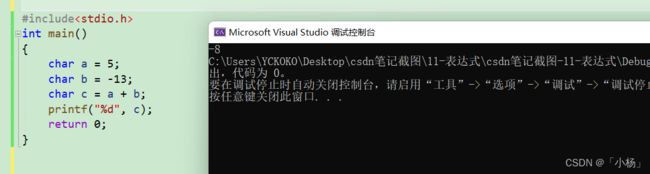
分析流程：

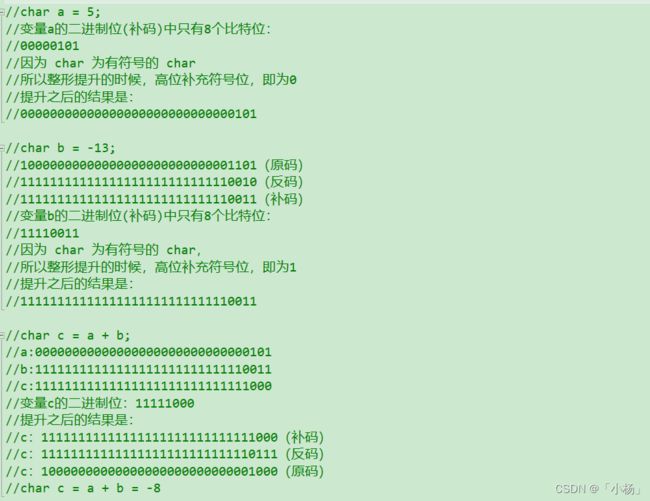
通过上述流程得到的结果与程序代码打印出的结果相同，我们可以知道流程没有出错。

---

到这里，可能还有一些小伙伴还是对整型转换这个知识点不太理解，别急，小杨再举个实例。

实例2：

#include
int main()
{
	char a = 0xb6;
	short b = 0xb600;
	int c = 0xb6000000;
	if (a == 0xb6)
		printf("a");
	if (b == 0xb600)
		printf("b");
	if (c == 0xb6000000)
		printf("c");
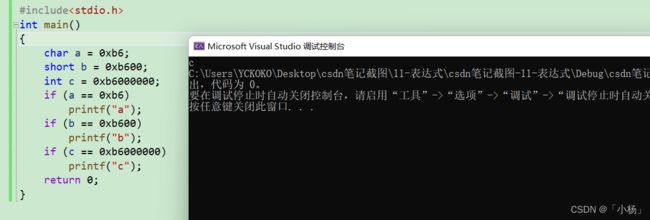
	return 0;
}

小伙伴们，能够知道这个实例的输出结果吗？如果可以，说明你已经掌握了整型提升这个知识点；如果不可以也不要灰心，对这个知识点多看几遍就行，俗话说：孰能生巧，没有什么是一蹴而就的。

说明：其实这个实例不会很难，实例中的a,b要进行整形提升,但是c不需要整形提升，a,b整形提升之后,变成了负数,所以表达式 a==0xb6 , b==0xb600 的结果为假,但是c不发生整形提升,则表达式c==0xb6000000 的结果是真，所程序输出的结果是c。

实例输出结果：

---

由此返回目录

✍2，算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类
型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

long double 多精度浮点类型或长精度浮点类型
double 双精度浮点型
float 单精度浮点型
unsigned long int 无符号长整型
long int 长整型
unsigned int 无符号整型
int 整型

如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。

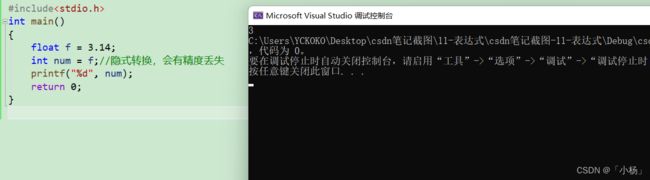
如果double双精度浮点型的数与int整型的数进行运算，要先把int型数据提升转换为double型数据，然后再执行相应的运算，运算完成之后，结果将被截断，然后再存储于c中。

#include
int main()
{
	double a = 5.0;
	int b = -13;
	int c = a + b;
	printf("%d", c);
	return 0;
}

实例输出结果：

警告:算术转换要合理，否则会出现一些潜在的风险。

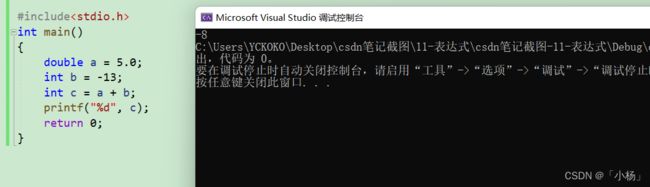
实例：

#include
int main()
{
	float f = 3.14;
	int num = f;//隐式转换，会有精度丢失
	printf("%d", num);
	return 0;
}

实例输出结果：

最后，小杨在系统归纳一下算术转换：

算术转换，是两个不同类型数据运算的时候需要解释为相同类型进行计算。

比如有符号和无符号，会把有符号的数据当做无符号参与运算，-1会被解释成为很大的一个数字， 还有整形和浮点型会解释成为浮点型之后参与运算。

换而言之，我们也可以这样理解，算术转换就是编译器做的特殊处理而已，知道有符号和无符号运算转成无符号参与，整形与浮点，会转成浮点参与运算就行。

具体情况具体分析，空说其实没有太大意义，先了解这些功能就行。

---

由此返回目录

✍3，操作符属性

复杂表达式的求值有三个影响的因素。
1. 操作符的优先级
2. 操作符的结合性
3. 是否控制求值顺序。

两个相邻的操作符先执行哪个？
取决于他们的优先级。如果两者的优先级相同，取决于他们的结合性。

各操作符的相关性质如下表所示：

操作符	描述	用法示例	结果类型	结合性	是否控制求值顺序
（)	聚组	（表达式）	与表达式同	N/A	否
（）	函数调用	rexp（rexp，…,rexp）	rexp	L-R	否
[ ]	下标引用	rexp[rexp]	lexp	L-R	否
.	访问结构成员	lexp.member_name	lexp	L-R	否
->	访问结构指针成员	rexp->member_name	lexp	L-R	否
++	后缀自增	lexp ++	rexp	L-R	否
–	后缀自减	lexp –	rexp	L-R	否
!	逻辑反	! rexp	rexp	R-L	否
~	按位取反	~ rexp	rexp	R-L	否
+	单目，表示正值	+ rexp	rexp	R-L	否
-	单目，表示负值	- rexp	rexp	R-L	否
++	前缀自增	++ lexp	rexp	R-L	否
–	前缀自减	– lexp	rexp	R-L	否
*	间接访问	* rexp	lexp	R-L	否
&	取地址	& lexp	rexp	R-L	否
sizeof	取其长度，以字节表示sizeof rexp	sizeof(类型)	rexp	R-L	否
(类型）	类型转换	(类型) rexp	rexp	R-L	否
*	乘法	rexp * rexp	rexp	L-R	否
/	除法	rexp / rexp	rexp	L-R	否
%	整数取余	rexp %	rexp	L-R	否
+	加法	rexp + rexp	rexp	L-R	否
-	减法	rexp - rexp	rexp	L-R	否
<<	左移位	rexp << rexp	rexp	L-R	否
>>	右移位	rexp >> rexp	rexp	L-R	否
>	大于	rexp > rexp	rexp	L-R	否
>=	大于等于	rexp >= rexp	rexp	L-R	否
<	小于	rexp < rexp	rexp	L-R	否
<=	小于等于	rexp <= rexp	rexp	L-R	否
==	等于	rexp == rexp	rexp	L-R	否
!=	不等于	rexp != rexp	rexp	L-R	否
&	位与	rexp & rexp	rexp	L-R	否
^	位异或	rexp ^ rexp	rexp	L-R	否
|	位或	rexp| rexp	rexp	L-R	否
&&	逻辑与	rexp && rexp	rexp	L-R	是
||	逻辑或	rexp || rexp	rexp	L-R	是
? :	条件操作符	rexp ? rexp : rexp	rexp	N/A	是
=	赋值	lexp = rexp	rexp	R-L	否
+=	以…加	lexp += rexp	rexp	R-L	否
-=	以…减	lexp -= rexp	rexp	R-L	否
*=	以…乘	lexp *= rexp	rexp	R-L	否
/=	以…除	lexp /= rexp	rexp	R-L	否
%=	以…取模	lexp %= rexp	rexp	R-L	否
<<=	以…左移	lexp <<= rexp	rexp	R-L	否
>>=	以…右移	lexp >>= rexp	rexp	R-L	否
&=	以…与	&= rexp	rexp	R-L	否
^=	以…异或	lexp ^= rexp	rexp	R-L	否
|=	以…或	lexp | = rexp	rexp	R-L	否
，	逗号	rexp，rexp	rexp	L-R	是

操作符优先级：由上到下依次降低。

小杨在这里提醒一下：这个详细记录各操作符的性质的表不需要刻意地去被背诵，只需要掌握一些常见的操作符用法就可以了，了解个大概即可。

---

由此返回目录

结语

小伙伴们，当你学到这里的时候，你们应该对表达式求值部分的内容已经有了全新的认识吧！后续小杨会给大家总结其他的内容，不断更新优质的内容来帮助大家，一起进步。加油，追梦人!让我们一起拥抱美好明天!

---