全面了解操作符的表达式求值

作者介绍：友友们好我是沐曦希，可以叫我小沐
作者主页：沐曦希的个人博客主页.
作者的gitee：https://gitee.com/muxi-c-language.
零基础学习C语言系列：
https://blog.csdn.net/m0_68931081/category_11742786.html.
小沐和友友们一样喜欢编辑，天天敲代码，沉迷学习，日渐消瘦。很荣幸能向大家分享我的所学，和大家一起进步，成为合格的卷王。✨如果文章有错误，欢迎在评论区✏️指正。那么开始今天的学习吧！

表达式求值

在计算操作符的表达式求值时，经常需要考虑的是表达式求值的顺序和类型转换。
例如：

#include
int main()
{
	char a = 3;
	int b = 5;
	int c = a++ + b;//此时a进行了类型转换，由char类型转换成int类型，由8个比特位变成32个比特位，后置++的优先级大于+，后置++是先使用，后++。
	int d = ++a + b;//此时a进行了类型转换。
	printf("a=%d,b=%d,c=%d,d=%d", a, b, c, d);
	return 0;
}

表达式求值的顺序一部分是由操作符的优先级和结合性决定。
同样，有些表达式的操作数在求值的过程中可能需要转换为其他类型。

隐式类型转换

C的整型算术运算总是至少以缺省（默认）整型类型的精度来进行的。
为了获得这个精度，表达式中的字符和短整型操作数在使用之前被转换为普通整型，这种转换称为整型提升。

整型提升的意义：

表达式的整型运算要在CPU的相应运算器件内执行，CPU内整型运算器(ALU)的操作数的字节长度一般就是int的字节长度，同时也是CPU的通用寄存器的长度。
因此，即使两个char类型的相加，在CPU执行时实际上也要先转换为CPU内整型操作数的标准长度。
通用CPU（general-purpose CPU）是难以直接实现两个8比特字节直接相加运算（虽然机器指令中可能有这种字节相加指令）。所以，表达式中各种长度可能小于int长度的整型值，都必须先转换为int或unsigned int，然后才能送入CPU去执行运算。

例如：

#include
int main()
{
	char a = 5;
	char b = 126;
	char c = a + b;
	printf("%d\n", c);
	return 0;
}

//实例1
char a,b,c;
...
a = b + c;

b和c的值被提升为普通整型，然后再执行加法运算。
加法运算完成之后，结果将被截断，然后再存储于a中。
那么如何进行整型提升呢：

整形提升是按照变量的数据类型的符号位来提升的

//负数的整形提升：
char c1 = -1;
//变量c1的二进制位(补码)中只有8个比特位（bit)：1111111
//因为 char 为有符号的 char
//所以整形提升的时候，高位补充符号位，即为1
///提升之后的结果是：11111111111111111111111111111111

//正数的整形提升：
char c2 = 1;
//变量c2的二进制位(补码)中只有8个比特位(bit)：00000001
//因为 char 为有符号的 char
//所以整形提升的时候，高位补充符号位，即为0
//提升之后的结果是：00000000000000000000000000000001
//无符号整形提升，高位补0

整形提升的例子:

//实例1
#include
int main()
{
	char a = 0xb6;
	short b = 0xb600;
	int c = 0xb6000000;
	if (a == 0xb6)
		printf("a");
	if (b == 0xb600)
		printf("b");
	if (c == 0xb6000000)
		printf("c");
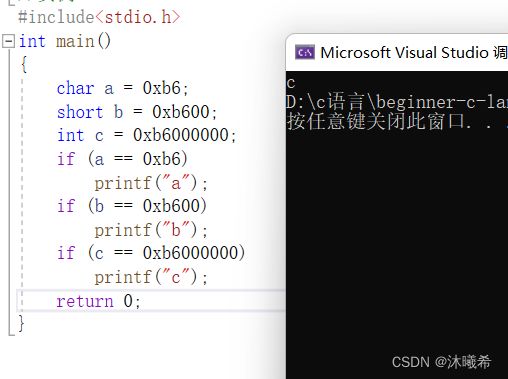
	return 0;
}

实例1中的a,b要进行整形提升,但是c不需要整形提升
a,b整形提升之后,变成了负数,所以表达式1，2的结果是假,但是c不发生整形提升,则表达式c==0xb6000000 的结果是真.

//实例2
#include
int main()
{
	char c = 1;
	printf("%zu\n", sizeof(c));
	printf("%zu\n", sizeof(+c));
	printf("%zu\n", sizeof(-c));
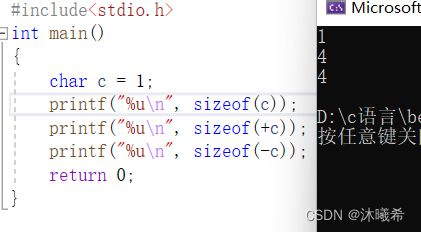
	return 0;
}

c只要参与表达式运算,就会发生整形提升,表达式+c ,就会发生提升,所以sizeof(+c) 是4个字节.
表达式-c 也会发生整形提升,所以sizeof(-c) 是4个字节,但是sizeof© ,就是1个字节.

算术转换

如果某个操作符的各个操作数属于不同的类型，那么除非其中一个操作数的转换为另一个操作数的类型，否则操作就无法进行。下面的层次体系称为寻常算术转换。

long double//多精度浮点类型或长精度浮点类型
double//双精度浮点数
float//单精度浮点数
unsigned long int//无符号长整型
long int//长整型
unsigned int//无符号整型
int//整型

如果某个操作数的类型在上面这个列表中排名较低，那么首先要转换为另外一个操作数的类型后执行运算。

在合理转换的过程中也会出现一些问题：

#include
int main()
{
	float f = 3.14;
	int num = f;//隐式转换，会有精度丢失
	printf("%d", num);
	return 0;
}

操作符的属性

在进行复杂的表达式计算时候，往往需要考虑以下三种因素：

1. 操作符的优先级
2. 操作符的结合性
3. 是否控制求值顺序。

相邻的两个操作符，先进行哪个运算，取决与他们的优先级，如果优先级相同则取决于结合性，操作符的优先级。
操作符优先级：

操作符	描述	用法实例	结果类型	结合性	是否控制求和顺序
（）	聚组	（表达式）	与表达式同	N/A	否
（）	函数调用	rexp（rexp，…,rexp）	rexp	L-R	否
[ ]	下标引用	rexp[rexp]	lexp	L-R	否
.	访问结构成员	lexp.member_name	lexp	L-R	否
->	访问结构指针成员	rexp->member_name	lexp	L-R	否
++	后缀自增	lexp ++	rexp	L-R	否
--	后缀自减	lexp –	rexp	L-R	否
!	逻辑反	! rexp	rexp	R-L	否
~	按位取反	~ rexp	rexp	R-L	否
+	单目，表示正值	+ rexp	rexp	R-L	否
-	单目，表示负值	- rexp	rexp	R-L	否
++	前缀自增	++ lexp	rexp	R-L	否
--	前缀自减	– lexp	rexp	R-L	否
*	间接访问	* rexp	lexp	R-L	否
&	取地址	& lexp	rexp	R-L	否
sizeof	取其长度，以字节表示	sizeof rexp sizeof(类型)	rexp	R-L	否
(类型）	类型转换	(类型) rexp	rexp	R-L	否
*	乘法	rexp * rexp	rexp	L-R	否
/	除法	rexp / rexp	rexp	L-R	否
%	整数取余	rexp % rexp	rexp	L-R	否
+	加法	rexp + rexp	rexp	L-R	否
-	减法	rexp - rexp	rexp	L-R	否
<<	左移位	rexp << rexp	rexp	L-R	否
>>	右移位	rexp >> rexp	rexp	L-R	否
>	大于	rexp > rexp	rexp	L-R	否
>=	大于等于	rexp >= rexp	rexp	L-R	否
<	小于	rexp < rexp	rexp	L-R	否
<=	小于等于	rexp <= rexp	rexp	L-R	否
==	等于	rexp == rexp	rexp	L-R	否
!=	不等于	rexp != rexp	rexp	L-R	否
&	位与	rexp & rexp	rexp	L-R	否
^	位异或	rexp ^ rexp	rexp	L-R	否
|	位或	rexp | rexp	rexp	L-R	否
&&	逻辑与	rexp && rexp	rexp	L-R	是
||	逻辑或	rexp || rexp	rexp	L-R	是
? :	条件操作符	rexp ? rexp : rexp	rexp	N/A	是
=	赋值	lexp = rexp	rexp	R-L	否
+=	以…加	lexp += rexp	rexp	R-L	否
-=	以…减	lexp -= rexp	rexp	R-L	否
*=	以…乘	lexp *= rexp	rexp	R-L	否
/=	以…除	lexp /= rexp	rexp	R-L	否
%=	以…取模	lexp %= rexp	rexp	R-L	否
<<=	以…左移	lexp <<= rexp	rexp	R-L	否
>>=	以…右移	lexp >>= rexp	rexp	R-L	否
&=	以…与	lexp &= rexp	rexp	R-L	否
^=	以…异或	lexp ^= rexp	rexp	R-L	否
|=	以…或	lexp	= rexp	rexp	R-L
，	逗号	rexp，rexp	rexp	L-R	是

☠️一些问题表达式:

//表达式的求值部分由操作符的优先级决定。
//表达式1
a*b + c*d + e*f

注释：代码1在计算的时候，由于*比+的优先级高，只能保证，的计算是比+早，但是优先级并不 能决定第三个比第一个+早执行。

所以表达式的计算机顺序就可能是：

a*b
c*d
a*b + c*d
e*f
a*b + c*d + e*f
//或者：
a*b
c*d
e*f
a*b + c*d
a*b + c*d + e*f

//表达式2
c + --c;

注释：同表达式1，操作符的优先级只能决定自减–的运算在+的运算的前面，但是我们并没有办法得知，+操作符的左操作数的获取在右操作数之前还是之后求值，所以结果是不可预测的，是有歧义
的。

//代码3-非法表达式
#include
int main()
{
    int i = 10;
    i = i-- - --i * ( i = -3 ) * i++ + ++i;
    printf("i = %d\n", i);
    return 0;
}

表达式3在不同编译器中测试结果：非法表达式程序的结果。友友们可以在不同的编译器下测试一下。

//代码4
#include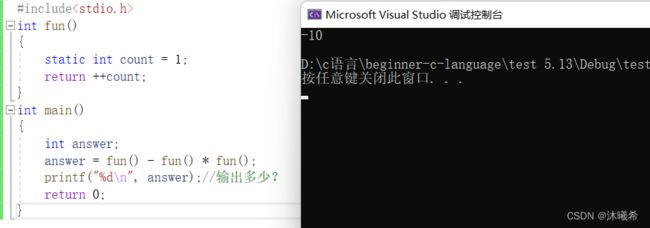
int fun()
{
	static int count = 1;
	return ++count;
}
int main()
{
	int answer;
	answer = fun() - fun() * fun();
	printf("%d\n", answer);//输出多少？
	return 0;
}

这个代码问题：虽然在大多数的编译器上求得结果都是相同的。
但是上述代码answer = fun() - fun() * fun(); 中我们只能通过操作符的优先级得知：先算乘法，再算减法。
函数的调用先后顺序无法通过操作符的优先级确定。

//代码5
#include 
int main()
{
int i = 1;
int ret = (++i) + (++i) + (++i);
printf("%d\n", ret);
printf("%d\n", i);
return 0;
}

上面的代码也是在不同的编译器的环境下值不同。

这段代码中的第一个+ 在执行的时候，第三个++是否执行，这个是不确定的，因为依靠操作符的优先级和结合性是无法决定第一个+ 和第三个前置++
的先后顺序。

总结：我们写出的表达式如果不能通过操作符的属性确定唯一的计算路径，那这个表达式就是存在问题的。

写在最后

那么今天的学习就到这里了。友友们觉得不错的可以给个关注，点赞或者收藏哦！感谢各位友友们的支持。以下的代码希望各位大佬们自行检验哦，毕竟亲手操作让记忆更加深刻。

你的❤️点赞是我创作的动力的源泉
你的✨收藏是我奋斗的方向
你的关注是对我最大的支持
你的✏️评论是我前进的明灯
创作不易，希望大佬你支持一下小沐吧

下一期见了！