ai俄罗斯方块java_俄罗斯方块 AI 算法讲解
俄罗斯方块游戏可以说是一个非常古老的游戏了,而游戏 AI 这个话题也已经被人反复研究多次,特别是最近几年机器学习和深度学习大火特火,二者的结合显然不言而喻。不过在早期,貌似即使最先进的算法也无法超过专业人员在没有时间压力下的水平。
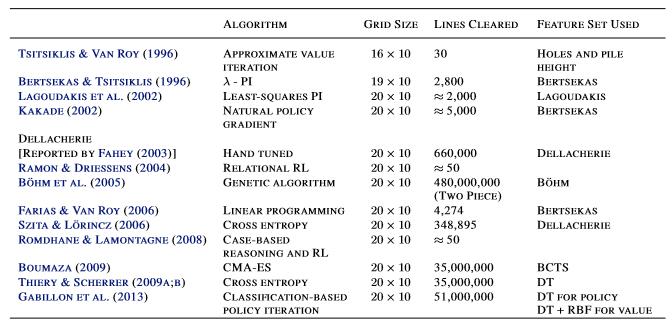
不过目前我随便在网上搜一搜,发现在 2013 年的时候,就有算法可以达到5千万级别的消行量,显然这已经比一般人强得多了,前提是你能玩那么久……
咱们今天不讲复杂的算法,而是讲一种普通 AI 算法的实现过程,该算法是 Pierre Dellacherie 的改进版,被原作者称作 El-Tetris,原始出处如下:El-Tetris – An Improvement on Pierre Dellacherie’s Algorithm。
1. 传统 AI 的逻辑
事实上不要一听到 AI 就感觉很高大上,普通的 AI 算法是非常简单的,就是枚举所有可能发生的场景,根据一些特征对这些场景打分,分数越高(越低)就越好,El-Tetris 就是这套思路。这种传统的 AI 算法关键点在于如何寻找这些特征点,以及如何确定这些特征点的比例系数。
假设俄罗斯方块在游戏的过程中可以抽象出几个特征点,分别用 $x_0、x_1、x_2 … x_n $ 来表示, 而这些特征在游戏中所占的重要比例是不同的,假设它们所占的比例分别是 ${\beta_0}、{\beta_1}、{\beta_2} … {\beta_n}$ 这时候我们可以用多元线性回归的方式将它们组织起来:
$
y = {\beta_0}x_0 + {\beta_1}x_1 + {\beta_2}x_2 + {\beta_3}x_3 … {\beta_n}x_n
$
这里有一点需要说明,这些 $ x $ 变量之间应该是相互独立的,相关性不能太强。举个例子,假设 $ x_0 $ 代表方块落下后的容器高度,$ x_1 $ 代表方块落下后距离容器上方的高度,这两个变量就可以看作强相关,因为你可以通过它们中的任何一个推算出另一个,也就是说二者其实在式子中是可以合并的,既然可以合并,显然没有必要用两个变量来表示这个特征。
在这个式子中,我们可以用向量 $X$ 表示所有的特征点,即 $(x_0,x_1,x_2, …, x_n)$,这些特征点是可以根据当前方块的状态推导出来,可以算作已知条件。对应的向量 $({\beta_0}, {\beta_1}, {\beta_2} … {\beta_n})$ 也可以用 ${\beta}$ 表示,这个 ${\beta}$ 是一个经验值,是使用数学方法或者机器学习方法等手段推算出的经验值,这个值也是已知的。所以最后,我们总是可以通过向量 $X$ 和向量 ${\beta}$ 算出最后的结果 $y$,总结即:
$
y = {\beta}X
$
2. El-Tetris 算法的特征
看过上面的公式,你可能仍然一脸懵逼,但是没关系,理论说起来复杂的一逼,但是实战起来,你就会发现简单的难以置信,先让我们看一看上面的向量 $X$ 是如何计算的。在 El-Tetris 算法中,向量 $X$ 是一个六维向量,每个分量代表一个特征点,下面我们就分别介绍一下它们的具体含义。
首先第一个特征点是 Landing Height。表示当前方块放置之后的高度。这个高度的计算方法是使用当前容器内方块的高度加上当前下落方块的一半。
第二个特征点是 Rows eliminated。表示当前方块落下后被消减的行数。
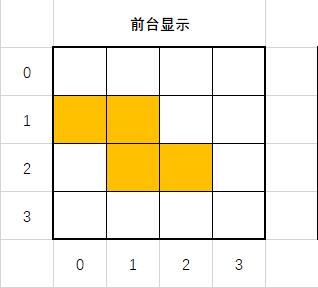
第三个特征点是 Row Transitions。代表容器中水平方向上变换的次数。举个例子:
看图上的最后一行左边数第三列是个洞,所以第二列到第三列这种从有方块到无方块的变化算作一次行变换。对应的第三列到第四列从无方块到有方块也算作一次行变化,所以最后一行的行变换可以算作 2。而我们最终要求的是所有行的变化次数,从上到下一次可得:
2 + 4 + 2 + 2 + 2 + 2 + 2
最后在上图中的情况,第三个特征点最后求得的值是 16。这里注意从上到下第一行是 2 的原因在于,默认情况下,图的左边越界的部分和图的右边越界的部分算作有方块的情况,所以第一行是从有到无到有,所以记作 2 。
第四个特征点是 Column Transitions。和第三个特征点类似,只不过这一次算的是列变换而已。
第五个特征点是 Number of Holes。代表图中空洞的个数。如下图所示,空洞的个数是 6 。
第六个特征点是 Well Sums。表示 “井” 深的连加和。一个 “井” 代表左右都有方块,而中间为空洞的形状,例如下图中可以看作两个 “井”:
其中左边的 “井” 深为 2,右边的 “井” 深为 1。所以最后的结果:
(1 + 2) + 1
等于 4。
3. El-Tetris 算法的权重
知道如何计算特征向量 $ X $ 之后,我们需要知道如何获得向量 $ {\beta} $ 。前面我们说到向量 ${\beta} $ 表示特征值的重要比例,这个比例一般被称为权重,说白了就是有多重要,具体指的就是这些分量对应的特征分量的重要程度。
在原文中,这些参数是作者通过粒子群优化算法计算出来的,这些值最后都是常量:
FEATURE
WEIGHT
Landing Height
-4.500158825082766
Rows eliminated
3.4181268101392694
Row Transitions
-3.2178882868487753
Column Transitions
-9.348695305445199
Number of Holes
-7.899265427351652
Well Sums
-3.3855972247263626
我们这里直接使用即可。通过前面的公式,输入 $X$ 、${\beta}$ 就可以求出当前状态下的一个综合得分,在 El-Tetris 中得到的分数越大,代表方块下落的位置越好。
4. 提取大方块属性
我们在研究 EI-Tetris 算法的时候,已经知道了这个算法的核心就是 6 种特征的计算,而接下来讲解的就是如何使用代码实时的计算这 6 种特征值的过程。
在计算之前,我们需要将俄罗斯方块中 7 种大方块的属性重新计算,在原有的代码中,我们使用了打表法的形式记录了 7 种大方块的形状,不过这些数据在实现 AI 算法的过程是不够的,我们需要更多:
// AI 需要的初始化方块结构
typedef struct AIBlock
{
unsigned short shape;//原始数字代表形状
int leftSpare;//左侧孔隙
int rightSpare;//右侧孔隙
int topSpare;//上方孔隙
int bottomSpare;//下方孔隙
int width;//宽
int height;//高
} AIBlock;
上面是新的 7 种方块的结构, shape 变量是原有大方块形状所代表的变量:
static unsigned short gBlockList[BT_NUM][BS_NUM] = {
{0x00C6, 0x04C8, 0x00C6, 0x04C8}, //S
{0x006C, 0x08C4, 0x006C, 0x08C4}, //Z
{0x00E8, 0x088C, 0x002E, 0x0C44}, //J
{0x00E2, 0x044C, 0x008E, 0x0C88}, //L
{0x000F, 0x8888, 0x000F, 0x8888}, //I
{0x04C4, 0x00E4, 0x08C8, 0x004E}, //T
{0x00CC, 0x00CC, 0x00CC, 0x00CC} //O
};
现在除了需要大方块表示形状的原始变量,还需要知道这些方块真正的长宽,因为在原来俄罗斯方块的实现过程中,每个大方块相当于用 4 * 4 的矩形表示:
但这有个问题,我们无法获取大方块的真实横纵坐标。就如上图所示,这个方块真实的宽高是 3 * 2 ,其中第 0 行和第 3 行是空行,而第 3 列同样是空列,这些属性在原有的程序中无法直接获取。当然如果你要可以忍受效率的影响,每一次动态计算是可行的。不过为了提高效率,这里我们用这个新的结构重新表示一下现有的方块形状。
之所以要获取这些信息,是为了定位我们大方块的真正位置,看看下面几个示意图:
在原来的代码中,我们这样定义一个大方块:
// 方块
typedef struct Block
{
int row;// 方块水平位置
int col;// 方块垂直位置
BlockType type;// 方块类型
BlockState state;// 方块状态
} Block;
这种表示在原有的游戏中是可行的,但是如果用这个结构表示上方图中的四种大方块,会发现它们的 row 和 col 完全一样,我们无法区分当前大方块是具体的哪一种,为了解决这个问题,所以我们重新定义了大方块的结构描述,说白了就是确定一下大方块周围缝隙的大小。
我们无需重新修改原来的代码,只需要在程序初始化的时候动态的计算一下现有所有大方块这些属性的值就好了,当然你也可以修改原来的结构,不过那样初始化的过程可能稍微麻烦一点。
// 初始化 AI 列表
void initAIBlockList(AIBlock block[][BS_NUM])
{
if (!block) {
return;
}
for (int i = 0; i < BT_NUM; i++)
{
for (int j = 0; j < BS_NUM; j++)
{
unsigned short blockFlag = gBlockList[i][j];
//计算左右两侧空余空间的大小
int leftSpare = 0;
for (int i = 0; i < BLOCK_WIDTH; i++) {
//从左侧开始查
if (!((0x1111 << i) & blockFlag)) {
leftSpare++;
}
else {
break;
}
}
int rightSpare = 0;
for (int i = 0; i < BLOCK_WIDTH; i++) { //从右侧开始查 if (!((0x8888 >> i)& blockFlag)) {
rightSpare++;
}
else {
break;
}
}
//计算上下两侧空余空间的大小
int topSpare = 0;
for (int i = 0; i < BLOCK_HEIGHT; i++) {
//从上侧开始查
if (!((0x000F << (4 * i)) & blockFlag)) {
topSpare++;
}
else {
break;
}
}
int bottomSpare = 0;
for (int i = 0; i < BLOCK_HEIGHT; i++) { //从下侧开始查 if (!((0xF000 >> (4 * i))& blockFlag)) {
bottomSpare++;
}
else {
break;
}
}
//初始化
block[i][j].shape = blockFlag;
block[i][j].leftSpare = leftSpare;
block[i][j].rightSpare = rightSpare;
block[i][j].topSpare = topSpare;
block[i][j].bottomSpare = bottomSpare;
block[i][j].width = BLOCK_WIDTH - leftSpare - rightSpare;
block[i][j].height = BLOCK_HEIGHT - topSpare - bottomSpare;
}
}
}
在原有的方块形状数组之上,我们重新生成了一个数组,并根据原有大方块的表示,计算出这些大方块周围的缝隙,以及大方块真正的宽和高,在接下来的代码中,直接使用新生成的 block 数组即可。
5. 计算 Landing Height
计算 Landing Height 只需要将现有容器的高度加上现有大方块高的一半,代码如下:
//计算 Landing Height
static float getLandingHeight(const Tetris* tetris, BlockType type, BlockState state, int column)
{
const AIBlock* props = getBlockProps(type, state);
assert(props);
//水平越界,给一个无限大的值
if (column > TETRIS_CONTAINER_WIDTH - 2 - props->width) {
return -1.0f;
}
//模拟下落,最终小块的位置
Block block = { 0, -props->leftSpare + column + 1, type, state };
while (!hitTest(&block, tetris)) {
moveDown(&block);
}
block.row -= 1;
float lh = (TETRIS_CONTAINER_HEIGHT - 1) - block.row - props->topSpare - props->height * 0.5f;
assert(lh >= 0);
return lh;
}
函数中 column 表示大方块所在的列,这个列是真正的列,不是原有结构中的 col 属性。我们需要通过 column 的值反向求出当前大方块的位置,即计算出大方块的 row 和 col,接着根据当前大方块的位置模拟真实下落后的状态,最后求出 Landing Height 的特征值。
6. 计算 Rows eliminated
//计算 Rows eliminated
static int getEliminatedRows(const Tetris* tetris, BlockType type, BlockState state, int column)
{
//合并
unsigned long container[TETRIS_CONTAINER_HEIGHT] = { 0 };
int row = getMergedContainer(tetris, type, state, column, container);
if (row < 0) {
return -1;
}
//查看销行
int eraseLine = 0;
for (int i = 0; i < BLOCK_HEIGHT; i++)
{
if (container[row + i] == 0x0FFF) {
eraseLine++;
}
}
return eraseLine;
}
计算消行的内容和原来类似,枚举容器中的行,当出现 0x0FFF 的行时,消行数加 1。
7. 计算 Row Transitions 和 Column Transitions
这两个特征值的计算方法类似,这里只讲解一下 Row Transitions 的计算方块。
//计算 Row Transitions
static getRowTransitions(const Tetris* tetris, BlockType type, BlockState state, int column)
{
//合并
unsigned long container[TETRIS_CONTAINER_HEIGHT] = { 0 };
if (getMergedContainer(tetris, type, state, column, container) < 0) {
return -1;
}
//检测行反转
int transitions = 0;
for (int i = BLOCK_HEIGHT; i < TETRIS_CONTAINER_HEIGHT - 1; i++)
{
int lastBit = 0x01;
for (int j = 0; j < TETRIS_CONTAINER_WIDTH; j++) { unsigned char currBit = (container[i] >> j) & 0x01;
if (currBit != lastBit) {
++transitions;
}
lastBit = currBit;
}
}
return transitions;
}
代码中首先是将现有的方块和容器合并,求出合并后的容器结果。接着枚举所有行,查看每一行的变换次数。算法很简单,只需要先记录上一次小方块的样式,将其存储到 lastBit 变量,接着查看当前的小方块样式,如果现在的和上一次不同,则转换加 1 ,查看后不要忘记更新 lastBit 。
8. 计算 Number of Holes
计算洞洞的个数,其实和计算 Row Transitions 方法类似,只不过这一次不再是记录变化的次数,而是记录真正空洞的个数。
//计算 Number of Holes
static int getNumberOfHoles(const Tetris* tetris, BlockType type, BlockState state, int column)
{
//合并
unsigned long container[TETRIS_CONTAINER_HEIGHT] = { 0 };
if (getMergedContainer(tetris, type, state, column, container) < 0) {
return -1;
}
//计算洞洞
int holes = 0;
unsigned long rowHoles = 0;
unsigned long prevRow = container[BLOCK_HEIGHT];
for (int i = BLOCK_HEIGHT+1; i < TETRIS_CONTAINER_HEIGHT - 1; i++)
{
//计算当前行洞洞位置
rowHoles = ~container[i] & (prevRow | rowHoles);
//统计
for (int j = 1; j < TETRIS_CONTAINER_WIDTH - 1; j++) { holes += ((rowHoles >> j) & 0x01);
}
prevRow = container[i];
}
return holes;
}
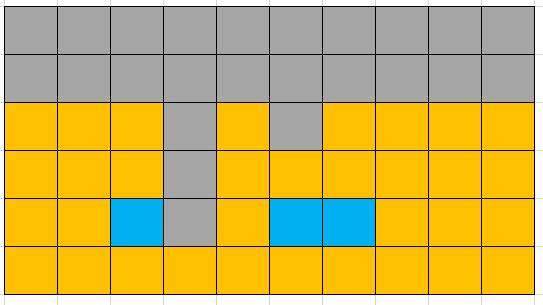
代码核心实际上就是双层 for 循环,枚举每一个位置,不过有一个 rowHoles 变量需要注意一下。这个变量表示上一行洞洞的情况,这个变量主要的作用是为了区分当前的遇见的空洞是否为真的空洞,如下图:
假设上面是容器最下方的截图,其中橙色是容器中已经有小方块的位置,其中灰色和蓝色是没有小方块的位置,而图中只有蓝色是真正的 “洞”。也就是说,同一个列,上一行有小方块的位置一下行才是洞。
9. 计算 Well Sums
计算“井”的方法很简答,就是要看当前列两边是否都有方块,且当前列是空的地方才算“井”。
//计算 Well Sums
static int getWellSums(const Tetris* tetris, BlockType type, BlockState state, int column)
{
//合并
unsigned long container[TETRIS_CONTAINER_HEIGHT] = { 0 };
if (getMergedContainer(tetris, type, state, column, container) < 0) {
return -1;
}
//计算井
int wellSums = 0;
for (int i = 1; i < TETRIS_CONTAINER_WIDTH - 1; i++)
{
for (int j = BLOCK_HEIGHT; j < TETRIS_CONTAINER_HEIGHT; j++) { if (((container[j] >> i) & 0x01) == 0
&& (container[j] >> (i + 1) & 0x01) == 1
&& (container[j] >> (i - 1) & 0x01) == 1
)
{
wellSums++;
for (int k = j + 1; k < TETRIS_CONTAINER_HEIGHT; k++) { if (((container[k] >> i) & 0x01) == 0) {
wellSums++;
} else {
break;
}
}
}
}
}
return wellSums;
}
这里需要记住,最后计算的不是“井”的深度,而是深度的累加和。
10. 计算最终得分
实现了上述 6 种特征的计算方法,接下来就是将这些特征值乘以一个比例系数,最终求和得到的就是最后的总分。
//计算 score
double evaluateScore(const Tetris* tetris, BlockType type, BlockState state, int column)
{
//计算第一个参数
double score = getLandingHeight(tetris, type, state, column);
if (score < 0) {
return INT_MIN;
}
score = score * -4.500158825082766;
//定义函数指针
int (*func[5])(const Tetris * tetris, BlockType type, BlockState state, int column) = {
getEliminatedRows,
getRowTransitions,
getColumnTransitions,
getNumberOfHoles,
getWellSums
};
//设定函数系数
double coeffs[5] = {
3.4181268101392694,
-3.2178882868487753,
-9.348695305445199,
-7.899265427351652,
-3.3855972247263626
};
for (int i = 0; i < 5; i++)
{
int ret = func[i](tetris, type, state, column);
if (ret < 0) {
return INT_MIN;
}
score += (ret * coeffs[i]);
}
return score;
}
11. 实现智能 AI
最后要想实现真正的智能,需要在每一次出现新方块的时候,计算出大方块最适合的下落位置。说白了就是枚举大方块所有的下落可能,然后求出分数最高的位置。
//获取推荐方块
void getRecommenderBlock(const Tetris* tetris, const Block* src, Block* dst)
{
assert(src && dst);
double scores[BS_NUM][TETRIS_CONTAINER_HEIGHT] = { 0 };
double maxScore = INT_MIN;
int col = 0;
dst->col = 0;
dst->row = 0;
dst->state = src->state;
dst->type = src->type;
//枚举原类型的所有形式
for (int i = 0; i < BS_NUM; i++)
{
//枚举所有位置
for (int j = 0; j < TETRIS_CONTAINER_HEIGHT; j++) { scores[i][j] = evaluateScore(tetris, dst->type, i, j);
if (scores[i][j] >= maxScore) {
maxScore = scores[i][j];
dst->state = i;
col = j;
}
}
}
//获取推荐方块属性
const AIBlock* props = getBlockProps(dst->type, dst->state);
assert(props);
//获取位置
dst->col = -props->leftSpare + col + 1;
while (!hitTest(dst, tetris)) {
moveDown(dst);
}
dst->row -= 1;
}
参数 src 代表当前大方块的位置,而最终计算的结果被保存在 dst 参数中。
到此为止,俄罗斯方块的智能 AI 系统算是实现完毕,下面可以看看运行效果,具体程序演示已经放到了下载页面: