机器学习入门 - 梯度算法
1. 梯度是什么?
梯度 : 一个向量,导数+变化最快的方向
机器学习:
收集数据x, 构建模型f,通过f(x, w) = Ypredict
判断模型质量的方法,计算loss
l o s s = ( Y p r e d i c t − Y t r u e ) 2 ( 回 归 损 失 ) l o s s = Y t r u e ⋅ l o g ( Y p r e d i c t ) ( 分 类 损 失 ) loss = (Y_{predict} - Y_{true})^2 \quad (回归损失)\\ loss = Y_{true}·log(Y_{predict}) \quad (分类损失) loss=(Ypredict−Ytrue)2(回归损失)loss=Ytrue⋅log(Ypredict)(分类损失)
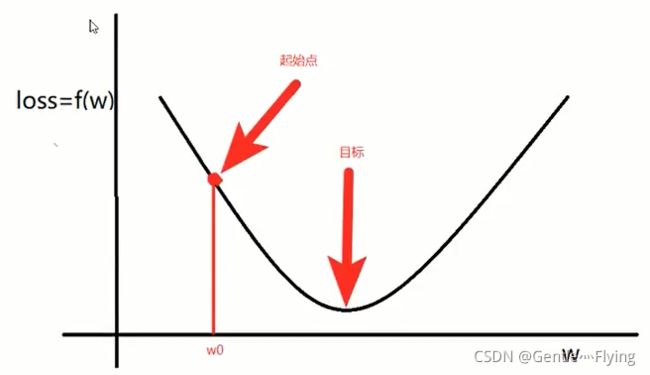
通过学习参数w,尽可能降低模型的loss,那我们应该如何调整w呢?
-
对w0点进行求导,求得梯度为:
Δ w = f ( w + x ) − f ( w ) x ( x → 0 ) \Delta w = \frac {f(w+x) - f(w)}{x} \quad (x \rightarrow 0) Δw=xf(w+x)−f(w)(x→0) -
更新w
w = w − α Δ w w = w - \alpha \Delta w w=w−αΔw
当 Δ w \Delta w Δw>0, 意味着w将增大,反之w将减小。
总结:梯度就是函数参数的变化趋势,若只有一个变量时,就是导数
2. 反向传播算法
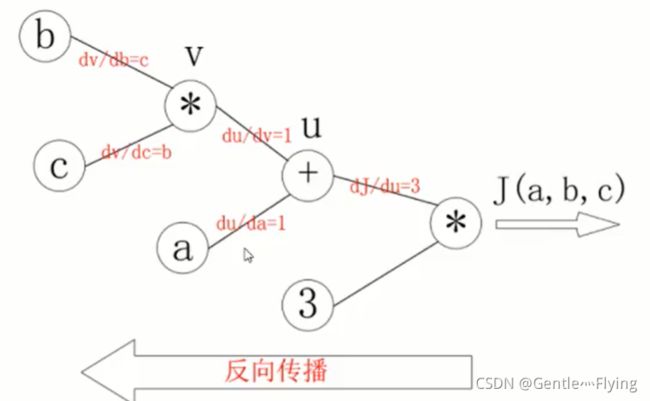
计算图和反向传播
通过计算图,我们可以轻易通过多个变量计算最后的结果 J(a, b, c),这也称之为向前计算。
其中,通过如图对各部分的导数的计算,我们可以轻易地获得任意变量之间的偏导
如:
d J d b = 3 × 1 × c d J d c = 3 × 1 × b \frac {dJ} {db} = 3\times 1\times c \quad \frac {dJ}{dc} = 3 \times 1\times b dbdJ=3×1×cdcdJ=3×1×b
3. 使用梯度算法实现线性回归
3.1 手动实现线性回归
案例分析:
- x为200 × \times × 1的矩阵,让y = x × \times × 3 + 0.8
- w, b初始化为任意数,用于计算获得原式子中的"3"和"0.8"
- 让y_predict赋值为 x × \times ×w+b, 计算出在该参数条件下预测出的y值
- 计算loss,并通过loss.backward()计算反向传播,从而获取各个参数的梯度。
- 通过公式 w = w − α Δ w w = w - \alpha \Delta w w=w−αΔw 计算出新的参数,并跳回第3步
代码演示:
import torch
import matplotlib.pyplot as plt
#1. y = 4x + 0.3
x = torch.rand([200, 1])
y = x * 3 + 0.8
learning_rate = 0.01;#设置学习率,即公式中的α
#2. 通过模型计算y_predict
w = torch.rand([1, 1], requires_grad=True) #require_grad为要求系统计算梯度,也即是纪录该计算图,才可以后面使用backward()进行反向传播
b = torch.tensor(0, requires_grad=True, dtype=torch.float32)
y_predict = y;
plt.figure(figsize=(20, 8)) #通过plt画图
for i in range(1000): #循环1000次训练
y_predict = torch.mm(x, w) + b
loss = (y - y_predict).pow(2).mean()
if w.grad is not None : #若梯度不空,则必须先对其置零操作,否则无法进行下一步的反向传播
w.grad.zero_()
if b.grad is not None :
b.grad.zero_()
loss.backward();
w.data = w.data - learning_rate*w.grad;
b.data = b.data - learning_rate*b.grad;
print("第" , i ,"次 循环: w ,b = ", w, " ", b)
if i == 0: ##画出第一条线,形状为点线,颜色为蓝色
plt.plot(x.numpy().reshape(-1), y_predict.detach().numpy().reshape(-1), 'b-.')
elif i % 100 == 0:#当为100的整数,画一条形状为虚线,颜色为黑色的线
plt.plot(x.numpy().reshape(-1), y_predict.detach().numpy().reshape(-1), 'k--')
print("结束时: w ,b = ", w, " ", b)
# print("结束时: y_predict = ", y_predict)
print("结束时: loss = ", loss)
y_predict = torch.mm(x, w) + b
plt.scatter(x.numpy().reshape(-1), y.numpy().reshape(-1))#画点,通过点描绘真实y的线
plt.plot(x.numpy().reshape(-1), y_predict.detach().numpy().reshape(-1), "r-") #画出最后一条预测线,颜色为红色,线为实线
plt.show() ##画线
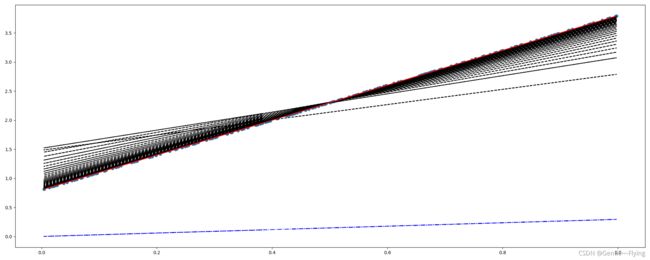
效果展示:
循环1000次时:
第 999 次 循环: w ,b = tensor([[2.5627]], requires_grad=True) tensor(1.0495, requires_grad=True)
结束时: w ,b = tensor([[2.5627]], requires_grad=True) tensor(1.0495, requires_grad=True) //跟原来的3x+0.8还是有很大差距的
结束时: loss = tensor(0.0149, grad_fn=)
其中: 最下面的蓝色点线,为第一次的预测y线;黑色线为第1次到999次的线,蓝色点线为真实值y线,红色线为最后一次的预测线;我们可以看到,随着训练数量的增加,预测y线越来越接近真实值y线
循环5000次时:
第 4999 次 循环: w ,b = tensor([[2.9958]], requires_grad=True) tensor(0.8021, requires_grad=True)
结束时: w ,b = tensor([[2.9958]], requires_grad=True) tensor(0.8021, requires_grad=True) //跟上面的1000次作对比,可以看到这次的参数已经很接近真实值了
结束时: loss = tensor(1.3419e-06, grad_fn=)
改变学习率为0.1, 循环1000次
第 999 次 循环: w ,b = tensor([[3.0000]], requires_grad=True) tensor(0.8000, requires_grad=True)
结束时: w ,b = tensor([[3.0000]], requires_grad=True) tensor(0.8000, requires_grad=True) //居然直接找到了精确值,实际上在第826次就找到了
结束时: loss = tensor(4.9771e-12, grad_fn=)
可以看到,通过增大学习率,使得模型更快地建立起来,只是在其他模型有可能会导致获取精确的模型。
3.2 pytorch的api实现线性回归
代码展示
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
x = torch.rand([200, 1])
y = x*3 + 0.8
# 1.定义模型,优化器类实例化,loss实例化
class Ln(nn.Module):
def __init__(self):
super(Ln, self).__init__()
self.linear = nn.Linear(1, 2) #分别为输入和输出的特征数,在本例子中为列数,它会自动为你申请参数
def forward(self, x):
out = self.linear(x)
return out
model = Ln()
y_pre = 0
optimizer = optim.SGD(model.parameters(), lr=0.01)
lossFun = nn.MSELoss() ##初始化回归损失函数
plt.figure(figsize=(20, 8))
param = 0
print("长度为 : ", len(list(model.parameters())))
for i in range(1000):
y_pre = model(x) #计算y预测值
loss = lossFun(y, y_pre) #计算损失
optimizer.zero_grad() #更新梯度为0
loss.backward() #反向传播计算梯度
optimizer.step() #通过梯度更新各个参数
param = list(model.parameters())
print("第" , i ,"次 循环: w ,b = ", param[0], " ", param[1])
if i == 0:
plt.plot(x.numpy().reshape(-1), y_pre.detach().numpy().reshape(-1), 'b-.')
elif i % 100 == 0:
plt.plot(x.numpy().reshape(-1), y_pre.detach().numpy().reshape(-1), 'k--')
print("结束时 w ,b = ", param[0], " ", param[1])
print("损失为 : " , lossFun(y, y_pre))
plt.scatter(x.numpy().reshape(-1), y.numpy().reshape(-1))
plt.plot(x.numpy().reshape(-1), y_pre.detach().numpy().reshape(-1), "r-")
plt.show()
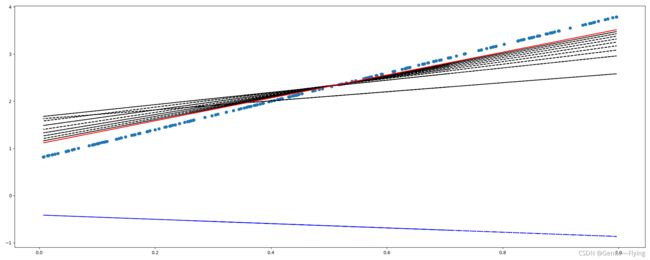
效果展示
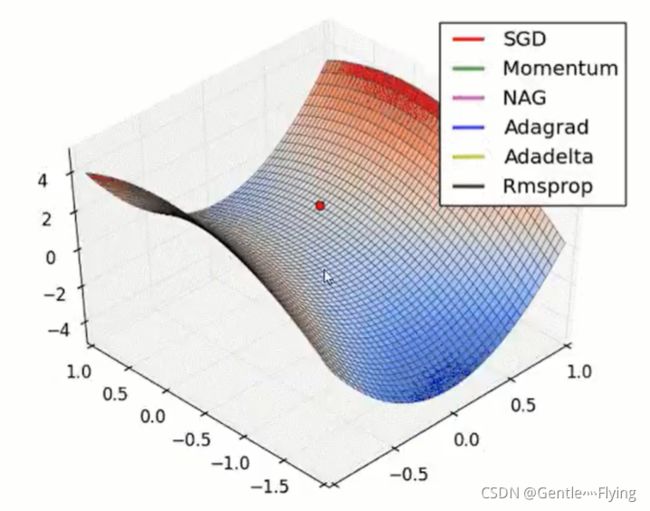
4. 常见优化算法
1. 梯度下降算法(batch gradient descent BGD)
每次迭代都将所有样本放入,这样每次迭代都顾及所有样本,做的是全局优化。
缺点: 速度慢,需要考虑所有样本
2.随机梯度下降法 (SGD)
从样本随机抽出一组,训练后更新一次,然后再抽取一组再更新一次,在样本量很大的情况下,可能不用训练完就可以获得损失值较小的模型了。
缺点:随机性强,但由于单个样本的训练可能带来很多噪声,往往会出现在开始训练时收敛的很快,训练一段时间之后变得很慢。
torch的api为:
torch.optim.SGD()
3. 小批量梯度下降(MBGD)
从样本抽取一小批进行训练,而不是一组,平均了速度和效果。
4. 动量法(Momentum)
小批量SGD虽然速度快,但是在最优点时难以精确,而是在最优点附近徘徊。
其次,另一缺点是小批量SGD需要我们挑选一个合适的学习率,当我们采用较小的学习率,会导致训练时收敛太慢;当我们使用较大的,就会导致训练时难以达到最优点。
基于梯度的移动指数加权平均,对网络的梯度进行平滑处理,让梯度的摆动幅度变得更小,更好地进入最优点
g = 0.8 g + 0.2 p r e g w 为 上 一 次 的 梯 度 w = w − α g α 为 学 习 率 g = 0.8g + 0.2preg \quad w为上一次的梯度 \\ w = w - \alpha g \quad \alpha为学习率 g=0.8g+0.2pregw为上一次的梯度w=w−αgα为学习率
w变化例子:(w为公式中的g,即为梯度)
5. AdaGrad
AdaGrad可以让梯度自适应学习,让梯度从大变小。
v = v + p r e V 2 w = w − α ( v + ∂ ) p r e V ∂ 为 小 常 数 , 为 了 数 值 稳 定 通 常 设 置 为 1 0 − 7 v = v + preV^2 \\ w = w - \frac \alpha {(v + \partial )} preV \quad \partial为小常数,为了数值稳定通常设置为10^{-7} v=v+preV2w=w−(v+∂)αpreV∂为小常数,为了数值稳定通常设置为10−7
由公式我们不难看出梯度(prev)会受到v的受到影响,而v会随着次数增多逐渐变大,梯度会随之逐渐下降,从而实现梯度的自适应。
6. RMSProp
进一步优化函数在更新函数摆动幅度过大的问题,让步长越来越小。
对参数的梯度使用了平方加权平均数。
7. Adam(Adaptive Moment Estimation)
将Momentum算法和RMSP算法结合的一种算法,防止梯度的摆幅过大,也能增快收敛速度。
torch的api为:
torch.optim.Adam()