A Survey on Graph Structure Learning: Progress and Opportunities
文章目录
-
- 摘要
- 引言
- 预备知识
-
- GSL pipline
- Graph Structure Modeling
-
-
- Metric-based Approaches
- Neural Approaches
- Direct Approaches
- Postprocessing Graph Structures
-
- Discrete Sampling
- Residual Connections
-
- Graph Regularization
-
-
- 稀疏性
- 平滑性
- 社区保持
-
摘要
图数据广泛用于描述现实中的实体及其他们之间的联系。图神经网络高度敏感于给定的图结构,因此噪声和不完备的图会得到不满意的表示并且妨碍模型全面理解潜在的机理。图结构学习GSL旨在联合学习最优的图结构和对应的图表示。在本篇工作中,我们广泛回顾了GSL最近的进展。
引言
图神经网络的成功归功于它同时探索了图结构和属性中的丰富信息,但是给定的图数据不可避免的会包含噪声和不完备,这样会阻碍GNN在现实问题中的应用。从表示学习的角度来讲,GNN是通过聚合邻居信息来学习节点表示的。这种迭代的方式存在一个级联的效果即当一个小的噪声传递给邻居节点后,许多其他的节点的表示质量也会下降。在一些工作中提到,对图结构的轻微攻击会导致GNN做出错误的预测。因此,对于GNN,高质量的图结构是必要的。
预备知识
G=(A,X)表示一个图,其中A为邻接矩阵,X为节点特征矩阵。图结构学习的目标是在给定一个图(可能不完备)后为确定的下游任务同时学习最优的邻接矩阵A*和对应的图表示Z。
graph generation目的是生成多个结构多样的图
graph learning目的是根据给定节点属性重建同质图的拉普拉斯矩阵
GSL pipline
经典的GSL模型包含两个部分:GNN编码器和结构学习器
1)GNN encoder输入为一张图,然后为下游任务计算节点嵌入
2)structure learner用于建模图中边的连接关系
现有的GSL模型遵从三阶段的pipline即1)graph construction, 2) graph structure modeling, 3) message propagation
Graph construction
最初给定的图结构是不完备的或者压根不可用,我们需要先构造一个初步的图作为起始点。其中构造方法有KNN graph,e近邻阈值构造等方法。
Graph structure modeling
GSL的核心是结构学习器。通过建模边的连接关系优化原始图。本文将现有的结构学习方法分为三类
- Metric-based approaches采用一个度量函数,输入节点对的嵌入来计算节点对之间的边的权重
- Neural approaches通过神经网络在给定节点表示条件下推测边的权重
- Direct approaches把邻接矩阵视作一个可学习的参数,在训练GNN是直接优化学习
不同于直接的方法,metric-based和neural approaches是通过一个参数化的网络来学习边的连接性的。输入节点的表示生成一个最优的关系矩阵A*。结构学习器生成的图结构还可以进一步采用一些后续的额外操作如离散采样等方法进一步获取最终的图结构。
Message propagation
在获得最优的图结构后,可以在该结构上使用图编码器聚合节点特征计算节点表示。
值得注意的是,很常见的一种方式是对后两个操作重复进行。也就是说,上一次更新的表示会接着用来建模边的权重,迭代的更新图的结构和节点表示。
Graph Structure Modeling
Metric-based Approaches
Metric-based方法采用核函数计算节点对的特征或者嵌入之间的相似性来作为边的权重。基于网络同质性假设,边倾向于连接相似的节点。这些方法通过提升类内的连接优化图的结构。

Gaussia kernels在AGCN中,首先计算每对节点特征的马氏距离,然后使用size为k的高斯核更新拓扑结构。其中M为对称的半正定矩阵
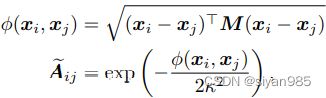
![]()
W是可训练的矩阵
Inner-product kernels使用边的两个端点的嵌入的内积建模边的权重
![]()
Cosine similarity kernels使用余弦相似度建模边的权重。其中w为可训练参数。
![]()
Diffusion kernels使用扩散核来建模边的连接性

![]()
其中θ是置信权重,T为广义转移矩阵。对于T的常见实现有个性化pagerank和heat kernel。
Fusion of multiple kernels同时使用多个kernel联合建图。
Neural Approaches
基于神经网络的方法在给定节点特征或者表示后使用深度神经网络建模边的权重。同时还可以引入注意力机制进一步捕获节点间复杂的交互关系。比如GAT在所有一阶邻居节点中使用自注意力机制计算邻居节点的权重。GAT的提升一条主线是设计不同的注意力机制,另一条是将类transformer的全注意力结构应用子图上。不同于只考虑局部邻居节点,Transformer是在所有节点上做信息传递只是把给定的图结构作为一个软的归纳偏置,这样可以挖掘一些新的关系。由于在信息传递时不再考虑图的连接关系,因此,图的位置和结构信息如何存储便成了Transformer-based方法的重要问题。
Direct Approaches
直接式方法是将目标图的邻接矩阵视作随机变量来学习的,并不依赖于节点的表示。大量的直接式方法使用图正则化来优化邻接矩阵的。这样显示的指定了最优图的属性。因为联合优化邻接矩阵和模型参数经常会引入不可导的操作,因此无法使用基于梯度的优化方法。一些工作将初始图结构和正则整合到混合的目标函数中,另外一些操作时整合低阶先验或者交替的优化邻接矩阵和学习参数。除了常见的正则器,GNNExplainer引入了一个基于互信息的可扩展的生成损失为最终任务识别最频繁的子图结构。还有一些工作是从概率的角度来建模邻接矩阵的即假设图的结构是从某个确定的分布中采样得到的。
Postprocessing Graph Structures
在一些工作中,对得到的图结构会使用一些后续的额外操作进一步优化图结构。常见的后处理步骤包含两个即离散采样和残差连接。
Discrete Sampling
GSL模型会使用一个采样步骤即假设提纯的图是从一个确定的离散分布中通过额外的采样过程生成的。不直接把邻接矩阵视作边的连接权重,而是采用额外的采样步骤恢复图的离散特性,给结构学习器更多的灵活性来控制最终图的属性如稀疏性。
需要注意的是从离散分布中采样是不可微的。除了先前在直接式方法中提到的特定优化方法外,我们讨论传统的梯度下降,通过使用复参数化方法允许梯度可以在采样操作中传递。一个常见的方法是Gumbel-Softmax,通过从Gumbel分布中采样生成不同的图。
Residual Connections
初始的图结构如果存在的话通常会在拓扑结构上携带一些先验信息。那么很自然就可以假设最优的图结构是从原始图中简单转化而来的。其中A为原始图结构,A~为学习到的图结构。
![]()
Graph Regularization
为了学到的图包含一些特定的属性,还需要引入图正则技术。
稀疏性
现实中的图数据往往包含噪声或者与任务不想关的边,我们通常需要在邻接矩阵上加一个稀疏性约束项。一种常用的方法是采用l0正则。但由于最小化l0正则是个NP难问题,所以往往用L1正则代替。还有一些隐式的稀疏化操作如在计算邻接矩阵相似度时设置阈值或者采用离散采样等操作确保学到的图的稀疏性。
平滑性
把节点特征矩阵的每一行视作图中的一个信号。在图信号处理中有一个重要假设为信号在邻接节点之间变化平缓。

社区保持
在现实图数据中,节点在不同的拓扑簇中会有不同的标签。因此,如果边跨越多个社区则会被视作噪声。根据图谱理论,邻接矩阵的阶数与途中连接的组件数量有关。低阶图包含稠密的连接组件。因此为去除噪声边,最大保留社区结构,一般引入低阶正则项。
