题目描述
这是 LeetCode 上的 749. 隔离病毒 ,难度为 困难。
Tag : 「模拟」、「图论搜索」、「BFS」
病毒扩散得很快,现在你的任务是尽可能地通过安装防火墙来隔离病毒。
假设世界由 $m \times n$ 的二维矩阵 isInfected 组成,isInfected[i][j] == 0 表示该区域未感染病毒,而 isInfected[i][j] == 1 表示该区域已感染病毒。可以在任意 $2$ 个相邻单元之间的共享边界上安装一个防火墙(并且只有一个防火墙)。
每天晚上,病毒会从被感染区域向相邻未感染区域扩散,除非被防火墙隔离。现由于资源有限,每天你只能安装一系列防火墙来隔离其中一个被病毒感染的区域(一个区域或连续的一片区域),且该感染区域对未感染区域的威胁最大且 保证唯一 。
你需要努力使得最后有部分区域不被病毒感染,如果可以成功,那么返回需要使用的防火墙个数; 如果无法实现,则返回在世界被病毒全部感染时已安装的防火墙个数。
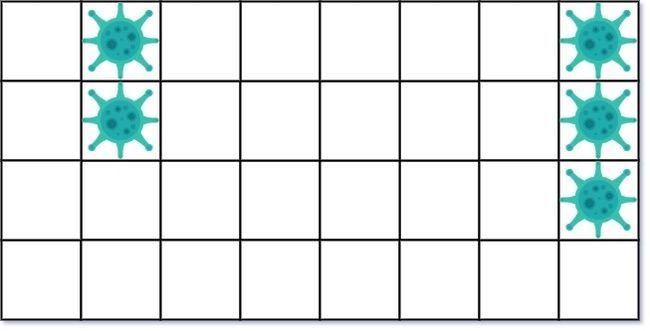
输入: isInfected = [[0,1,0,0,0,0,0,1],[0,1,0,0,0,0,0,1],[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0]]
输出: 10
解释:一共有两块被病毒感染的区域。
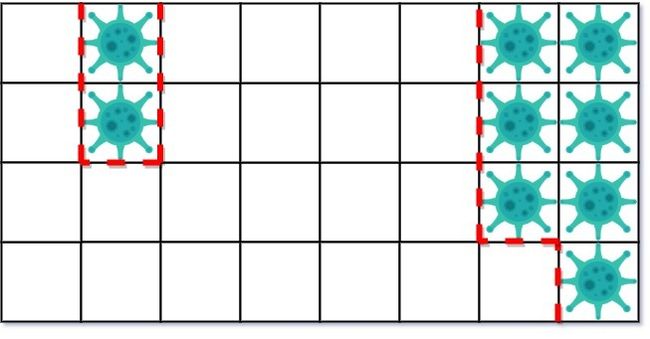
在第一天,添加 5 墙隔离病毒区域的左侧。病毒传播后的状态是:
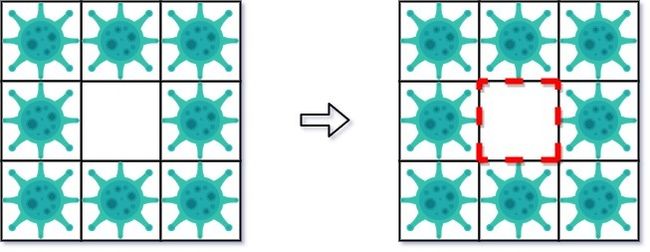
第二天,在右侧添加 5 个墙来隔离病毒区域。此时病毒已经被完全控制住了。输入: isInfected = [[1,1,1],[1,0,1],[1,1,1]]
输出: 4
解释: 虽然只保存了一个小区域,但却有四面墙。
注意,防火墙只建立在两个不同区域的共享边界上。示例 3:
输入: isInfected = [[1,1,1,0,0,0,0,0,0],[1,0,1,0,1,1,1,1,1],[1,1,1,0,0,0,0,0,0]]
输出: 13
解释: 在隔离右边感染区域后,隔离左边病毒区域只需要 2 个防火墙。提示:
- $m == isInfected.length$
- $n == isInfected[i].length$
- $1 <= m, n <= 50$
isInfected[i][j]is either0or1- 在整个描述的过程中,总有一个相邻的病毒区域,它将在下一轮 严格地感染更多未受污染的方块
搜索模拟
根据题意,我们可以按天进行模拟,设计函数 getCnt 用于返回当天会被安装的防火墙数量,在 getCnt 内部我们会进行如下操作:
- 找出当天「对未感染区域的威胁最大」的区域,并将该区域进行隔离(将 $1$ 设置为 $-1$);
- 对其他区域,进行步长为 $1$ 的感染操作。
考虑如何实现 getCnt:我们需要以「连通块」为单位进行处理,因此每次的 getCnt 操作,我们先重建一个与矩阵等大的判重数组 vis,对于每个 $g[i][j] = 1$ 且未被 $vis[i][j]$ 标记为 True 的位置进行搜索,搜索过程使用 BFS 实现。
在 BFS 过程中,我们除了统计该连通块所需要的防火墙数量 $b$ 以外,还需要额外记录当前连通块中 $1$ 的点集 s1(简称为原集,含义为连通块的格子集合),以及当前连通块相邻的 $0$ 的点集 s2(简称为扩充集,含义为将要被感染的格子集合)。
根据题意,在单次的 getCnt 中,我们需要在所有连通块中取出其 s2 大小最大(对未感染区域的威胁最大)的连通块进行隔离操作,而其余连通块则进行扩充操作。
因此我们可以使用两个变量 max 和 ans 分别记录所有 s2 中的最大值,以及取得最大 s2 所对应连通块所需要的防火墙数量,同时需要使用两个数组 l1 和 l2 分别记录每个连通块对应的「原集」和「扩充集」,方便我们后续进行「隔离」和「感染」。
Java 代码:
class Solution {
int[][] g;
int n, m, ans;
int[][] dirs = new int[][]{{1,0},{-1,0},{0,1},{0,-1}};
boolean[][] vis;
int search(int _x, int _y, Set s1, Set s2) {
int ans = 0;
Deque d = new ArrayDeque<>();
vis[_x][_y] = true;
d.addLast(new int[]{_x, _y});
s1.add(_x * m + _y);
while (!d.isEmpty()) {
int[] info = d.pollFirst();
int x = info[0], y = info[1];
for (int[] di : dirs) {
int nx = x + di[0], ny = y + di[1], loc = nx * m + ny;
if (nx < 0 || nx >= n || ny < 0 || ny >= m || vis[nx][ny]) continue;
if (g[nx][ny] == 1) {
s1.add(loc);
vis[nx][ny] = true;
d.addLast(new int[]{nx, ny});
} else if (g[nx][ny] == 0) {
s2.add(loc);
ans++;
}
}
}
return ans;
}
int getCnt() {
vis = new boolean[n][m];
int max = 0, ans = 0;
// l1: 每个连通块的点集 s2: 每个连通块的候选感染点集
List> l1 = new ArrayList<>(), l2 = new ArrayList<>();
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (g[i][j] == 1 && !vis[i][j]) {
// s1: 当前连通块的点集 s2: 当前连通块的候选感染点集
Set s1 = new HashSet<>(), s2 = new HashSet<>();
int b = search(i, j, s1, s2), a = s2.size();
if (a > max) {
max = a; ans = b;
}
l1.add(s1); l2.add(s2);
}
}
}
for (int i = 0; i < l2.size(); i++) {
for (int loc : l2.get(i).size() == max ? l1.get(i) : l2.get(i)) {
int x = loc / m, y = loc % m;
g[x][y] = l2.get(i).size() == max ? -1 : 1;
}
}
return ans;
}
public int containVirus(int[][] _g) {
g = _g;
n = g.length; m = g[0].length;
while (true) {
int cnt = getCnt();
if (cnt == 0) break;
ans += cnt;
}
return ans;
}
} TypeScript 代码:
let g: number[][] = null
let n: number = 0, m: number = 0
let vis: boolean[][] = null
const dirs: number[][] = [[1,0],[-1,0],[0,1],[0,-1]]
function dfs(_x: number, _y: number, s1: Set, s2: Set): number {
let he = 0, ta = 0, ans = 0
let d: Array = new Array()
s1.add(_x * m + _y)
vis[_x][_y] = true
d[ta++] = _x * m + _y
while (he < ta) {
const poll = d[he++]
const x = Math.floor(poll / m), y = poll % m
for (const di of dirs) {
const nx = x + di[0], ny = y + di[1], loc = nx * m + ny
if (nx < 0 || nx >= n || ny < 0 || ny >= m || vis[nx][ny]) continue
if (g[nx][ny] == 1) {
s1.add(loc)
vis[nx][ny] = true
d[ta++] = loc
} else if (g[nx][ny] == 0) {
s2.add(loc)
ans++
}
}
}
return ans
}
function getCnt(): number {
vis = new Array>(n)
for (let i = 0; i < n; i++) vis[i] = new Array(m).fill(false)
let max = 0, ans = 0
let l1: Array> = new Array>(), l2: Array> = new Array>()
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (g[i][j] == 1 && !vis[i][j]) {
let s1 = new Set(), s2 = new Set()
const b = dfs(i, j, s1, s2), a = s2.size
if (a > max) {
max = a; ans = b
}
l1.push(s1); l2.push(s2)
}
}
}
for (let i = 0; i < l2.length; i++) {
for (let loc of l2[i].size == max ? l1[i] : l2[i]) {
const x = Math.floor(loc / m), y = loc % m
g[x][y] = l2[i].size == max ? -1 : 1
}
}
return ans
}
function containVirus(_g: number[][]): number {
g = _g
n = g.length; m = g[0].length
let ans: number = 0
while (true) {
const cnt = getCnt()
if (cnt == 0) break
ans += cnt
}
return ans
}; - 时间复杂度:最多有 $n + m$ 天需要模拟,每天模拟复杂度 $O(n \times m)$,整体复杂度为 $O((n + m) \times nm)$
- 空间复杂度:$O(nm)$
最后
这是我们「刷穿 LeetCode」系列文章的第 No.749 篇,系列开始于 2021/01/01,截止于起始日 LeetCode 上共有 1916 道题目,部分是有锁题,我们将先把所有不带锁的题目刷完。
在这个系列文章里面,除了讲解解题思路以外,还会尽可能给出最为简洁的代码。如果涉及通解还会相应的代码模板。
为了方便各位同学能够电脑上进行调试和提交代码,我建立了相关的仓库:https://github.com/SharingSou... 。
在仓库地址里,你可以看到系列文章的题解链接、系列文章的相应代码、LeetCode 原题链接和其他优选题解。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地
本文由mdnice多平台发布