《PyTorch深度学习实践》学习笔记：卷积神经网络（高级篇）

---

1.串行的网络结构

之前的网络，不管是全连接神经网络还是卷积神经网络，都是一种串行的结构。

2. GooleNet

2.1 结构分析

GooleNet的网络结构，里面的模块称为inception。

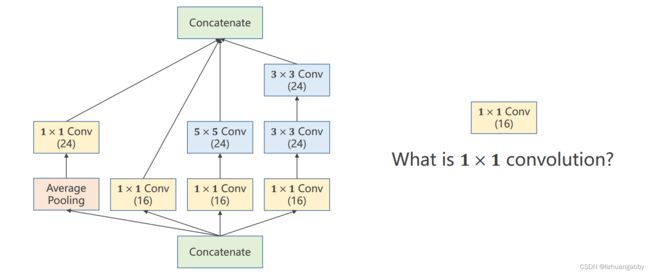
inception模块的构成方式其实有很多种，这只是其中的一种，首先需要知道inception为什么这样构建？
因为构建的时候有一些超参数是比较难选的，比如卷积核的大小，是使用3x3，还是5x5还是使用其他的方式，GooleNet的出发点就是不知道哪个卷积核好用，那么就在一个块里面把卷积核都使用一下，然后把他们结果挪到一起，之后如果3x3的好用，自然3x3的权重就会变得比较大，其他路线的权重相对就会变得更小，所以这是提供了几种后续的神经网络的配置，然后通过训练自动的找到最优的卷积的组合，这是GooleNet设计的灵感。

Concatenate：把张量拼接到一块。4条路径算出来4个张量，所以肯定要做一个拼接。

Average Pooling：均值池化，4条分支后续要进行拼接，所以必须要保持他们的宽度和高度是一致的，输出的图像格式为（B,C,W,H），唯一可以不同的就是C（channel），不同的卷积核为了使得输出的W和H一致，可以通过padding来实现。
之前使用的是2x2的最大池化，导致图像变成了原来的一半，所以解决方案是做池化的时候认为的指定stride=1，padding= 多少，例如使用3x3的大小去做均值，可以使用padding=1，有点类似卷积的操作，但是没有卷积核，使用的可以称为均值卷积核，卷积核中的数都一样，所以均值池化可以通过设置stride和padding使得输入输出图像的大小是一致的。

1x1的卷积：代表卷积核大小就是1x1的，1x1卷积的个数取决于输出张量的通道数。

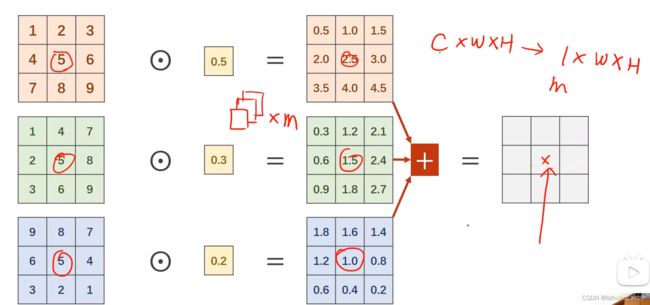
1*1卷积完成了一个信息融合。
所以1x1卷积最主要的工作：改变通道数，减小复杂度。

神经网络里面的问题就是运算量太大，所以我们需要思考怎么解决运算量大的问题。

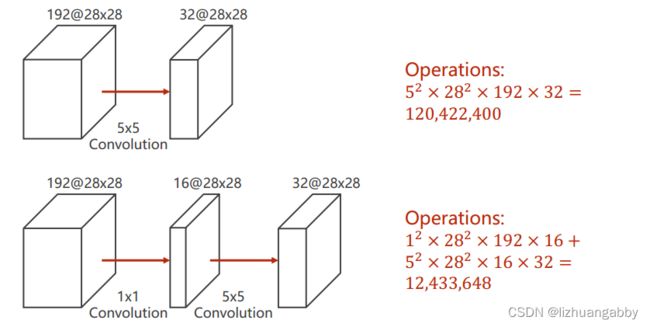
在原来的基础上添加了一层1x1的卷积层之后，运算量变为了原来的1/10。

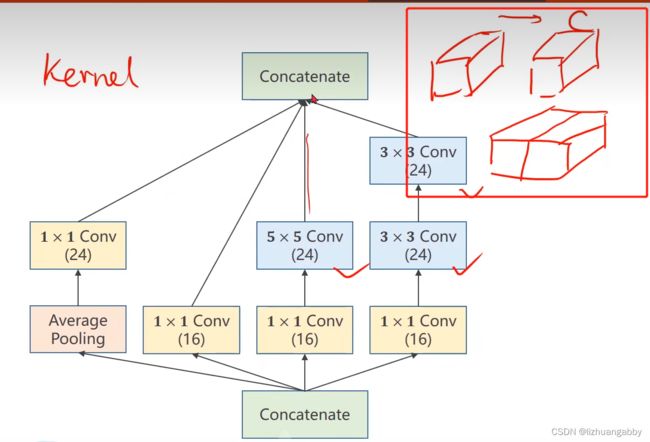
inception到底怎么实现？

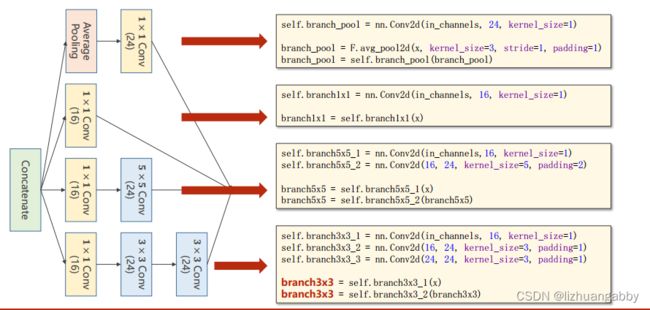
上图最后一行少了branch = self.branch3x3_3(branch3x3)，因为ppt写不下了）

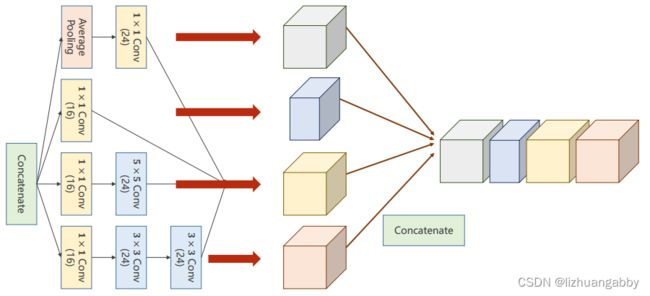
在各个计算完成之后还需要拼接，按照各个通道进行拼接，图示化如下：


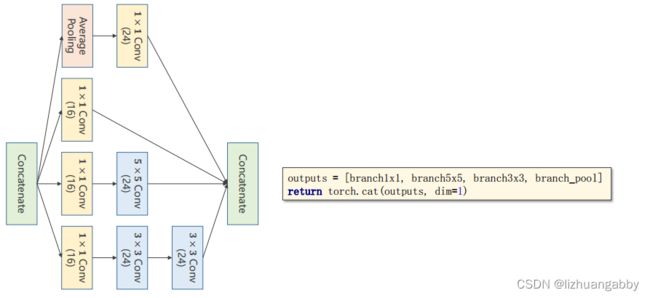
dim=1，因为我们输入的图像是（B,C,W,H），dim=1就代表C，按照通道进行拼接。
上图中，我们可以计算出输出通道数为24+16+24+24=88

2.2 代码实现

# inception模块
class Inception(nn.Module):
    def __init__(self,in_channels):
        super(Inception, self).__init__()
        self.branch1x1 = nn.Conv2d(in_channels,16,kernel_size=1)

        self.branch5x1 = nn.Conv2d(in_channels,16,kernel_size=1)
        self.branch5x2 = nn.Conv2d(16,24,kernel_size=5,padding=2)

        self.branch3x1 = nn.Conv2d(in_channels,16,kernel_size=1)
        self.branch3x2 = nn.Conv2d(16,24,kernel_size=3,padding=1)
        self.branch3x3 = nn.Conv2d(24,24,kernel_size=3,padding=1)

        self.branch_pool = nn.Conv2d(in_channels,24,kernel_size=1)

    def forward(self,x):
        branch1x1 = self.branch1x1(x)

        branch5x5 = self.branch5x1(x)
        branch5x5 = self.branch5x2(branch5x5)

        branch3x3 = self.branch3x1(x)
        branch3x3 = self.branch3x2(branch3x3)
        branch3x3 = self.branch3x3(branch3x3)

        branch_pool = f.avg_pool2d(x,kernel_size = 3,stride = 1,padding = 1)
        branch_pool = self.branch_pool(branch_pool)

        outputs = [branch1x1,branch5x5,branch3x3,branch_pool]
        return torch.cat(outputs,dim=1)  # 按通道进行拼接

注意初始的输入通道没有写死，而是作为in_channels入参设置。

# 网络模块
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Conv2d(1,10,kernel_size=5)
        self.conv2 = nn.Conv2d(88,20,kernel_size=5)

        self.incep1 = Inception(in_channels=10)
        self.incep2 = Inception(in_channels=20)

        self.mp = nn.MaxPool2d(2)
        self.fc = nn.Linear(1408,10)

    def forward(self,x):
        in_size = x.size(0)
        x = f.relu(self.mp(self.conv1(x))) # 10通道
        x = self.incep1(x)                 # 10通道变88通道
        x = f.relu(self.mp(self.conv2(x))) # 88通道变20通道
        x = self.incep2(x)                 # 20通道变88通道
        x = x.view(in_size,-1)             # 这里可以计算出拉成一维以后的大小
        x = self.fc(x)
        return x

还是在之前的MNIST数据集上进行测试Inception网络模型，观察测试的结果：


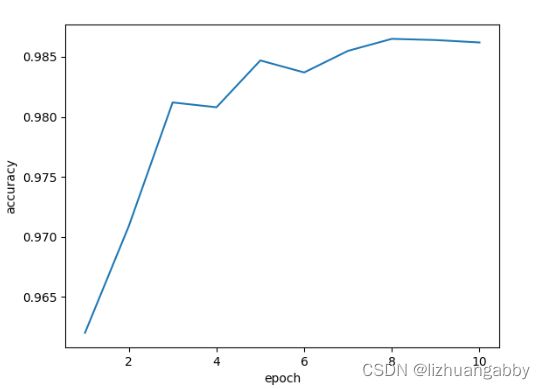
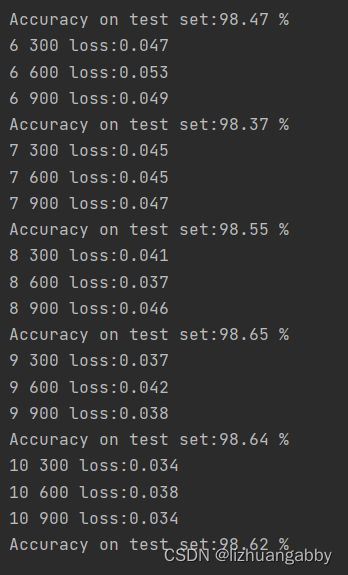
这里性能提高不多，主要原因还是背后的全连接层，不过我们重点看的是改变卷积层的结构来提高性能。此外，我们观察结果图可以发现，准确率上升到最高点后出现了下降，一般我们在训练的过程中，我们会保存我们每个epoch训练的结果，最后我们会在测试集上选用准确率高的训练模型。我们需要注意的是不是说训练的次数越多，网络的性能越好，训练的多了可能出现过拟合，导致模型的泛化能力变差。

3. ResNet

3.1 网络分析

出发点：把3x3的网络一直堆下去，性能会不会变好。实验发现，层数越多，反而错误率越高。

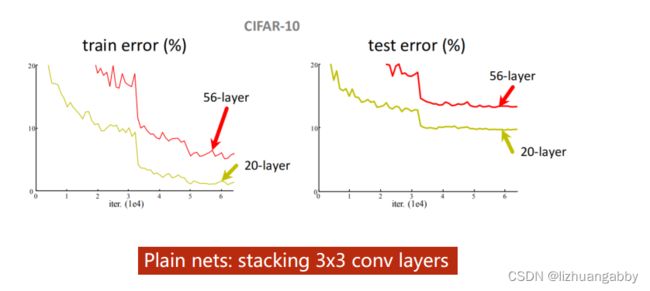
思考可能的原因：梯度消失，因为我们的网络会进行反向传播，而反向传播的本质是链式法则，假如一连串的梯度是小于1的，这样乘起来就会越来越小，最终趋近于0。
而我们的权重更新是：w = w - 学习率*梯度，如果梯度接近0了，那么他们的权重w就基本得不到什么更新。

解决梯度消失的问题：

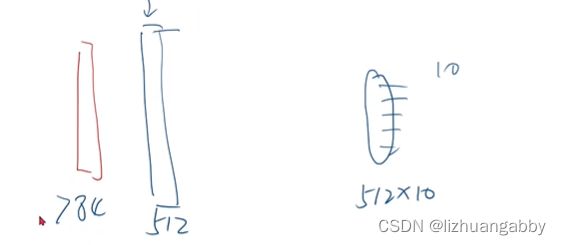
假如有一个512的隐藏层，然后后面直接接一个512x10的层进行训练，训练完成以后，把512层进行冻结;

然后再添加一个256的层，后面接256x10进行训练，训练完成以后，还是对256层进行加锁，逐层的进行训练。
通过以上这种训练方式来解决梯度消失的问题。但是在深度学习里面，这样做的话其实是一件很困难的事情，因为深度学习的层数是非常多的。

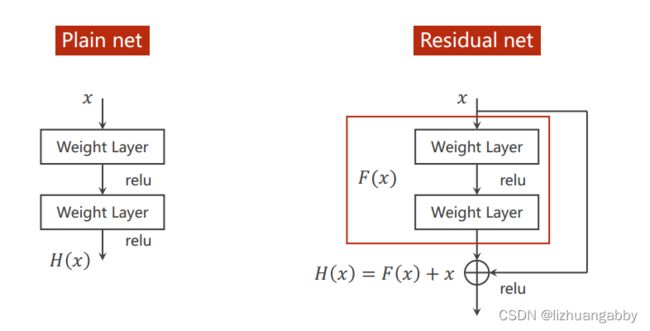
ResNet 引入残差结构最主要的目的是解决网络层数不断加深时导致的梯度消失问题。

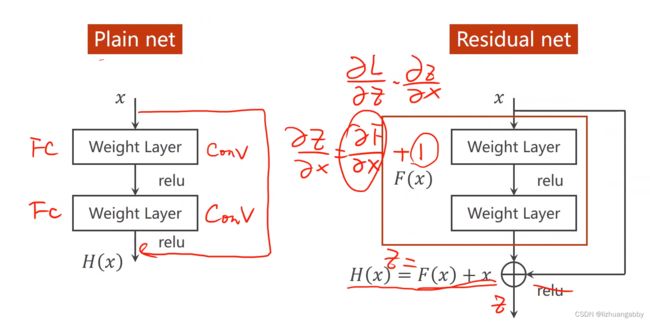
通过短路连接，可以实现在计算梯度的时候不至于接近0，而是梯度小的时候，计算的梯度值在1附近，这就是Resnet网络的智慧所在。

3.2 代码实现

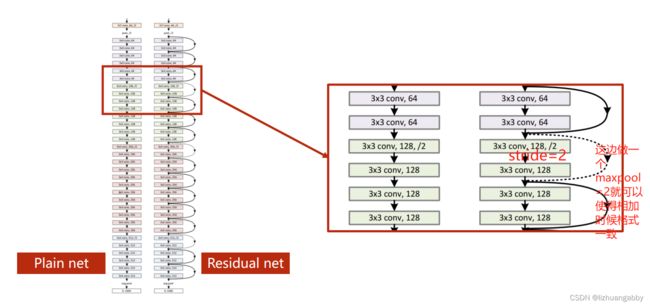
残差模块代码实现：

# ResiduaBlock模块
class ResiduaBlock(nn.Module):
    def __init__(self,channels):
        super(ResiduaBlock, self).__init__()
        self.channels = channels
        self.conv1 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
        self.conv2 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
    def forward(self,x):
        y = f.relu(self.conv1(x))
        y = self.conv2(y)
        return f.relu(x+y)

网络结构代码实现：

# 网络模块
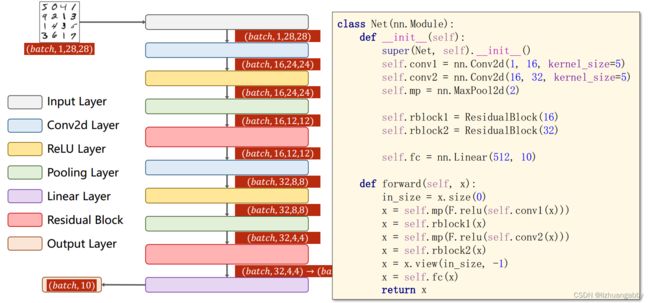
class Model(nn.Module):
    def __init__(self):
        super(Model, self).__init__()
        self.conv1 = nn.Conv2d(1,16,kernel_size=5)
        self.conv2 = nn.Conv2d(16,32,kernel_size=5)
        self.mp = nn.MaxPool2d(2)

        self.rblock1 = ResiduaBlock(16)
        self.rblock2 = ResiduaBlock(32)

        self.fc = nn.Linear(512,10)

    def forward(self,x):
        in_size = x.size(0)
        x = self.mp(f.relu(self.conv1(x)))
        x = self.rblock1(x)
        x = self.mp(f.relu(self.conv2(x)))
        x = self.rblock2(x)
        x = x.view(in_size,-1)
        x = self.fc(x)
        return x

还是以MNIST数据集为例，观察识别的结果：


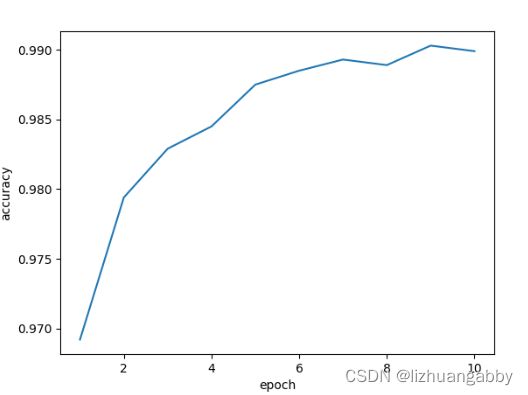
使用Residual network在测试集上的准确率为99%。

4. 练习

4.1 Reading Paper and Implementing ResNet

应用其它的Residual Block

ref：He K, Zhang X, Ren S, et al. Identity Mappings in Deep Residual Networks[C]

上图的第一种ResiduaBlock模块代码实现：

# 其他的ResiduaBlock模块
class ResiduaBlock(nn.Module):
    def __init__(self,channels):
        super(ResiduaBlock, self).__init__()
        self.channels = channels
        self.conv1 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
        self.conv2 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
    def forward(self,x):
        y = f.relu(self.conv1(x))
        y = self.conv2(y)
        return f.relu((x+y)*0.5)

运行结果：


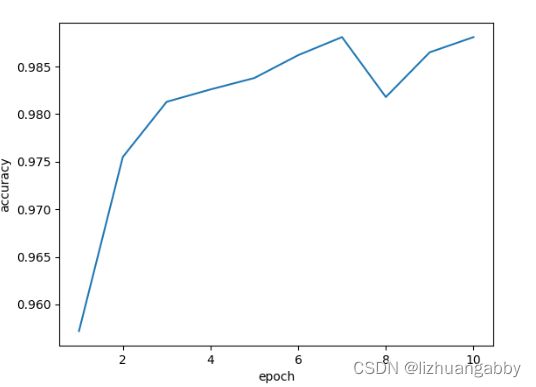
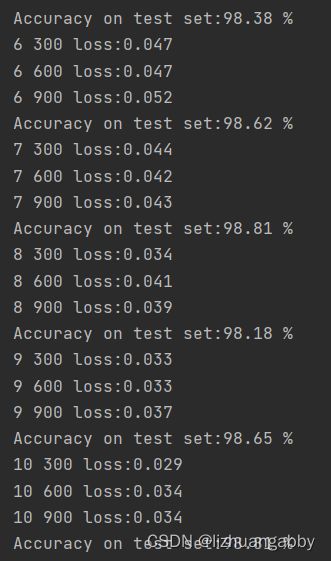
上图的第二种ResiduaBlock模块代码实现：

class ResiduaBlock(nn.Module):
    def __init__(self,channels):
        super(ResiduaBlock, self).__init__()
        self.channels = channels
        self.conv1 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
        self.conv2 = nn.Conv2d(channels,channels,kernel_size=3,padding=1)
        self.conv3 = nn.Conv2d(channels,channels,kernel_size=1)
    def forward(self,x):
        y = f.relu(self.conv1(x))
        y = self.conv2(y)
        z = self.conv3(x)
        return f.relu((z+y))

上述两种Residual Block都出现了明显的下降然后再上升。

更多的Residual Block细节可以去阅读一下Resnet原文以及Identity Mappings in Deep Residual Networks原文。

4.2 Reading and Implementing DenseNet

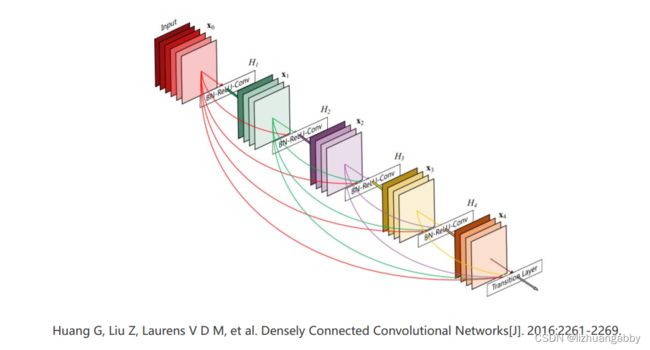
ref：Huang G, Liu Z, Laurens V D M, et al. Densely Connected Convolutional Networks[J]. 2016:2261-2269
应用DenseNet网络，上一层的输出不仅提供给下一层，甚至下面几层。

DenseNet后续阅读原文的时候去进行实现。

5. 总结

1. 学习理论《深度学习花书》
2. 写复杂的网络，阅读pytorch文档（至少通读一遍）
3. 复现经典的工作（读代码，训练架构，测试架构，数据构建，损失函数和优化器的构建；读代码后续写代码）（找到论文——读代码——写代码——读代码——写代码…）
4. 扩充视野，看到网络结构图能够明白怎么代码实现。选一个特定领域，大量阅读论文，看看常用技巧，想各种创新点。（提前是拥有前几步的能力）

后续还需要完成的工作：
1.泰塔尼克号网络的改进
2.多分类问题的kaggle实现
3.desnet的阅读与实现
4.其他经典工作的复现