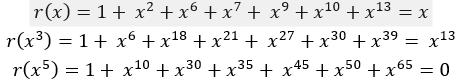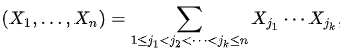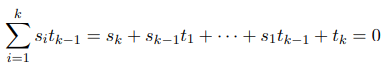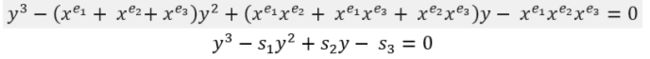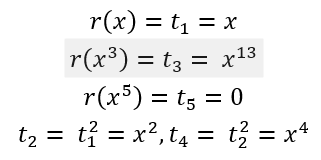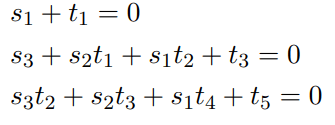BCH码(BCH code)详细分析

在信息论中，BCH codes 是指 Bose–Chaudhuri–Hocquenghem codes，可以用来纠错。BCH码利用了多项式一些很好的性质。本文将从0开始，用详细的例子解释二进制域中的BCH码。

二进制域与多项式

首先考虑二进制域，即所有每个位的取值只能是0或1。我们可以尝试把二进制数表示为多项式，二进制数中的从左往右第j位，是多项式x^j的系数。例如11011，可以表示成为 。

二进制域的四则运算与我们常见的十进制差不多，但由于在二进制1 + 1 = 2 = 0，所以我们每次计算后相当于模上2。例如计算11*11，在多项式表示就是  。这儿的x的系数2在二进制中等于0。另外很重要的概念就是二进制域中，加等于减，例如  相当于  。

寻找新的编码方式

我们先回顾简单的奇偶校验码和hamming码。简单的奇偶校验码只能检查出错误而不知道具体是哪里出错，而hamming码只能纠正一位错误。因此我们想能不能有一种方法可以纠正多位错误呢？

此时，多项式的威力就发挥了出来。假如我们的真正的消息是m(x)，然后乘上一个编码多项式p(x)，得到m(x)p(x)再将其发送过去。发送过程中会会受到很多干扰，于是多项式被加上错误多项式e(x)，而接收者接收者的消息为c(x)，就有

接收者怎么知道消息有没错呢？接收者事先就会和发送者商量好p(x)，然后就很简单，只要让c(x)除以p(x)，如果余项是0，即没有e(x)，没有受到干扰，那么商就是m(x)，就是正确的消息。如果余项不是零，我们的商就变成了m(x) + e(x)/p(x)，无法将真正的消息分离出来。

上述方法有个前提，在m(x) + e(x)/p(x)，p(x)必须是不可约的本原多项式(primitive polynomials)，这样才能让e(x)不被除尽，我们才能意识到有干扰的存在。至于如何寻找素多项式，将在之后说明。

纠单个错的例子

下面来看个例子。例如我们要发送的消息m(x)是1001，而编码多项式p(x)是1101，于是我们要发送出去的消息就是1100101。假如接收者也接收到了这个消息，用p(x)除后余项是0，没有错误存在，商是1001，就是发送者发送的消息，自然皆大欢喜。

但如果发送过程中，有一个位被某种不可抗拒的神秘力量改变了，变成了1100111，接收者同样用p(x)去除，得到了余项1110000，这下不好了，接收者知道出错了。但现在怎么去找出错误多项式e(x)呢？

我们知道，这个余项1110000，就是e(x)/p(x)的余项。为了找出e(x)，我们可以反过来推。于是制作一张表格

表格右侧就是如果出现一位错误，r(x)/p(x)后，e(x)/p(x)的余项。通过寻找余项结果，我们可以快速定位究竟是哪里出错了。当然如果e(x)为0，那么e(x)/p(x)的余项也为0。

上面这个方法之所以能奏效，对于所有的可能的错误。是因为右边的每一个余项都不相同，我们才不至于混淆。如果我们把p(x)换成10001会发生什么呢？这里10001不是本原多项式，因为10001可以分解成101乘101。

我们可以看到，右侧重复了！假如我们得到余项1000000，我们无法知道e(x)究竟是第一行的1000000还是第五行的0000100。

而本原多项式就好在，在所有错误余项e(x)出现前前，e(x)/p(x)的余项不会重复。之后将开始重复，这就是被称为循环（cyclic）码的原因。

寻找本原多项式

本原多项式是个神器，但哪些是本原多项式呢？首先有一些原则：

• r次多项式，最高次项x^r的系数必须是1。
• 多项式如果不包含常数项1，就会被x整除。
• 多项式项数不能是偶数的，比如  有四项，很容易将其分解为 。
• 每一项的次数也不能都是偶数，否则将每一项次数减半就能得到因子。例如  。

于是我们很容易找到：

按照上述方法还可以继续寻找更多的本原多项式。次数越高数量越多。

BCH码

但如果想要纠正多个错误呢？此时仅一个编码多项式p(x)就不够了，我们还需要更多的编码多项式来让我们能找出多个错误。这时就轮到BCH码出场了，其编码多项式标准形式是：

其中p(x)是本原多项式，而  都是可以被p(x)除余0的多项式。即

如果我们要设计一个可以纠正两个错误的编码多项式，就让  。要设计一个可以纠正三个错误的编码多项式，就让  。现在我们先说如何寻找  。

例如  。我们发现  ，所以  。我们用  代替  ，就得到  。

纠正多个错误的例子

注：以下计算均是模上了  的在二进制域内的计算。

还是和原来一样，假如我们要发生的消息m(x)是11010，选择的本原多项式是  ，那么  ，  。编码多项式就是   ，表示成二进制是11101100101，再乘上消息m(x)就是100001110110010，就是我们发送的出去的。

但现在接收者受到的r(x)却是 101000110110010。然后接收者开始计算：

前两项余项不为0，而第三项为0说明接到的只有两处错误。但如何把它们的位置找出来？我们就要用到错误定位多项式（ error locator polynomial ）了。即：

不过这时  可以认为是无穷小，这样  就是0。

如果我们能找到这个函数的两个根，我们也就找到了e1和e2。为了解决这个问题，我们得先定义两个函数。

两个函数

初等对称函数(Elementary symmetric polynomial)s，即满足下列的形式的多项式

另定义幂和对称函数（ power sum symmetric functions）t，

在我们的例子中，可能有三个错误，于是可表示成：

重点来了。我们有s与t的关系：

计算

此时上面的错误定位不等式就可以用s函数来描述：

我们知道一些t的结果：

再用s和t的关系计算

即第一个错误在第三个位，第二个错误在第六个位，没有第三个错误。于是将 101000110110010 修改回来得 100001110110010 ，再除Q(x)就得到了真正的消息m(x) = 11010 。

结语

BCH码被用于卫星通信，固态硬盘等领域。

例如BCH(31,16)码，每组有31个位，其中有效的信息位为16个，汉明距离为7，可以纠正3个位的错误。此时应该使用的本原多项式的最高项次数应该是5，因为  。

有时候我们使用可以用BCH纠正k个错误的码，但如果错误不止k个，我们就无法恢复正确的消息。但我们仍然可以恢复一些可能是正确的消息，再逐一排查。

延庆川北小区45号孙老师 东屯 收卖废品破烂垃圾炒股

whaosoft aiot http://143ai.com

额很多图片没有传上出哦 见谅