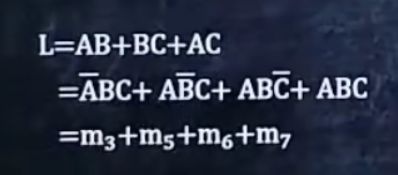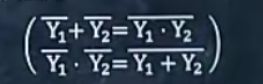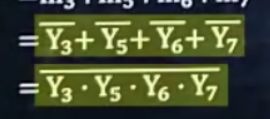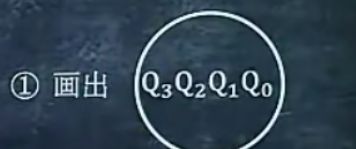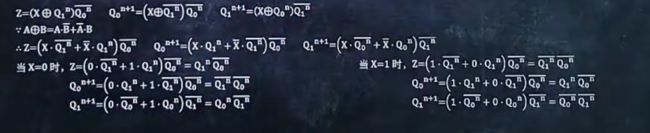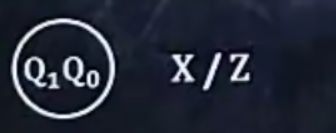【数字电路】期末不挂科复习笔记

【数字电路】期末不挂科复习笔记

数制与码制

1、将二进制转为十进制

从小数点向左，依次乘2的0次方，1次方…依次类推

2、将十进制转为二进制

将整数部分和小数部分分别转换即可

3、将二进制转为八进制

二进制先转十进制，再转八进制

4、将八进制转为二进制

八进制转十进制，再转二进制

5、将二进制转为十六进制

从小数点开始，四个一组，转为十进制

6、将十六进制转为二进制

十六进制先转为十进制，再转二进制

凑够四位，不够补0

总结

余3码就是8421码＋3

数字信号：

高电平是1，低电平是0

补码：

正数的源码和补码、反码都一样

负数的补码是反码＋1，负号是最前面1，正好是最前面0

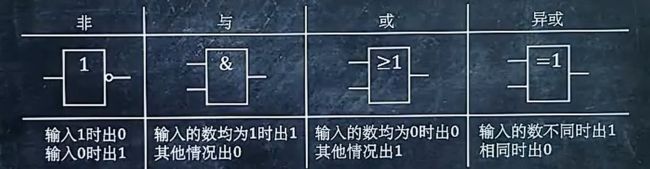
门电路

记住：同或和异或就是取非关系

三种基本门电路：与或非

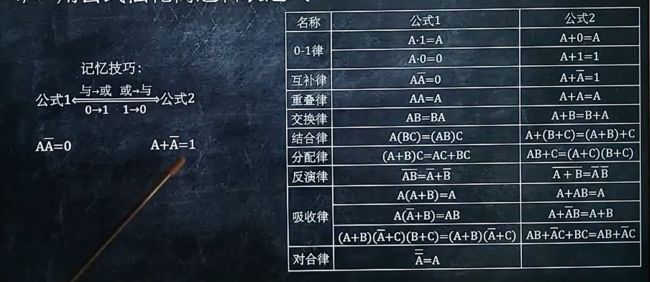
1、公式法化简

2、公式法将逻辑函数变成最小项的形式

前提是记住所有的公式！！！

逻辑图

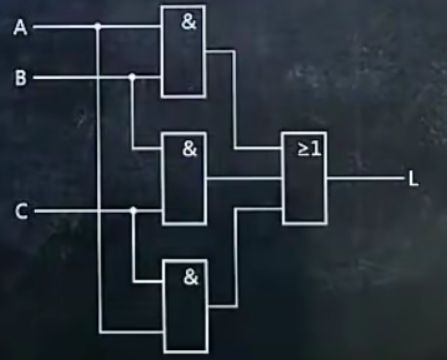
1、给出逻辑电路图，分析逻辑功能

设一个中间变量

然后化简

然后列出所有情况

然后分析电路

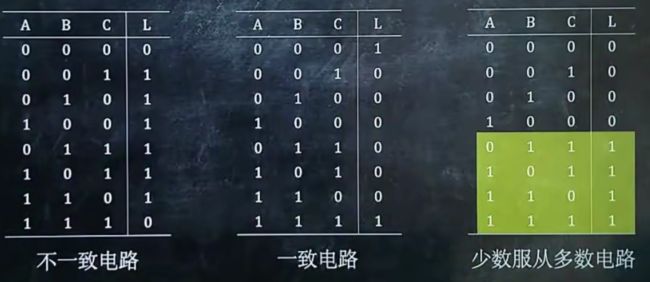
只有abc相同的时候是0，其他都是0，所以是“不一致电路”

三种常考的电路

2、给出功能要求，然后设计电路

最后画出电路图

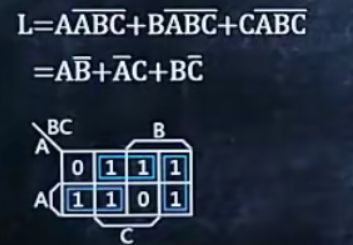
卡诺图

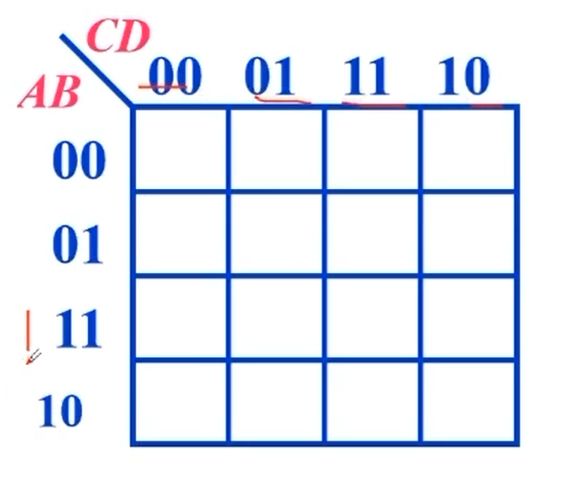
1、画卡诺图

位置不能错

​ 00 01 11 10

00

01

11

10

卡诺图的一项中的未知变量用x代替，x可以是0或1

得到

n个变量就有n个逻辑相邻项，每一个地方取反即是其中之一

先画卡诺图

在画卡诺圈，先找8个一起的1，再找4个，再找2个，最后找不到就找1个，直到所有的1都被使用过

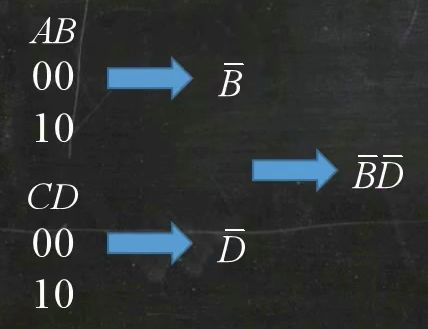
01就舍去

00就取反

11就不变

将得到的行列相与

最后将得到的多个相或

无关项：

d表示无关项

用x表示

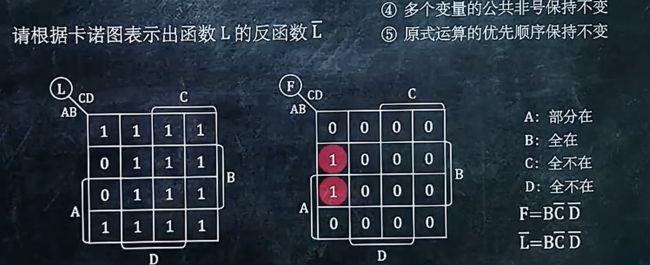
2、卡诺图求反函数

取反函数

直接画一个新的卡诺图，在原来的卡诺图基础上，0变1，1变0

3、用卡诺图法将逻辑函数变成最小项的形式

4、将最小项的形式化成变量形式

最后别忘了化简！

4变量也是一样的！

5、将L = m + d形式的式子用卡诺图化简

m是最小项，d是无关项，最后用卡诺图化简即可

译码器

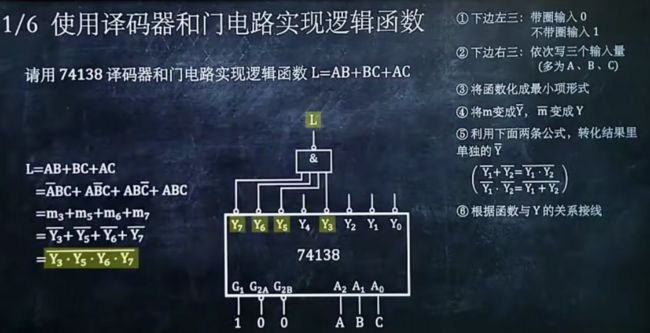
1、使用译码器和门电路实现逻辑函数

1.下边左三：带圈输入0，不带输入1

2.下边右三：一次写三个输入量，（A、B、C）

3.将函数化为最小项形式

4.将m变成Y非，m非变成Y

5.利用下面两条公式，转化结果为单独的Y非（德摩根定律）

得到

6.根据函数与Y 的关系接线

如图是3、5、6、7接线，接一个与非门

过程总览：

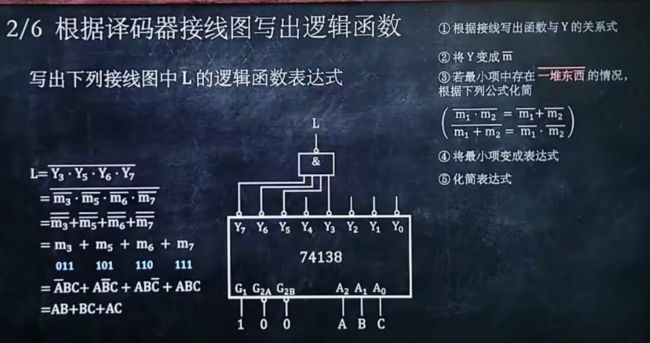
2、根据译码器接线图写出逻辑函数

1.根据接线写出函数与Y的关系式

2.将Y变成m非

3.若最小项中存在非了一堆东西的情况下，根据（德摩根定律）化简

4.将最小项变成表达式

5.化简表达式

3、使用8选1数据选择器实现3输入逻辑函数

1.下边左一：若带圈则接地/输入0；若不带圈则输入1

2.下边中三：一次写三个输入量（A.B.C）

3.将函数化为最小项形式

4.将m变成D

5.下边：将上步骤出现的D引出来接1，没出现的D引出来接0

6.上边：Y输出的是⑤中接1的D相或；Y非输出的结果是 非（⑤中接1的D相或）

4、使用8选1数据选择器实现多输入逻辑函数

1.下边左一：若带圈则接地/输入0；若不带圈则输入1

2.下边中三：一次写三个输入量

3.无视函数中ABC除外的输入，将ABC化成最小项形式

4.将m变成D

5.下边：将上步骤没出现的D引出来接0，前面没乘字母的D引出来接1，前面乘上字母D的D引出来接D，前面乘上字母D非的D引出来接D非，前面乘上字母E的D引出来接E，前面乘上字母E非的D引出来接E非…

6.上边：原式有公共的大非号，那么就在Y非上写L，反之在Y上写L

完整版：

5、使用8选1数据选择器实现L = m格式的3输入逻辑函数

6、使用8选1数据选择器实现L = m格式的4输入逻辑函数

1.下边左一：若带圈则接地/输入0；若不带圈则输入1

2.下边中三：一次写三个输入量

3.将m后的括号展开

4.将m便形成逻辑函数

5.无视函数中ABC以外输入，将ABC化为最小项形式

6.将m变成D

7.下边：将上步骤没出现的D引出来接0，前面没乘字母的D引出来接1，前面乘上字母D的D引出来接D，前面乘上字母D非的D引出来接D非

8.上边：Y输出没带大非号，Y上接L，反之接Y非

如果即接了D又接了D非，可以写成

触发器

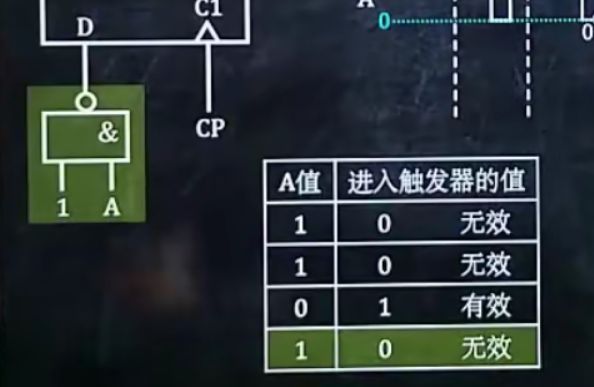
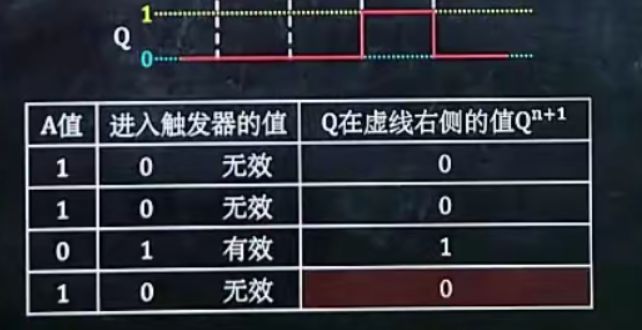
1、给出D触发器及输出，要求画出波形图

1.在CP凸起左侧或右侧向下画虚线：

若C1接口出无“O”，则在左侧

若C1接口处有“O”，则在右侧

2.判断每个虚线处输入变量的值是0还是1（若判断不出，则取稍左偏移的值）

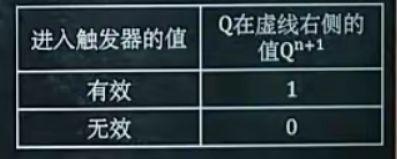
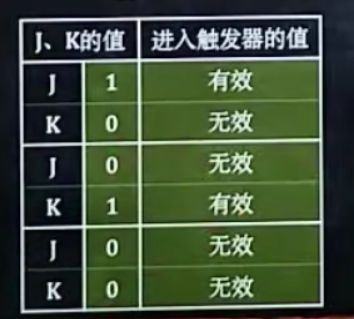
3.判断每个虚线出输入变量的值是有效还是无效。若可使进入触发器的值为1，则有效，反之无效

4.根据下表，得出Q的值，并画在图上

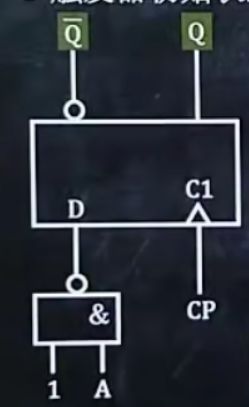
D触发器的特性方程：

Q^n+1 = D

D触发器的样子：

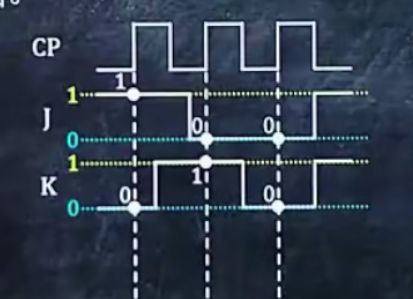
2、给出JK触发器及输入，要求画出波形图

1.在CP凸起左侧或右侧向下画虚线：

若C1接口出无“O”，则在左侧

若C1接口处有“O”，则在右侧

2.判断每个虚线处J、K的值是0还是1（若，判断不出，则取稍微偏左一点）

3.判断每个虚线出J、K的值是有效还是无效，若可以使进入触发器的值为1，则有效，反之无效

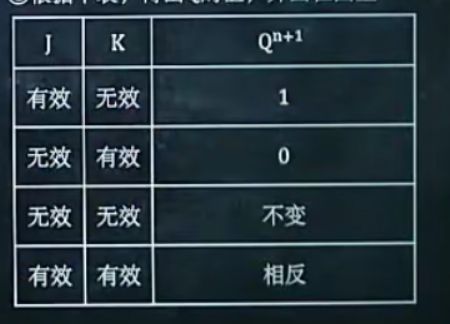
4.根据下表，得出Q的值，并画在图上

J——置位端

K——复位端

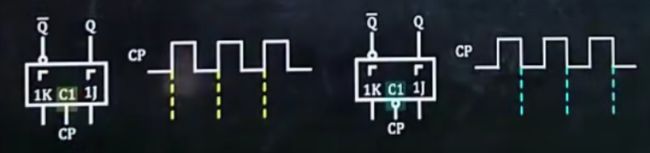
JK触发器特性方程：

JK触发器的逻辑图：

3、多个触发器相连

计数器

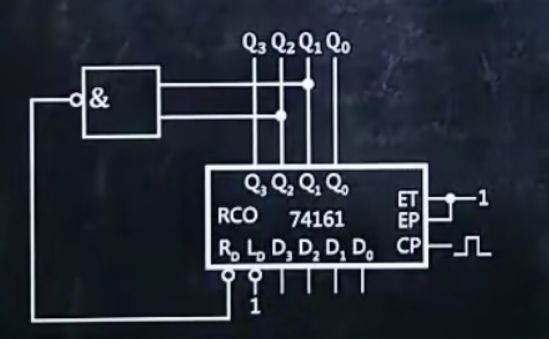
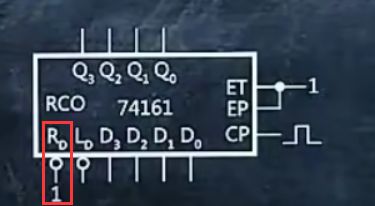
1、使用74161异步清零功能设计N进制计数器

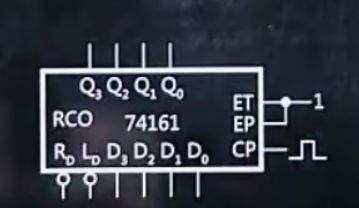
1.画出74161

2.ET、EP连1，CP接凸起

3.在Ld接口处输入1

4.用四位二进制数表示出要求的进制数N

例如 6 = 0110

5.找出N从左到右哪几位数是1，哪几位是1，就在Q3、Q2、Q1、Q0接口对应的位置上接线，接出的线连接一个与非门（多条时）或非门（一条时），再连接到Rd接口上

6.在Q3、Q2、Q1、Q0接口顶部接出来写上Q3、Q2、Q1、Q0

额外例题：设计八进制计数器

N = 8 = 1000

一个1就用非门即可

将Q0、Q1、Q2、Q3接出去

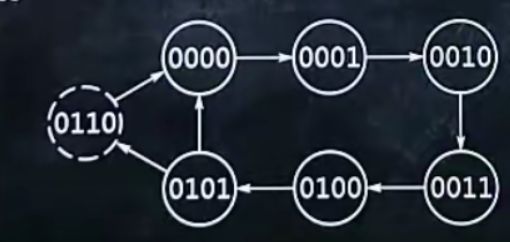
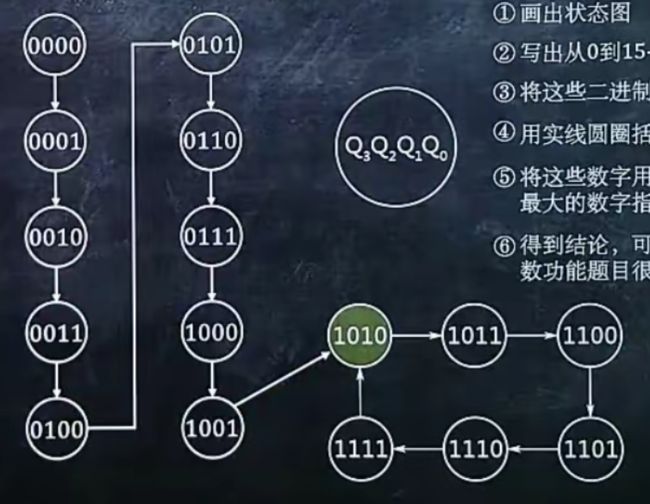
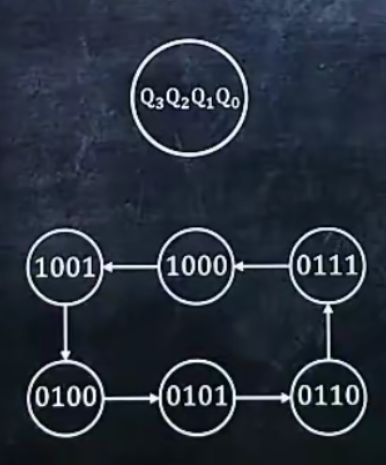
2、使用74161异步清零功能设计N进制计数器后，画出状态图

1.画出

2.写出0到（N - 1）的四位二进制数

3.用实线，在每个二进制数上括个圆圈

4.用“→”从小到大连接所有圆圈，再最后从最大指向最小

5.在0与（N - 1）旁再写上N的四位二进制数

6.用虚线，给N括上个圆圈

7.用“→”，从（N - 1）指向N，再有N指向0

3、用74161异步清零功能设计N进制计数器后，检查自启动

1.画出状态图

2.写出从（N+1）到15的四位二进制数

3.将这些二进制数一次写在状态图上

4.用实线圆圈括住这些数

5.找出N的二进制数再哪些位上是1，若这些数在同样位上也是1，则“→”指向0000，若不是，则“→”指向下一个数

相同指向0000

其他从小到大指向下一个数

6.得到结论，可以自启动（一般都可以自启动）

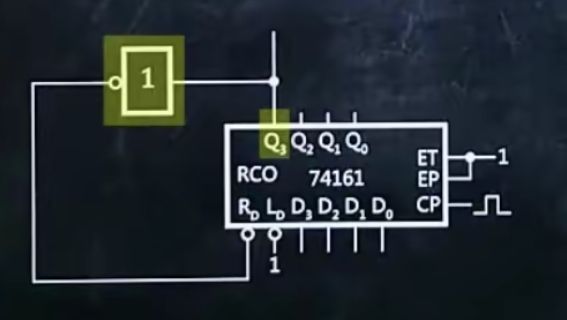
4、使用74161同步置数功能设计N进制计数器

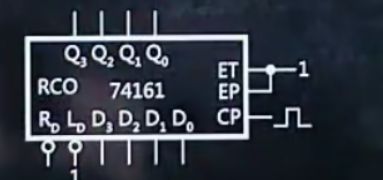
1.画出74161

2.ET、EP接1，CP连凸起

3.给Rd接入1

4.从四位二进制数1111开始依次递减：

5.在RCO上连线非门，再接入Ld

6.再Q3、Q2、Q1、Q0接口顶部写上Q3、Q2、Q1、Q0

5、使用74161同步置数功能设计N进制计数器后，画出状态图

1.画出

2.写出N个四位二进制数

3.用实线，在每个二进制数上括个圆圈

4.用“→”从小到大连接所有圆圈，再从最大指向最小

6、使用74161同步置数功能设计N进制计数器后，检查自启动

1.画出状态图

2.写出从0到（15 - N）的四位二进制数

3.将这些二进制数依次写在状态图上

4.用实现圆圈括住这些数字

5.将这些数字用“→”从小到大连接，最大的数字指向（16 - N）

6.得到结论，可以自启动（很少不能自启动）

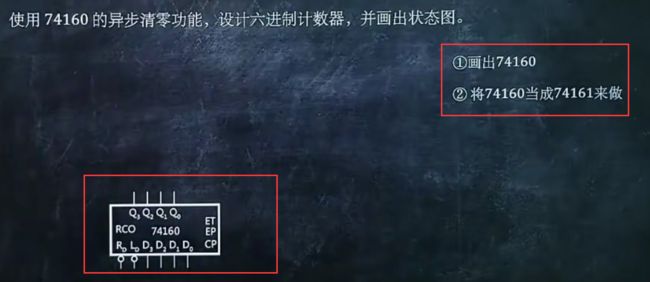
7、使用74160异步清零功能设计N进制计数器，并画状态图

直接把74160当作74161来做，步骤和1、2类型一样

8、使用74160同步置数功能设计N进制计数器

1.画出74160，ET EP连1，CP接凸起

2.给Rd接1

3.从四位二进制数1001开始依次递减：

4.在RCO上连接非门，连接到Ld上

5.在Q3、Q2、Q1、Q0接口顶部写上Q3、Q2、Q1、Q0

9、使用74160同步置数功能设计N进制计数器后，画出状态图

1.画出

2.写出从1001开始N个递减四位二进制

3.用实线，在每个二进制数上括圆圈

4.用“→”从小到大连接所有圆圈，再从最大指向最小

10、使用74161个74151设计某序列发生器

1.根据图像写出循环的八个数

在CP图像上，一高一低的部分作为一个格，高边是1，低边是0

这就是完整的八个数循环

2.画出下图（背下来，画就完事了！）

3.再D0到D7上依次写出循环的八个数

时序电路

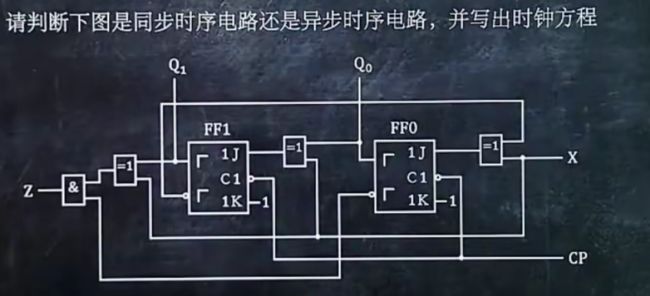
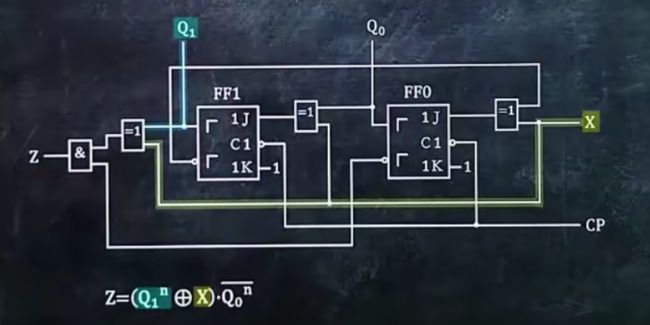
1、判断是同步时序电路还是异步时序电路，并写出时钟方程

判断C1接口是否连在同一个地方，如果连接在同一个地方，那就是同步时序电路，反之是异步时序电路

看C1连出来的是什么，时钟方程就是什么

2、写出时序逻辑电路的输出方程

输出方程就是 Z = …

等号右边由Q1^n、Q0n 等组成

n次方表示当前状态

例题：

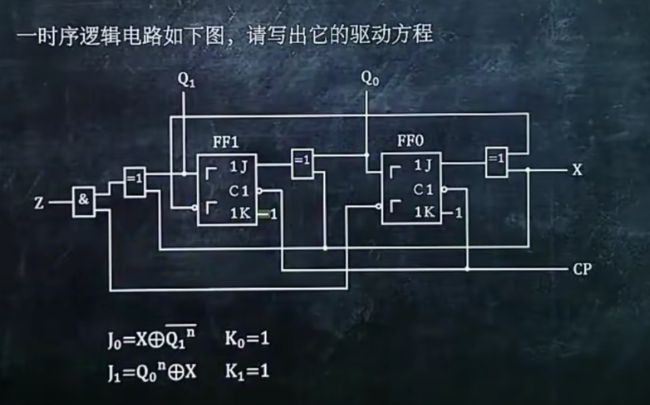
3、写出时序逻辑电路的驱动方程

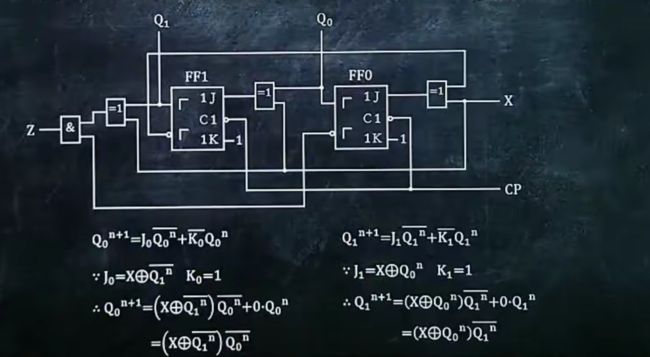
4、写出时序逻辑电路的次态方程

1.写出各个触发器的特性方程

2.将驱动方程得到的J、K或者D带入

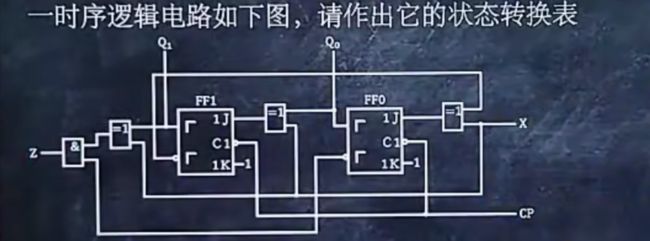
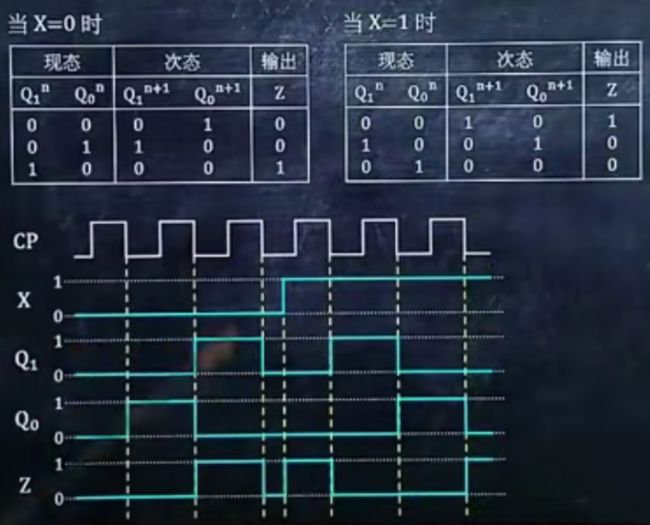
5、作时序逻辑电路的状态转换表

例题：

解题步骤：

1.将输出方程和次态方程算出来

2.分别得出①在未知输入量为0时与为1时的具体方程

3.列出下面两个表格，分别对应未知输入量0与1时，在每个表格里，现态初始为0 0，次态与输出由现态带入②中算得，下一行现态等于上一行次态，直到某行次态为 0 0为止

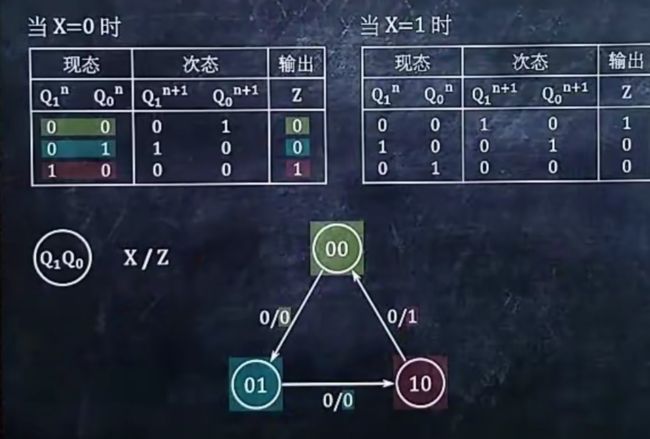
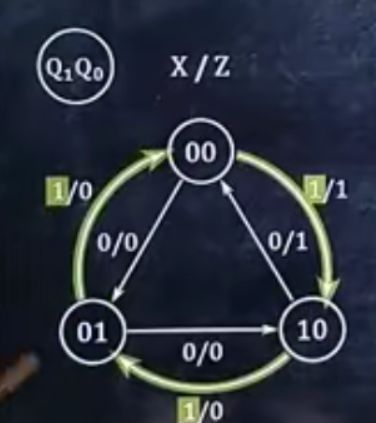
6、作时序逻辑电路的状态图

1.画出

2.旁边写上“位置输入量/Z”

3.将现态的数字写出来并用圆圈圈好

4.按照未知输入量0那个表，在各个圆圈间画→，从表的第一行指向第二行，再从第二行指向第三行…最后从最后一行指向第一行

5.在每个箭头旁边写上“0/发出件头行的Z值”

6.按照未知输入量为1那个表，在各个圆圈间画→，从表的第一行指向第二行，再从第二行指向第三行…最后从最后一行指向第一行

7.在每个箭头旁边写上“1/发出箭头行的Z值”

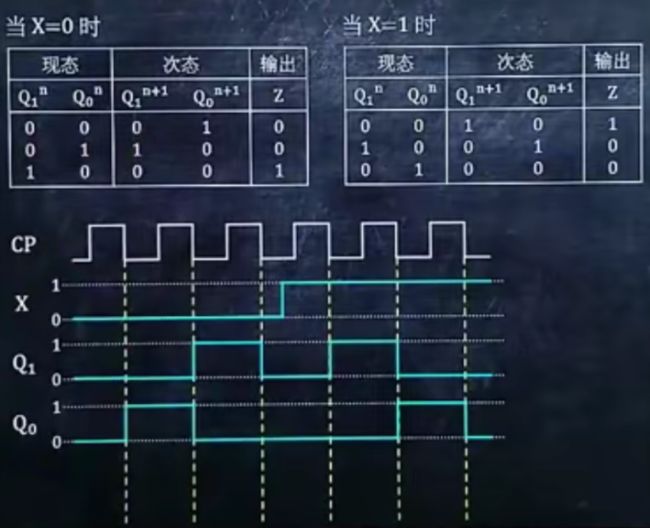
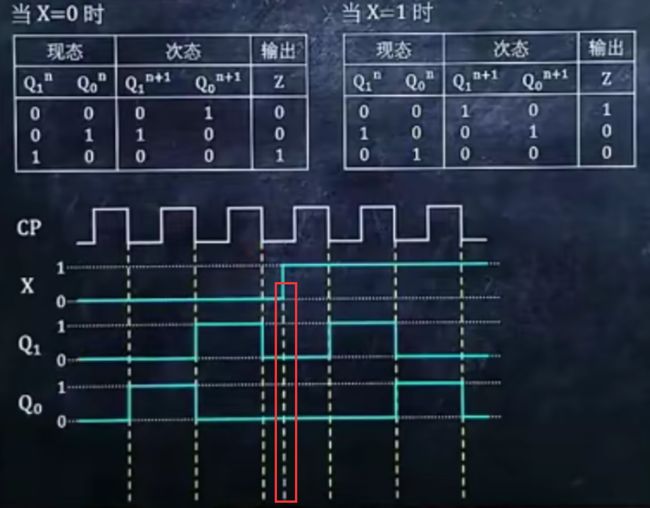
7、作时序逻辑电路的时序图

1.根据状态表找出Q的行数，画（2 × 行数段）凸起的CP图

2.观察原图C1接口出有无圈。有圈，在凸起右侧向下画虚线。若无圈，则在图区左侧向下画虚线

3.在下方画X线，前半段0，后半段1

4.根据状态表将Q0与Q1的图化上

看每一段的最开始状态x是多少

5.在X转折处向下引虚线，根据状态表将Z的图画上

转折处就是从0变1，从1变0的位置

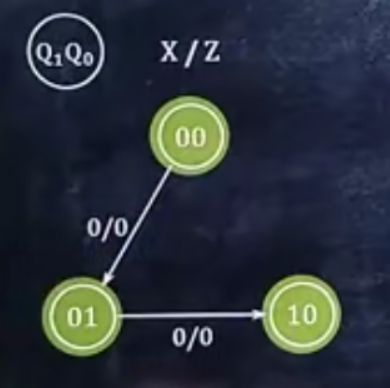
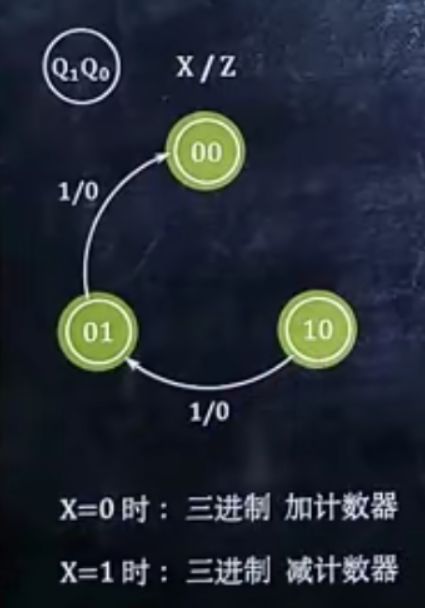
8、分析时序逻辑电路的功能

功能：N进制加计数器/N进制减计数器

先把状态图拿出来

如果x的值不确定

就分情况分析x = 0和x = 1时的功能

总结

如果时序逻辑电路图中的x已知，那么相对简单一点，不需要分情况讨论，只需要把x的确切值带入即可！