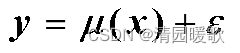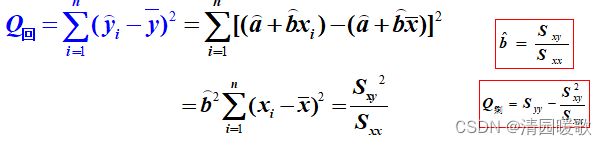回归分析模型

目录

一、回归分析概述

1.1 确定性关系（函数关系）

1.2 非确定性关系（相关关系）

1.3 回归分析

1.4 最小二乘法

二、一元线性回归

三、多元线性回归

四、回归检验

4.1 一元回归检验

4.1.1 方差分析法（F检验法）

4.1.2 相关系数检验（r检验法）

4.1.3 t 检验法

4.2 多元线性回归检验

4.2.1 拟合优度检验（r）——模型有效性

4.2.2 回归方程显著性检验（F）——线性相关性

4.2.3 回归参数显著性检验（t）——各自变量的影响

四、预测与控制

4.1 预测

4.2 控制

五、非线性回归的线性化处理

---

一、回归分析概述

1.1 确定性关系（函数关系）

        确定性关系是指当一些变量的值确定以后另一些变量的值也随之完全确定的关系。

1.2 非确定性关系（相关关系）

        相关关系是指变量之间有一定的依赖关系，但当一些变量的值确定以后，另一些变量的值虽随之变化却并不能完全确定，这时变量间的关系不能精确地用函数来表示。

1.3 回归分析

        回归分析（regression analysis）是数理统计中研究一个响应变量（因变量）与若干个预报变量（自变量）之间相关关系的一种有效方法。可以用一个确定的函数关系式大致地描述y与x的之间的相关关系，称为回归方程。

        只有一个预报变量的回归分析称为一元回归分析；

        多于一个预报变量的回归分析称为多元回归分析。

例如：（1）自变量（预报变量）：父亲身高；因变量（响应变量）：儿子身高

           （2）自变量（预报变量）：IQ，时间T；因变量（响应变量）：成绩

1.4 最小二乘法

 而满足：

称为随机误差，通常假定~N（0，o²）

最小二乘法就是，函数m（x）=m（x，a1，a2，L，ak），其中a1到ak为未知参数，我们选取这些合适的参数，使得观测值yi与相应的函数值的偏差平方和最小

二、一元线性回归

 

三、多元线性回归

        根据最小二乘法，要使得

最小， 对bp求偏导并让他们等于0，其次

 当X'X不可逆或变量之间存在多重共线性关系时，最小二乘法不可用，可采用主成分分析回归等

（X'：转置矩阵；可以对于矩阵A可逆，存在矩阵B使得AB=BA=E，满足一个即可）

四、回归检验

4.1 一元回归检验

4.1.1 方差分析法（F检验法）

Q总：总平方和，反映观测值y1~yn总的分散程度

Q剩：剩余平方和，反映了观测值偏离回归直线的程度，这种偏离是由于观测误差等随机因素引起的

Q回：回归平方和，反映回归值的分散度，这种分散是由于Y与X之间的线性相关关系引起的

Q_回 与Q_剩 的比值反映了这种线性相关关系与随机因素对y的影响，比值约大，线性相关性越强

当H0为真时，

        给定显著性水平α,若F≥F_α,则拒绝假设H_0,即线性关系显著.反之认为y对x没有线性相关关系,所求线性回归方程无实际意义.

4.1.2 相关系数检验（r检验法）

r=S_xy/√(S_xx S_yy )

        若r 的绝对值很小，则y与x线性相关关系不显著，或不存在线性相关关系；若绝对值较大（接近于1）时，才表明线性相关关系显著

（1）若|r|≤r_0.05 (n-2),则认为y与x之间的线性相关关系不显著,或者不存在线性相关关系;

（2）若r_0.05 (n-2)<|r|≤r_0.01 (n-2),则认为y与x之间的线性相关关系显著;

（3）若|r|>r_0.01 (n-2),则认为y与x之间的线性相关关系特别显著.

4.1.3 t 检验法

4.2 多元线性回归检验

4.2.1 拟合优度检验（r）——模型有效性

        构建一个直观判断拟合优劣的指标：R² = SSR / SST

        R²越大，自变量对因变量的解释程度越高，自变量引起的变动占总变动的百分比高。观察点在回归直线附近越密集。 取值范围：0-1

4.2.2 回归方程显著性检验（F）——线性相关性

        检验Y与解释变量x1，x2，……xk之间的线性关系是否显著。

检验的步骤：

（1）提出假设

（2）计算统计量

（3）查表

（4）做检验

4.2.3 回归参数显著性检验（t）——各自变量的影响

        检验是否每个解释变量都对Y显著

（1）提出假设

（2）构造并计算统计量

（3）查表

（4）检验

        |Ti|t_a/2：拒绝

四、预测与控制

4.1 预测

        对于给定的任意x_0，带入到回归方程中

y ̂_0=a ̂+b ̂x_0

        进行区间估计，给定的置信度1-a，求出置信区间，即预测区间

(y ̂_0-σ ̑μ_(α/2),y ̂_0+σ ̑μ_(α/2) )

4.2 控制

        预测的反问题，即观察y在什么范围内，确定x的范围

{(&y_1^′=y ̂_1-σ ̑μ_(α/2)@&y_2^′=y ̂_2+σ ̑μ_(α/2) )

五、非线性回归的线性化处理

采用变量代换法将非线性模型线性化

（1）y = a + bsint    ； 令x = sint

（2）y = a + bt + ct² ；令x_1 = t ，x_2 = t² 化为多元线性回归

（3）令y = 1/y ；x = 1/x

（4）令x = lnx 

可以excel、spss、lingo实现

excel：插入-图表-散点图

        数据-数据分析-回归；设置置信水平95%，a>p则拒绝H_0，R²越接近1，线性相关性越显著，F尽可能大，模型效果越好

spss：散点图

        分析-回归-线性；R和F越大，Sig越小，线性相关关系越显著

        方差分析，如：若F>F_0.5(2,5)=5.2，线性相关关系显著

                                 若F>F_0.01(2,5)=10.2，线性相关关系高度显著

        系数分析：看系数表的 B

画散点图-数据分析-回归-。。。