【二叉树(一)】:二叉树简单实现
二叉树是每个结点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。树是数据结构中的重中之重,尤其以各类二叉树为学习的难点。
1、树的相关概念
1.1、树
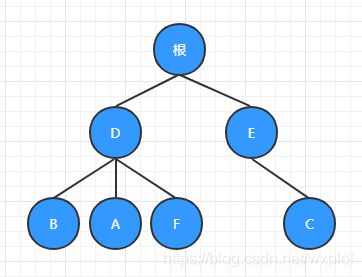
树是一种一对多的数据结构。树又有很多子集,比如:二叉树、二叉搜索树、2-3树、红黑树等等。树的特征:
1.没有父结点的结点叫根,一个树有且只有一个根;
2.每个结点有0个或多个子结点;
3.一颗树里也可拥有子树,且子树不能相交;
树的示例:
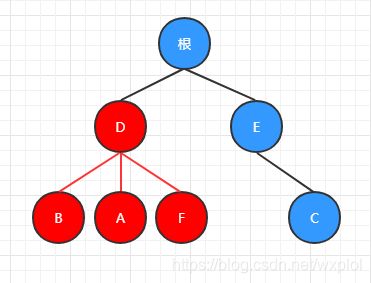
图中标红的为上面这个树的子树:
参考链接:每天一点算法-二叉树 (Day8)
1.2、树的相关术语
树的结点(node):包含一个数据元素及若干指向子树的分支;
孩子结点(child node):结点的子树的根称为该结点的孩子;
双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
祖先结点: 从根到该结点的所经分支上的所有结点
子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙
结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
树的深度:树中最大的结点层
结点的度:结点子树的个数
树的度: 树中最大的结点度。
叶子结点:也叫终端结点,是度为 0 的结点;
分枝结点:度不为0的结点;
有序树:子树有序的树,如:家族树;
无序树:不考虑子树的顺序;
2、二叉树
2.1、二叉树定义
二叉树是n(n>=0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树组成。
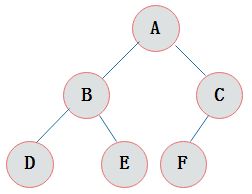
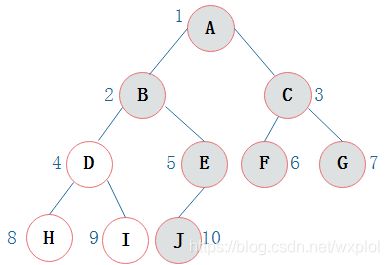
一棵普通二叉树如下所示:
2.2、二叉树的特性
- 一颗二叉树有n个元素(n>0),它有n-1条边
- 一棵二叉树高度为h(h>=0),它至少有h个元素,最多有2^h-1个元素
- 一颗二叉树有n个元素(n>0),它的高度为n,最小高度为[log2(n+1)]
- 完全二叉树的一元素编号为i(1<=i<=n),有以下关系成立
- 如果i=1,该元素为二叉树的根。若i>1,则其父节点的编号为i/2;
- 如果2i>n,则表示该元素无左孩子。否则,其左孩子的编号为2i;
- 如果2i+1>n,则其元素无右孩子。否则其右孩子的编号为2i+1。
2.3、二叉树分类
- 二叉树
二叉树是每个节点最多有两个子树的树结构。
- 满二叉树
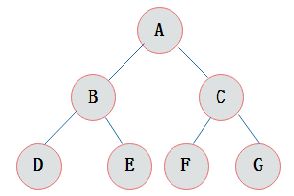
一棵深度为k,且有2^k-1个节点的树是满二叉树。满二叉树如下图:
性质:
1.如果一颗树深度为h,最大层数为k,且深度与最大层数相同,即k=h;
2.它的叶子数是: 2^(h-1)
3.第k层的结点数是: 2^(k-1)
4.总结点数是: 2^k-1 (2的k次方减一)
5.总节点数一定是奇数。
6.树高:h=log2(n+1)。
- 完全二叉树
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h 层所有 的结点都连续集中在最左边,这就是完全二叉树。完全二叉树如下图:
特点:
1)叶子结点只能出现在最下层和次下层。
2)最下层的叶子结点集中在树的左部。
3)倒数第二层若存在叶子结点,一定在右部连续位置。
4)如果结点度为1,则该结点只有左孩子,即没有右子树。
5)同样结点数目的二叉树,完全二叉树深度最小。
注:满二叉树一定是完全二叉树,但反过来不一定成立。
参考链接:深入学习二叉树(一) 二叉树基础
3、二叉树的实现
3.1、数据存储结构
- 顺序存储
二叉树的顺序存储结构就是使用一维数组存储二叉树中的结点,并且结点的存储位置,就是数组的下标索引。
上图所示的一棵完全二叉树采用顺序存储方式,如图下表示:
由上图可以看出,当二叉树为完全二叉树时,结点数刚好填满数组。
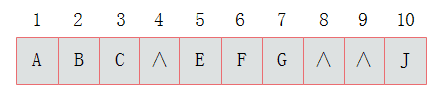
那么当二叉树不为完全二叉树时,采用顺序存储形式如何呢?例如:对于上图描述的二叉树:其中浅色结点表示结点不存在。那么图3.8所示的二叉树的顺序存储结构如图所示:
其中,∧表示数组中此位置没有存储结点。此时可以发现,顺序存储结构中已经出现了空间浪费的情况。
那么对于右斜树极端情况对应的顺序存储结构如图所示:由图可以看出,对于这种右斜树极端情况,采用顺序存储的方式是十分浪费空间的。因此,顺序存储一般适用于完全二叉树。
- 链表存储
既然顺序存储不能满足二叉树的存储需求,那么考虑采用链式存储。由二叉树定义可知,二叉树的每个结点最多有两个孩子。因此,可以将结点数据结构定义为一个数据和两个指针域。
定义结点代码:
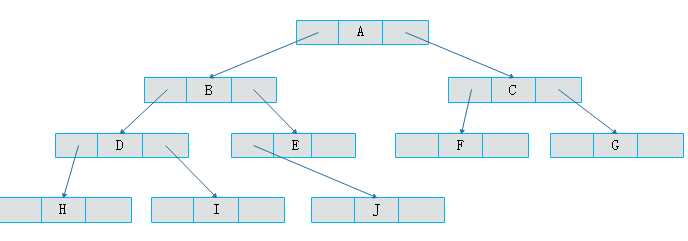
//链表节点 templateclass ListNode { public: ListNode():value_(NULL),front(nullptr),next(nullptr){} ListNode(const T &value):value_(value),front(nullptr),next(nullptr){} ListNode(const T &value, ListNode *left, ListNode *right): value_(value), front(left), next(right){} ListNode(const ListNode &theNode): value_(theNode.value_), front(nullptr), next(nullptr){} public: T value_; ListNode *front; ListNode *next; }; 二叉树可以采用下表示。
图中采用一种链表结构存储二叉树,这种链表称为二叉链表。
作者:MrHorse1992
链接:https://www.jianshu.com/p/bf73c8d50dc2
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2、二叉树遍历
二叉树的根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次,且仅被访问一次。
二叉树的访问次序可以分为四种:前序遍历、中序遍历、后序遍历和层序遍历。
- 前序遍历
前序遍历通俗的说就是从二叉树的根结点出发,当第一次到达结点时就输出结点数据,按照先向左在向右的方向访问。
二叉树前序遍历如下:
1)从根结点出发,则第一次到达结点A,故输出A;
2)继续向左访问,第一次访问结点B,故输出B;
3)按照同样规则,输出D,输出H;
4)当到达叶子结点H,返回到D,此时已经是第二次到达D,故不在输出D,进而向D右子树访问,D右子树不为空,则访问至I,第一次到达I,则输出I;
5)I为叶子结点,则返回到D,D左右子树已经访问完毕,则返回到B,进而到B右子树,第一次到达E,故输出E;
6)向E左子树,故输出J;
7)按照同样的访问规则,继续输出C、F、G;二叉树的前序遍历输出为:A->B->D->H->I->E->J->C->F->G。
- 中序遍历
中序遍历就是从二叉树的根结点出发,当第二次到达结点时就输出结点数据,按照先向左在向右的方向访问。
二叉树中序遍历如下:
1)从根结点出发,则第一次到达结点A,不输出A,继续向左访问,第一次访问结点B,不输出B;继续到达D,H;
2)到达H,H左子树为空,则返回到H,此时第二次访问H,故输出H;
3)H右子树为空,则返回至D,此时第二次到达D,故输出D;
4)由D返回至B,第二次到达B,故输出B;
5)按照同样规则继续访问,输出J、E、A、F、C、G。二叉树的中序遍历输出为:H->D->I->B->J->E->A->F->C->G。
- 后序遍历
后序遍历就是从二叉树的根结点出发,当第三次到达结点时就输出结点数据,按照先向左在向右的方向访问。
二叉树后序遍历如下:
1)从根结点出发,则第一次到达结点A,不输出A,继续向左访问,第一次访问结点B,不输出B;继续到达D,H;
2)到达H,H左子树为空,则返回到H,此时第二次访问H,不输出H;
3)H右子树为空,则返回至H,此时第三次到达H,故输出H;
4)由H返回至D,第二次到达D,不输出D;
5)继续访问至I,I左右子树均为空,故第三次访问I时,输出I;
6)返回至D,此时第三次到达D,故输出D;
7)按照同样规则继续访问,输出J、E、B、F、G、C,A;二叉树的中序遍历输出为:H->I->D->J->E->B->F->G->C->A。
作者:MrHorse1992
链接:https://www.jianshu.com/p/bf73c8d50dc2
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
- 层序遍历
层次遍历就是按照树的层次自上而下的遍历二叉树。
二叉树层序遍历如下:
1)把根节点A放入队列,此时队列为:A,队列头指针指向A,也就是队列第一个元素
2、把当前队列头指针所指元素的左右儿子放入队列,即将B C放入队列,此时队列为A B C ,队列头指针向下移一格,此时指向B
3、不断重复2步骤。此时把B的左右儿子取出来放入队尾,队列变为A B C D E,队列头指针后移,指向C,把C的左右儿子取出来放入队尾,队列变为A B C D E F G;
4、依次类推,直到队列头指针和为指针重合时,输出最后一个元素,算法结束。队列从头到尾输出一遍,就是按层遍历,这个队列是动态的,只要有子节点,子节点就会不停的加入队尾,但总有子节点没有的时候,所以,队列尾指针肯定有不再移动的时候,而头指针一直在一步一步向下移,总会有首尾指针重合的时候,即标志着算法结束。
二叉树的层次遍历结果为:A->B->C->D->E->F->G->H->I->J。
参考链接:二叉树的按层遍历法
3.3、二叉树的算法实现
template
class BTree
{
public:
virtual ~BTree(){}
virtual bool empty() const =0;
virtual size_t size() const=0;
//前序遍历
virtual void preOrder()=0;
//中序遍历
virtual void inOrder()=0;
//后序遍历
virtual void postOrder()=0;
//层次遍历
virtual void levelOrder()=0;
}; /*******************************************
* 二叉树的数组实现 *
/*******************************************/
template
class ArrayBTree
{
public:
ArrayBTree(const size_t &capacity=10);
~ArrayBTree(){}
//二叉树元素的数量
size_t size() const{return size_;}
//二叉树的容量
size_t max_size() const{return capacity_;}
//二叉树是否为空
bool empty() const{return size_==0;};
//向二叉树中插入元素
void insert(const T &value);
//删除二叉树中的元素
void erase(const T &value);
//修改二叉树中的元素
void set(const T &index,const T &value);
//查找二叉树中的元素
T get(const int &index);
//二叉树中搜索对应值位置的下标
int find(const T &value);
//打印二叉树
void print();
//前序遍历
void preOrder();
//中序遍历
void inOrder();
//后序遍历
void postOrder();
//层次遍历
void levelOrder();
private:
void insert_(const T &value,int index); //插入元素
void erase_(const int &index); //删除元素并重新调整二叉树
int find_(const T &value,int index); //搜索二叉树
void preOrder_(const int &index); //前序遍历
void inOrder_(const int &index); //中序遍历
void postOrder_(const int &index); //后序遍历
void levelOrder_(const int &index); //层次遍历
private:
shared_ptr ptr_; //存储二叉树数的数组
size_t size_; //二叉树元素的大小
size_t capacity_; //二叉树的容量
};
template
ArrayBTree::ArrayBTree(const size_t &capacity):capacity_(capacity),
size_(0)
{
ptr_=shared_ptr(new T[capacity_],[](T *p){delete[] p;});
fill(ptr_.get(),ptr_.get()+capacity_,-1);
}
template
void ArrayBTree::insert_(const T &value, int index)
{
if(index>=capacity_){
cerr<<"index out of capacity(in function insert_)"<=value){
insert_(value,index*2+1);
}else{
insert_(value,index*2+2);
}
}
}
template
void ArrayBTree::insert(const T &value)
{
if(size_+1>=capacity_){
cerr<<"tree capacity is out of max size"<empty()){
*ptr_.get()=value;
}else{
insert_(value,0);
}
++size_;
}
template
void ArrayBTree::erase_(const int &index)
{
if(index*2+1>=capacity_ || (ptr_.get()[index*2+1]==-1 &&
ptr_.get()[index*2+2]==-1)){
ptr_.get()[index]=-1;
return ;
}
if(ptr_.get()[index*2+1]!=-1 && (ptr_.get()[index*2+2]==-1 ||
ptr_.get()[index*2+2]>=capacity_)){
ptr_.get()[index]=-1;
T value=ptr_.get()[index*2+1];
ptr_.get()[index*2+1]=-1;
insert(value);
return ;
}
ptr_.get()[index]=ptr_.get()[index*2+2];
erase_(index*2+2);
}
template
void ArrayBTree::erase(const T &value)
{
int index=find(value);
if(-1==index){
cerr<<"erase id fail,"<
void ArrayBTree::set(const T &index, const T &value)
{
if(index<0 || index>=capacity_){
cerr<<"index out of capacity(in function insert_)"<
T ArrayBTree::get(const int &index)
{
if(index<0 || index>=capacity_){
cerr<<"index out of capacity(in function insert_)"<
int ArrayBTree::find_(const T &value, int index)
{
if(ptr_.get()[index]==-1 || index>=capacity_){
cerr<<"Don't find "< value){
return find_(value,index*2+1);
} else{
return find_(value,index*2+2);
}
}
template
int ArrayBTree::find(const T &value)
{
if(this->empty()){
cerr<<"tree is empty"<
void ArrayBTree::print()
{
for(auto i=0;i
void ArrayBTree::preOrder_(const int &index)
{
if(index>=capacity_ || ptr_.get()[index]==-1){
return;
}
cout<
void ArrayBTree::preOrder()
{
preOrder_(0);
}
template
void ArrayBTree::inOrder_(const int &index)
{
if(index>=capacity_ || ptr_.get()[index]==-1){
return;
}
inOrder_(index*2+1);
cout<
void ArrayBTree::inOrder()
{
inOrder_(0);
}
template
void ArrayBTree::postOrder_(const int &index)
{
if(index>=capacity_ || ptr_.get()[index]==-1){
return;
}
postOrder_(index*2+1);
postOrder_(index*2+2);
cout<
void ArrayBTree::postOrder()
{
postOrder_(0);
}
template
void ArrayBTree::levelOrder_(const int &index)
{
if(index>=capacity_ || ptr_.get()[index]==-1){
return;
}
int left=0,right=0;
left=right=index;
while(left
void ArrayBTree::levelOrder()
{
levelOrder_(0);
} /*******************************************
* 二叉树的链表实现 *
/*******************************************/
template
class ListBTree:public BTree
{
public:
ListBTree():phead_(nullptr),size_(0){}
ListBTree(const ListBTree &other); //拷贝构造函数,复制整棵树
~ListBTree();
//获取二叉树的根
ListNode *get_root(){return phead_;}
//判断二叉树是否为空
bool empty() const{return size_==0;}
//返回二叉树元素的个数
size_t size() const{return size_;}
size_t &set_size(){return size_;}
//插入节点
void insert(const T &value);
void insert(const ListNode &theNode);
//删除节点
void erase(const T &value);
//二叉树中搜索对应值位置
ListNode *find(const T &value);
//拷贝二叉树
ListNode *clone() const;
//前序遍历
void preOrder();
//中序遍历
void inOrder();
//后序遍历
void postOrder();
//层次遍历
void levelOrder();
private:
void insert_(ListNode *node,ListNode *&cur); //插入节点
void erase_(const T &value,ListNode *&node); //删除节点
void delete_(ListNode *node); //删除整个二叉树
ListNode *clone_(ListNode *node) const; //拷贝二叉树
void preOrder_(ListNode *node); //前序遍历
void inOrder_(ListNode *node); //中序遍历
void postOrder_(ListNode *node); //后序遍历
ListNode *get_parents(ListNode *node); //获取当前节点的父节点
private:
ListNode *phead_;
size_t size_;
};
template
ListBTree::ListBTree(const ListBTree &other)
{
if(other.empty()){
phead_= nullptr;
}else{
phead_=other.clone();
}
}
template
void ListBTree::delete_(ListNode *node)
{
if(node!= nullptr){
ListNode *cur=node;
delete_(node->front);
delete_(node->next);
delete cur;
cur= nullptr;
}
}
template
ListBTree::~ListBTree()
{
if(phead_!= nullptr){
delete_(phead_);
}
}
template
void ListBTree::insert_(ListNode *node,ListNode *&cur)
{
if(cur== nullptr) {
cur = new ListNode(node->value_);
return ;
}
if(cur->value_<=node->value_){
insert_(node,cur->next);
} else{
insert_(node,cur->front);
}
}
template
void ListBTree::insert(const T &value)
{
ListNode *node=new ListNode(value);
if(phead_== nullptr){
phead_=node;
}else{
insert_(node,phead_);
}
++size_;
}
template
void ListBTree::insert(const ListNode &theNode)
{
ListNode *node=new ListNode(theNode);
if(phead_== nullptr){
phead_=node;
}else{
insert_(node,phead_);
}
++size_;
}
template
void ListBTree::erase_(const T &value, ListNode *&node)
{
if(node== nullptr){
return ;
}
if(valuevalue_){
erase_(value,node->front);
} else if(value>node->value_){
erase_(value,node->next);
}else if(node->front!= nullptr && node->next!= nullptr){
ListNode *tmp=node->next;
while(tmp->front!= nullptr){
tmp=tmp->front;
}
node->value_=tmp->value_;
erase_(node->value_,node->next);
}else{
ListNode *tmp=node;
node=(node->front!= nullptr)?node->front:node->next;
delete tmp;
tmp= nullptr;
}
}
template
void ListBTree::erase(const T &value)
{
if(phead_== nullptr){
return ;
}
erase_(value,phead_);
--size_;
}
template
ListNode *ListBTree::find(const T &value)
{
if(phead_== nullptr){
return nullptr;
}
ListNode *cur=phead_;
while(cur != nullptr){
if(cur->value_next;
} else if(cur->value_>value){
cur=cur->front;
}else{
return cur;
}
}
return nullptr;
}
template
ListNode *ListBTree::clone_(ListNode *node) const
{
if(node== nullptr){
return nullptr;
}
return new ListNode(node->value_,
clone_(node->front),
clone_(node->next));
}
template
ListNode *ListBTree::clone() const
{
if(phead_== nullptr){
return nullptr;
}
return clone_(phead_);
}
template
void ListBTree::preOrder_(ListNode *node)
{
if(node== nullptr){
return ;
}
cout<value_<<" ";
preOrder_(node->front);
preOrder_(node->next);
}
template
void ListBTree::preOrder()
{
if(phead_== nullptr){
return ;
}
preOrder_(phead_);
}
template
void ListBTree::inOrder_(ListNode *node)
{
if(node== nullptr){
return ;
}
inOrder_(node->front);
cout<value_<<" ";
inOrder_(node->next);
}
template
void ListBTree::inOrder()
{
if(phead_== nullptr){
return ;
}
inOrder_(phead_);
}
template
void ListBTree::postOrder_(ListNode *node)
{
if(node== nullptr){
return ;
}
postOrder_(node->front);
postOrder_(node->next);
cout<value_<<" ";
}
template
void ListBTree::postOrder()
{
if(phead_== nullptr){
return ;
}
postOrder_(phead_);
}
template
void ListBTree::levelOrder()
{
if(phead_== nullptr){
return ;
}
ListQueue* > queue;
queue.push(phead_);
while(!queue.empty()){
ListNode *cur=queue.pop();
cout<value_<<" ";
if(cur->front!= nullptr){
queue.push(cur->front);
}
if(cur->next!= nullptr){
queue.push(cur->next);
}
}
} 详细代码可以参考我的github代码:https://github.com/kingqiuol/algorithm_practice/blob/master/assignment5/binary_tree.h