一起刷算法与数据结构-树篇1

大家好，我是工藤学编程	大二在读
作业侠系列最新文章	Java实现聊天程序
一起备战ccf-csp与蓝桥杯系列最新文章	一起备战蓝桥杯与CCF-CSP之大模拟炉石传说
一起刷算法与数据结构最新文章	一起刷算法与数据结构-树篇1

之前我们的链表篇已经完结:
一起刷算法与数据结构-链表篇1
一起刷算法与数据结构-链表篇2

---

说明:

在此栏中，我不生产题解，但我是题解的搬运工，写此栏主要用于自己后续的复习
今天这篇内容如下:

---

今天咱们的内容如下:

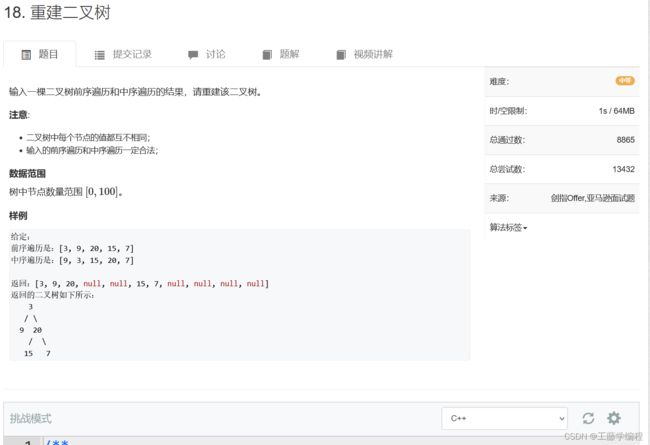
题目1.重建二叉树
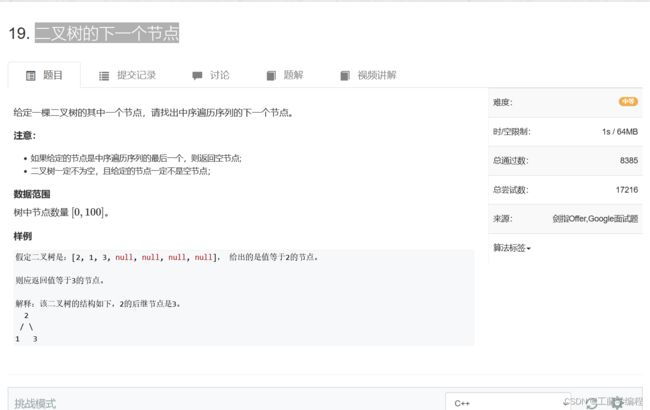
题目2.二叉树的下一个节点
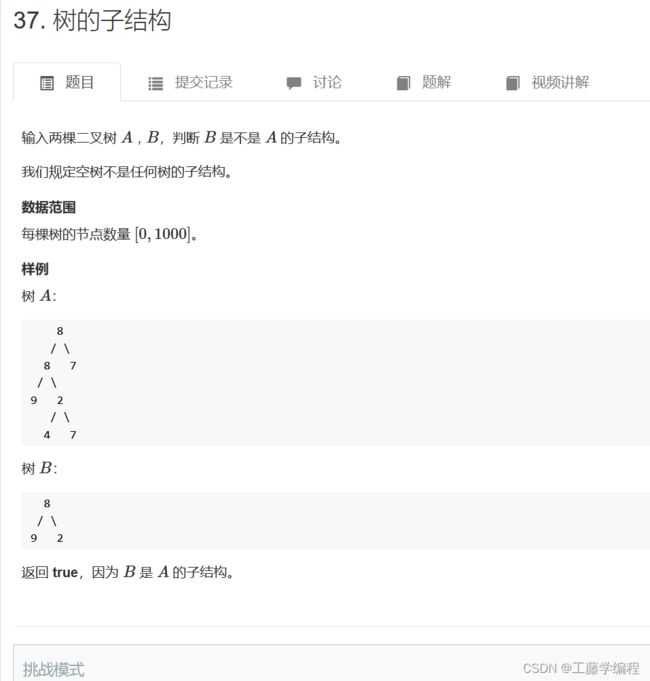
题目3.树的子结构
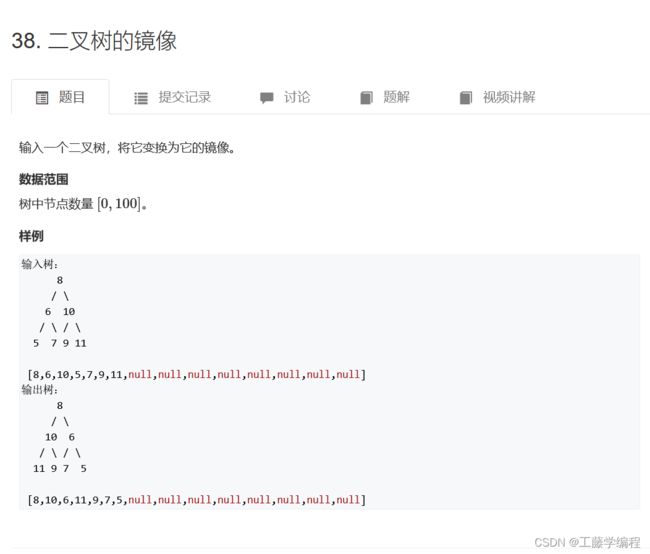
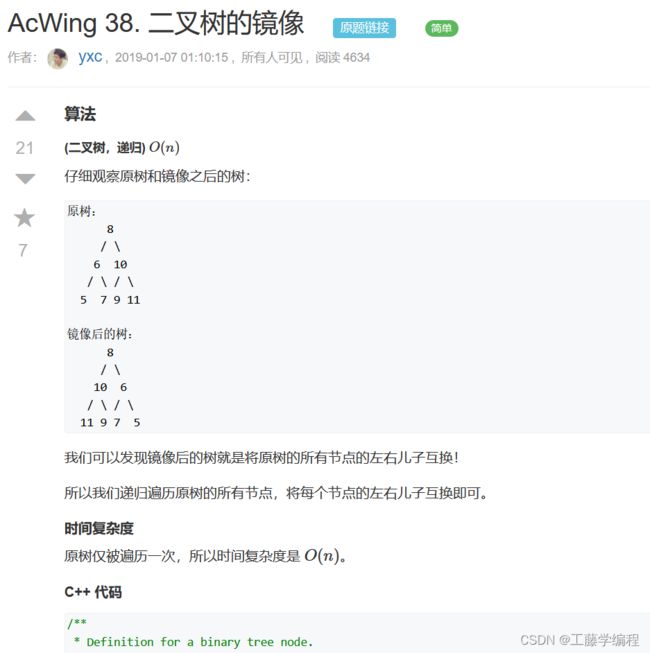
题目4.二叉树的镜像
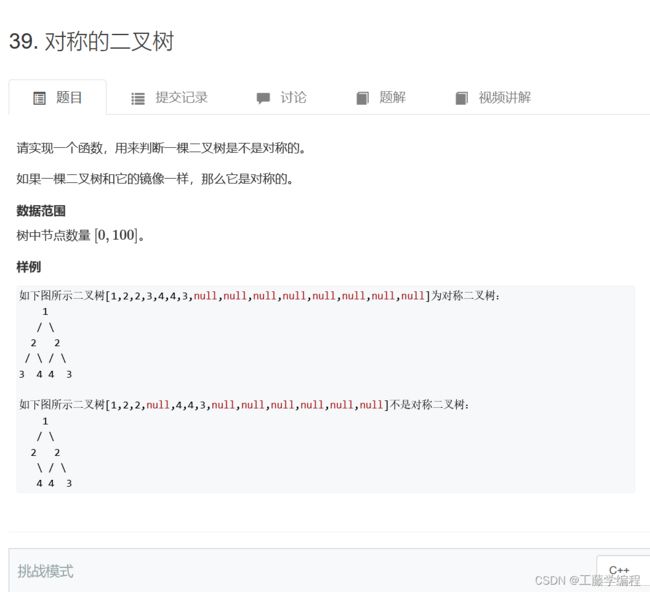
题目5.对称的二叉树
题目6.不分行从上往下打印二叉树
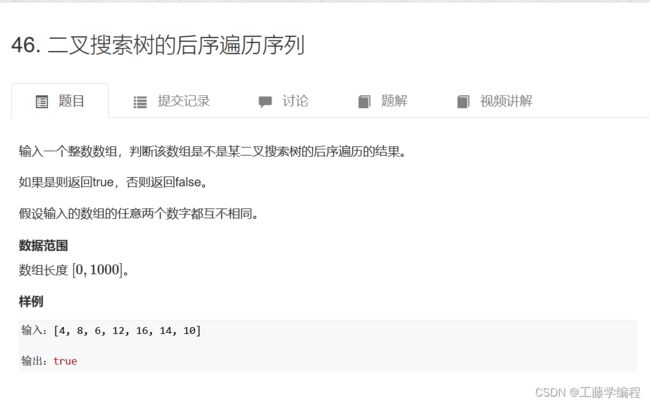
题目7.二叉搜索树的后续遍历序列
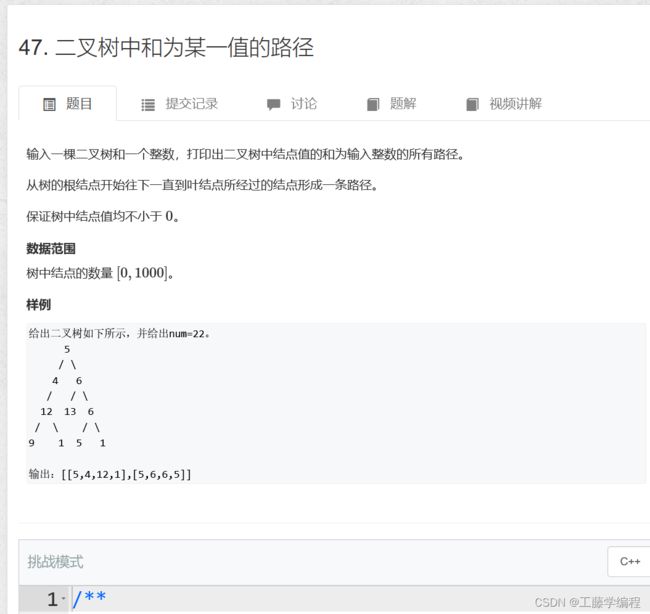
题目8:二叉树中和为某一值的路径
题目9.二叉搜索树的第K个节点
题目10.二叉树的深度

题目1.重建二叉树

解决思路:
看y总：
参考代码:

class Solution {
public:
    unordered_map<int,int>pos;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
         for(int i=0;i<n;i++) pos[inorder[i]]=i;
         return dfs(preorder,inorder,0,n-1,0,n-1);
         
    }
    TreeNode* dfs(vector<int>& pre, vector<int>& in,int pl,int pr,int il,int ir)
    {
        if(pl>pr) return NULL;
        int k = pos[pre[pl]]-il;
        auto root = new TreeNode(pre[pl]);
        root->left=dfs(pre,in,pl+1,pl+k,il,il+k-1);
        root->right=dfs(pre,in,pl+k+1,pr,il+k+1,ir);
        return root;
    }
};

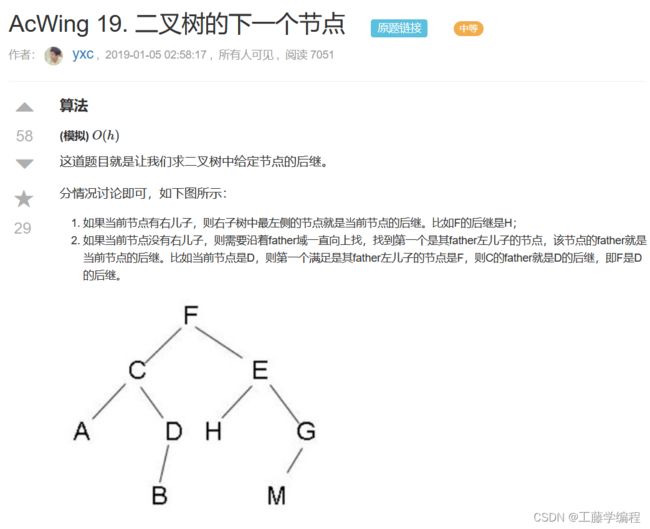
题目2.二叉树的下一个节点

解题思路：
继续看y总：

参考代码:

class Solution {
public:
    TreeNode* inorderSuccessor(TreeNode* p) {
        
        if(p->right)
        {
            p=p->right;
            while(p->left) p = p->left;
            return p;
        }
        while(p->father && p==p->father->right) p=p->father;
        return p->father;
        
    }
};

题目3.树的子结构

y总yyds
参考代码:

class Solution {
public:
    bool hasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
        if(!pRoot1 || !pRoot2) return false;
        if(ispart(pRoot1,pRoot2)) return true;
        return hasSubtree(pRoot1->left,pRoot2) || hasSubtree(pRoot1->right,pRoot2);
    }
    bool ispart(TreeNode* p1,TreeNode* p2)
    {
        if(!p2) return true;
        if(!p1) return false;
        if(p1->val == p2->val) return ispart(p1->left,p2->left) && ispart(p1->right,p2->right);
        return false;
    }
};

题目4.二叉树的镜像

题解:

参考代码

class Solution {
public:
    void mirror(TreeNode* root) {
        if(!root) return;
        mirror(root->right);
        mirror(root->left);
        swap(root->left,root->right);
    }
};

题目5.对称的二叉树
解题思路:

两个子树互为镜像当且仅当：
两个子树的根节点值相等；
第一棵子树的左子树和第二棵子树的右子树互为镜像，且第一棵子树的右子树和第二棵子树的左子树互为镜像；

参考代码：

class Solution {
public:
    bool isSymmetric(TreeNode* root) {
        if(!root) return true;
        return dfs(root->left,root->right);
    }
    bool dfs(TreeNode* l,TreeNode* r)
    {
        if(!l || !r) return !l && !r;
        if(l->val != r->val ) return false;
        return dfs(l->left,r->right) && dfs(l->right,r->left);
    }
    
};

题目6.不分行从上往下打印二叉树

解题思路:

我们从根节点开始按宽度优先的顺序遍历整棵树，每次先扩展左儿子，再扩展右儿子。
这样我们会：
先扩展根节点；
再依次扩展根节点的左右儿子，也就是从左到右扩展第二层节点；
再依次从左到右扩展第三层节点；
依次类推
所以BFS的顺序就是这道题目要求的顺序。
也就是树的层序遍历

参考代码:

class Solution {
public:

    vector<int> printFromTopToBottom(TreeNode* root) {
       vector<int>ans;
       if(!root) return ans;
       queue<TreeNode*>q;
       q.push(root);
       while(!q.empty())
       {
           auto t = q.front();
           q.pop();
           ans.push_back(t->val);
           if(t->left) q.push(t->left);
           if(t->right) q.push(t->right);
       }
       return ans;
    }
};

题目7.二叉搜索树的后续遍历序列

前置知识:

什么是二叉搜索树:
它或者是一棵空树，或者是具有下列性质的二叉树：
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； 它的左、右子树也分别为二叉排序树。

解题思路:

根据其性质，递归判断是否符合即可
参考代码:

class Solution {
public:
vector<int>se;
    bool verifySequenceOfBST(vector<int> sequence) {
        se=sequence;
        return dfs(0,se.size()-1);
    }
    bool dfs(int l,int r)
    {
        if(l>=r) return true;
        int root=se[r];
        int k=l;
        while(k<r && se[k]<root) k++;
        for(int i=k;i<r;i++)
        if(se[i]<root) return false;
        return dfs(l,k-1) && dfs(k,r-1);
    }
};

题目8:二叉树中和为某一值的路径

解题思路:

递归直到树的叶子节点，如果sum等于0，则说明是符合要求

参考代码:

class Solution {
public:
    vector<vector<int>>ans;
    vector<int>cur;
    vector<vector<int>> findPath(TreeNode* root, int sum) {
        dfs(root,sum);
        return ans;
    }
    void dfs(TreeNode* root,int sum)
    {
        if(!root) return;
        cur.push_back(root->val);
        sum-=root->val;
        if(!sum && !root->left && !root->right ) ans.push_back(cur);
        dfs(root->left,sum);
        dfs(root->right,sum);
        cur.pop_back();
    }
};

题目9.二叉搜索树的第K个节点

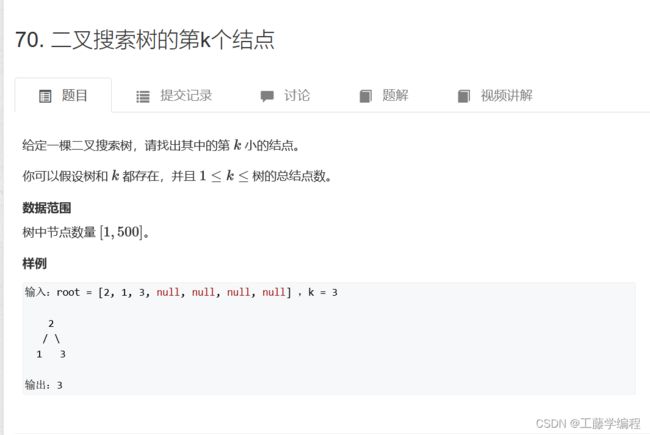
参考大佬题解:
第k大k小问题

参考代码:

class Solution {
public:
TreeNode* ans;
    TreeNode* kthNode(TreeNode* root, int k) {
        dfs(root,k);
        return ans;
    }
    // TreeNode* dfs(TreeNode* root,int& k)
    // {
    //     if(!root) return NULL;
    //     dfs(root->left,k);
    //     k--;
    //     if(k==0)
    //     {
    //         ans=root;
    //     }
    //     if(k>0) dfs(root->right,k);
    // }
    void dfs(TreeNode* root,int& k)
    {
        if(!root) return ;
        dfs(root->left,k);
        k--;
        if(k==0)
        {
            ans=root;
        }
        if(k>0) dfs(root->right,k);
    }
};

注意，如果是这样写是不正确的:

class Solution {
public:
    TreeNode* kthNode(TreeNode* root, int k) {
        return dfs(root,k);
    }
    TreeNode* dfs(TreeNode* root,int& k)
    {
        if(!root) return NULL;
        dfs(root->left,k);
        k--;
        if(k==0)
        {
            return root;
        }
        dfs(root->right,k);
    }
};

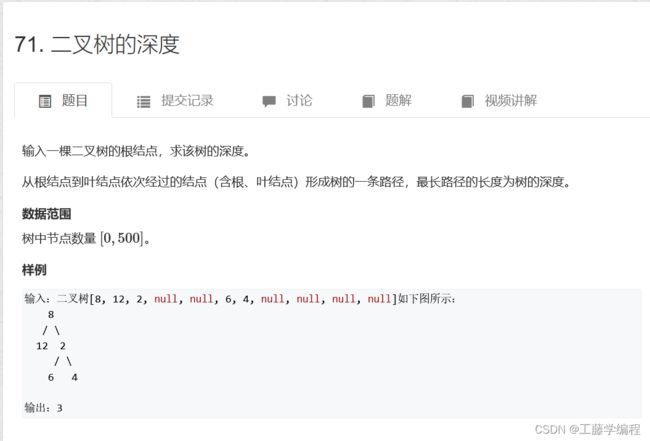
题目10.二叉树的深度

解题思路：

递归遍历，找到最长的即可

参考代码:

class Solution {
public:
int mmax;
    int treeDepth(TreeNode* root) {
        dfs(root,1);
        return mmax;
    }
    void dfs(TreeNode* root,int k)
    {
        if(!root) return;
        if(root->left) dfs(root->left,k+1);
       if(root->right) dfs(root->right,k+1);
        if(k>mmax) mmax=k;
        
    }
};