基于标签量信息的联邦学习节点选择算法

摘要

针对节点数据分布差异给联邦学习算法性能带来不良影响的问题，提出了一个基于标签量信息的节点选择算法。算法设计了一个关于节点标签量信息的优化目标，考虑在一定时耗限制下选择标签分布尽可能均衡的节点组合优化问题。根据节点组合的综合标签分布与模型收敛的相关性，新算法降低了全局模型的权重偏移上界以改善算法的收敛稳定性。仿真验证了新算法与现有的节点选择算法相比拥有更高的收敛效率。

关键词： 联邦学习 ; 节点选择 ; 通信时延

1 引言

目前，机器学习已被广泛应用于科学研究中，而日益受人们关注的信息安全问题让人们意识到传统机器学习技术在处理敏感数据时无法有效保护数据隐私的局限性。为此一项名为联邦学习（federated learning）的新兴机器学习技术于2016年由谷歌公司提出。联邦学习假设训练数据由节点产生并存储在本地，与服务器的通信内容为节点训练求得的模型参数而非数据本身，因此避免了用户数据在传输过程中的隐私泄露问题，更适用于处理大规模敏感数据。而联邦学习主要有两个要解决的问题：一是无线网络下实现多轮迭代训练的通信难题，在带宽资源有限与节点数量庞大的场景中实现迭代通信对通信效率有着高要求；二是联邦学习中全局模型的收敛难题，节点数据由本地产生且不互通，分布上存在的差异导致节点训练出的模型参数收敛方向不一致，进而对全局模型的收敛造成不良影响。

节点选择作为有效降低通信量的手段，是联邦学习中不可或缺的环节，如最初被提出的联邦学习算法FedAvg（federated averaging）[1]采取了随机选择策略，服务器每回合以相等概率随机选择出一定比例的节点参与训练。之后人们在节点选择环节引入了许多能反映节点间各项差异的指示信息，用更复杂的节点选择算法来进一步提升联邦学习算法的各项性能，包括节点通信条件[2,3,4,5,6,7]、模型梯度信息[4,8,9,10,11,12]等。根据节点通信条件，服务器可通过舍弃通信条件差或训练耗时较长的节点提高整体通信效率，如文献[2]提出了一种优先选择信道条件好、信噪比高的节点的选择方法，文献[3]与之类似地提出了优先选择耗时较短的节点的贪心选择算法。文献[5]在考虑降低平均通信时间的同时还考虑了长期公平（long-term fairness）的问题，能让节点的被选频率分布更加均匀。而模型梯度信息能反映节点更新样本的方向差异，因此服务器可优先选取质量较优的节点更新样本提高全局模型的收敛效率等，如文献[8]借助一个能代表全局方向的辅助数据集，训练获得参照更新方向后，优先选取偏离程度较低的节点样本进行全局模型的更新。文献[9]设计了一种阈值法，所有节点在训练完成后向服务器提供其相对于训练前的模型范数等信息，计算出阈值后选择满足阈值条件的节点参与训练。此外，也有同时利用通信条件与模型质量的方法，如文献[4]提出了一种概率选择的方案，各节点的被选概率由其所处信道容量以及模型质量综合决定。

本文提出了使用标签量信息作为指示信息来设计节点选择方法的新思路，其在能反映节点数据分布差异的同时，相较于模型参数信息有着计算简单、可在训练前获取、兼容性高等优势。具体而言，本文基于标签量信息介绍了一个名为GEMD（group earth-mover’s distance）的参量，该参量能反映节点组合的综合标签分布相对于全局分布的差异。本文还提出了 GEMD 与联邦学习全局模型的收敛偏移上界之间的相关性。基于 GEMD 本文设计了考虑通信时间限制的类背包节点选择算法FedBag，优化目标为选择在一定通信时耗限制内的标签分布最均衡的节点组合作为输出，旨在改善节点组合的综合标签分布的同时控制每回合的通信时耗，从而减轻节点数据分布对模型收敛稳定性的负面影响。最后，通过与随机策略以及现有节点选择算法FedCS[3]的仿真对照，验证了所提算法 FedBag 在收敛效率上的优势，即收敛过程稳定且能更快达到目标识别率，此外展示了指定通信时限的不同对 FedBag 的性能影响。

2 系统模型

假设网络共有K个节点，每个节点k有一个数据量为nk的本地数据集。本文以图像识别任务的应用场景为例，节点 k 的标签分布可用标签向量 ZkZk来描述。

Zk=[nk,1,nk,2,⋯,nk,C]　　　　(1)Zk=[nk,1,nk,2,⋯,nk,C]　　　　(1)

其中，C 表示标签种类总数，nk,C表示节点 k 拥有的第C类图像的张数。

联邦学习往往假设训练数据由节点本地产生，因此，节点间的标签分布会随设备使用习惯而产生差异，即服从非独立同分布（non independent identically distributed, NON-IID）。服务器希望利用节点的本地数据训练出一个全局模型，因此，优化目标是求解下述优化问题的最优模型参数ω*。

ω*=argmin ω ​​​​​F(ω,S)=argminω ​​​​​​1|S|∑k=1Knk​f(ω,sk)　　(2)ω*=argmin ω ​​​​​F(ω,S)=argminω ​​​​​​1|S|∑k=1Knk​f(ω,sk)　　(2)

其中，f(ω,sk)是节点k 利用本地数据集sk求得的损失函数，而F(ω,S)则为全局损失函数，在图像识别任务中常采用交叉熵作为损失函数。

联邦学习的基本流程为：假设在每回合开始训练前各节点向服务器提供了其标签向量ZZ与各自的上传时间估计 TUL与训练时间估计 TUD，本文假设通信过程是顺序上传的，因此，时间估计可根据具体信道条件与通信量计算求得。

步骤 1 分发：服务器选择这一回合参与训练的节点，然后进行全局模型的分发。

步骤 2 本地训练：节点收到全局模型后，用本地数据对模型进行训练，求得本地模型。

步骤3 上传：节点向服务器上传本地模型参数。

步骤 4 汇总：服务器收到来自各节点的本地模型后，根据更新公式求得新的全局模型。

步骤5 重复步骤1～步骤4，直到全局模型性能达到任务要求。

3 算法设计

3.1 优化目标

由于联邦学习中节点的训练数据一般由本地产生且节点间不进行数据互通，与传统分布式训练不同的是节点间的数据分布规律会因设备使用习惯的不同而产生差异，而节点数据的NON-IID程度越高，联邦学习的算法性能会相应下降，因为节点的本地模型更新方法也因其数据分布而发生相对于全局方向的偏移。为了克服这一问题，现有算法一般借助节点训练后的本地模型参数，选择模型更新偏移较小的样本进行全局模型的更新，具体来说可通过式(3)的权重偏移（weight divergence）[13]衡量不同节点样本的质量。其中，ωf表示联邦学习的全局模型参数，ωc表示能代表全局方向的参照模型参数，可根据一个能代表全局分布的参照数据集，通过传统集中式训练求得。但这类方法必须在节点完成训练后才进行优化工作，且往往需要选择额外的节点参与训练，再从中选择实际参与更新的一部分节点，这一过程会产生额外的通信与训练成本。

weight divergence=∥ωf−ωc∥/∥ωc∥　　　　(3)weight divergence=‖ωf−ωc‖/‖ωc‖　　　　(3)

文献[13]分析了 FedAvg 算法中节点数据分布与全局模型收敛之间的关系，提出了一个关于节点标签分布的参量EMD（earth-mover’s distance）[13]，其具体数学形式为

EMDk=∑i=1C∥∥pky=i−py=i∥∥　　　　(4)EMDk=∑i=1C‖py=ik−py=i‖　　　　(4)

其中，pky=ipy=ik表示组合内节点k的第i类数据的分布概率，py=ipy=i表示第 i 类数据的全局分布概率，因此， EMD 能反映节点的标签分布相对于全局分布的差异。文献[13]提出了其与联邦学习权重偏移上界之间的关系，而本文注意到相较于直接利用模型参数求得的权重偏移，标签量的信息量低，计算简单且能在节点开始训练前获取，有能与通信条件等指示信息相结合、更好改良算法通信性能的优势。因此，本文考虑将标签量信息作为节点选择指示信息的新思路，但直接利用 EMD 作为指示信息存在一定缺陷，这点可从如图1所示的三选二的节点选择情境下联邦学习的模型收敛示意图直观分析。其中， ω 表示模型的权重参数或可以理解为模型更新方向，其上标表示节点，下标表示回合数，假设节点1、2、3 的 EMD 值从小到大排序，因此，更新方向依次更接近于全局方向。上标f1、f2分别表示选择节点组合1、2与1、3两种方案所得的全局模型，可见优先选择EMD较优的组合1、2的方案并非最优，因为 EMD 仅能反映单一节点的信息而无法综合反映一个节点组合对全局模型收敛的综合影响。

图1

图1   三选二的节点选择情境下联邦学习的模型收敛示意图

文献[14]提出了 GEMD（group earth-mover’s distance）的参量，可用于衡量一个节点组合ζ的标签分布与全局分布间的差异。具体数学形式如下

GEMDζ=∑i=1C∥∥∥∥∥∥∑k∈ζnkpky=i∑k∈ζnk−py=i∥∥∥∥∥∥　　　　(5)GEMDζ=∑i=1C‖∑k∈ζnkpy=ik∑k∈ζnk−py=i‖　　　　(5)

GEMD的概念由EMD发展而来，而GEMD反映了一个节点组合的综合标签分布与全局分布的距离，因此更适合于作为节点选择的指示信息。在文献[13]的基础上，本文进一步提出了在 NON-IID的节点数据分布下 GEMD 与联邦学习的全局模型的权重偏移上界的关系

∥∥ωfL−ωcL∥∥≤(α)L∥∥∥∥∑k∈ζnk∑k∈ζnkωk0−ωc0∥∥∥∥+‖ωLf−ωLc‖≤(α)L‖∑k∈ζnk∑k∈ζnkω0k−ω0c‖+

        ∑t=0L−1gmax(ωkt)∑i=1C∥∥∥∥∥∥∑k∈ζnkpky=i∑k∈ζnk−py=i∥∥∥∥∥∥        ∑t=0L−1gmax(ωtk)∑i=1C‖∑k∈ζnkpy=ik∑k∈ζnk−py=i‖

此处

 gmax(ωkt)=max1≤i≤C1≤k≤K(λx|y=i∥∥ωkt∥∥),  gmax(ωtk)=max1≤i≤C1≤k≤K(λx|y=i‖ωtk‖), 

 (α)L=(1+η∑i=1Cpy=iλx|y=i)L　　　　(6) (α)L=(1+η∑i=1Cpy=iλx|y=i)L　　　　(6)

其中，不等式左项表示联邦学习的全局模型在经过L 回合节点本地训练后，与传统集中式学习模型之间的权重偏移，损失函数为交叉熵且假设其满足λ-lipschit条件。式(6)反映联邦学习的权重偏差上界主要受初始模型参数的差异，以及节点数据的分布差异影响，具体反映为其中的GEMD参量。因此，式(6)为 GEMD 作为节点选择的指示信息提供了理论依据。

接下来考虑如何利用 GEMD 设计新的节点选择算法，优化目标是减轻节点的数据分布差异对模型收敛的不良影响，从而改善联邦学习算法的收敛性能。本文的优化目标可描述为

argminζ∥∥Zζ||Zζ||−Zglobal||Zglobal||∥∥,s.t.θζ<Tlimit　　　　(7)argminζ‖Zζ||Zζ||−Zglobal||Zglobal||‖,s.t.θζ　　　　(7)

此处 Zζ=∑k∈ζZkZζ=∑k∈ζZk ， Zglobal=∑Kk=1ZkZglobal=∑k=1KZk

其中，ZζZζ表示节点组合的标签向量之和，ZglobalZglobal表示全局标签向量，θζ表示节点组合的总耗时估计， Tlimit表示回合耗时上限。将节点的标签向量作为其标签分布的估计的话，式(7)的物理意义即节点组合的 GEMD 值。因此优化目标为找到耗时上限 Tlimit内，GEMD值最低的节点组合。

3.2 设计思路

结合式(1)的优化目标，优化难点主要有两点：一是GEMD是关于节点组合标签向量的非线性函数，且与通信时间估计等具有较强的独立性，虽然可以通过遍历求得最优解，但其搜索复杂度太高；二是如何根据节点提供的训练时间估计TUD与上传时间估计TUL，快速计算出不同节点组合的总耗时。

关于第一个问题，本文考虑设计一个近似算法，牺牲一定的精度换取更高的搜索效率。具体而言，本文采取一个顺序考虑向已选组合添加节点，且不替换先前已选节点的方法。该简化搜索过程仅需一次遍历即可完成搜索，缺点是具体搜索结果会受节点考虑顺序的影响，因此，每回合算法在开始时需要打乱节点考虑顺序。

在此基础上，考虑第二个优化难题，仅需求得添加当前节点的新增耗时，结合已选节点组合的耗时估计，即可快速求得不同节点组合的耗时估计。因此，本文假设所有被选节点完成训练后，再顺序上传其本地模型参数。具体地，本文只考虑受节点差异影响较大的节点训练耗时与模型参数上传耗时的该部分时间，不同节点组合的计算方法为

θζ=TUDζ+∑k∈ζTULkθζ=TζUD+∑k∈ζTkUL

其中，

TUDζ=maxk∈ζTUDk　　　　(8)TζUD=maxk∈ζTkUD　　　　(8)

因为实际任务中不同节点的训练与上传任务可并行处理，上述简化计算方法能保证大于实际耗时，且好处是简化了向组合内添加节点k的新增耗时ΔTk的计算复杂度。具体方法为

ΔTk=TULk+max(0,TUDk−TUDζ)　　(9)ΔTk=TkUL+max(0,TkUD−TζUD)　　(9)

因此，只需保存当前节点组合的最大训练耗时即可求得ΔTk。

3.3 算法描述

本文将矩阵作为主要的数据结构，用于存储不同节点组合的关键变量，建立了 4 个大小为(K+1)行Tlimit列的矩阵，矩阵的每个元素表示一个节点组合，其中，价值矩阵Mvalue存储节点组合的当前GEMD价值，标签矩阵 M label存储当前组合标签向量 Zζ，训练时间矩阵MTUD存储节点组合的最大训练时间，耗时矩阵MTζMTζ 存储节点组合的总耗时估计。矩阵的第0行元素初始化为0表示空状态，然后搜索过程为逐个更新矩阵内元素，保存当前价值最优的节点组合，记录其变量信息。

通过一个两层循环算法实现搜索：服务器从第1行开始逐个考虑添加节点，行坐标为外循环，列坐标为内循环，比较将该节点添加进上一轮的更新结果后形成的新组合是否更优。最终输出的矩阵中第i行、第j列的元素对应了一个第i次更新后总时耗小于 j 的节点组合方案。各矩阵的更新的公式为

Mvalue(i,j)={min(∥∥Znew∥Znew∥−Zglobal∥Zglobal∥∥∥,Mvalue(i−1,j))  ,j≥ΔTi                   Mvalue(i−1,j)                      ,j<ΔTi　　(10)Mvalue(i,j)={min(‖Znew‖Znew‖−Zglobal‖Zglobal‖‖,Mvalue(i−1,j))  ,j≥ΔTi                   Mvalue(i−1,j)                      ,j<ΔTi　　(10)

其中， Znew=Zi+Mlabel(i−1, j−ΔTi)Znew=Zi+Mlabel(i−1, j−ΔTi)。

Mlabel(i,j)={Znew       ,Mvalue(i,j)≠Mvalue(i−1,j)Mlabel(i−1,j) ,Mvalue(i,j)=Mvalue(i−1,j)　　　　(11)Mlabel(i,j)={Znew       ,Mvalue(i,j)≠Mvalue(i−1,j)Mlabel(i−1,j) ,Mvalue(i,j)=Mvalue(i−1,j)　　　　(11)

MTUD(i,j)=⎧⎩⎨⎪⎪ max(MTUD(i−1,j−ΔTi),TUDi) ,Mvalue(i,j)≠Mvalue(i−1,j)MTUD(i−1,j) ,Mvalue(i,j)=Mvalue(i−1,j)　　　　(12)MTUD(i,j)={ max(MTUD(i−1,j−ΔTi),TiUD) ,Mvalue(i,j)≠Mvalue(i−1,j)MTUD(i−1,j) ,Mvalue(i,j)=Mvalue(i−1,j)　　　　(12)

MTζ(i,j)=⎧⎩⎨⎪⎪⎪⎪MTζ(i−1,j−ΔTi)+ΔTi ,Mvalue(i,j)≠Mvalue(i−1,j)MTζ(i−1,j)   ,Mvalue(i,j)=Mvalue(i−1,j)　　　　(13)MTζ(i,j)={MTζ(i−1,j−ΔTi)+ΔTi ,Mvalue(i,j)≠Mvalue(i−1,j)MTζ(i−1,j)   ,Mvalue(i,j)=Mvalue(i−1,j)　　　　(13)

其中，ZnewZnew表示往上一轮的已有组合中添加当前考虑的节点i后，时耗小于或等于j的新节点组合的标签向量和。因此，搜索节点组合的过程如下：各节点逐次考虑放入被选列表中，比较将该节点添加进上一轮的更新结果后形成的新组合是否更优，保留 GEMD 较低的方案，将其对应的各项变量存储到各矩阵中。为了使用矩阵作为数据结构，节点的新增用时Δ Tk与组合通信时限Tlimit需要进行量化取整的处理，本文采取以秒为单位的量化，四舍五入的取整法，其中，存在着利用合理的量化方案来简化矩阵大小的优化空间，还待进一步研究。

本方法考虑了对节点进行时间估计后如何选取出 GEMD 尽可能最优的节点组合的优化问题，采取了一个依次考虑向已选组合添加节点且不考虑替换的搜索方法，在时耗上限为Tlimit、节点数为K的系统下，搜索过程的复杂度为Ο(KTlimit)。新算法的好处是能够在稳定控制联邦学习算法每回合通信时间的同时，利用GEMD与全局模型收敛的相关性对联邦学习算法的收敛性能进行改良，不足之处是算法采取的节点组合搜索方法是一种简化的方案，难以得到所要解决优化问题的最优解。虽然算法的实现过程与动态规划算法类似，但实际优化问题与经典背包问题有所不同，由于GEMD是一个非线性函数，无法通过递推求得最优解，即本算法属于近似算法而非最优化算法。即新算法并不能稳定选出优化问题的最优解。本文将新算法命名为类背包节点选择算法（FedBag），见算法1。

算法 1 基于标签量信息的类背包节点选择算法FedBag

输入 节点标签向量ZkZk，训练时间估计TUDkTkUD，上传时间估计TULkTkUL，回合时耗上限Tlimit

初始化 价值矩阵MvalueMvalue ，标签矩阵MlabelMlabel，训练用时矩阵MTUDMTUD，上传用时矩阵MTULMTUL，ζ={}

打乱节点从 1～K 的顺序，各节点的标签向量与时间估计之间的对应关系保持不变。

以节点坐标进行一层循环：

以时间从1到Tlimit进行二层循环：

计算ΔTk=TULk+max(0,TUDk−TUDζ)ΔTk=TkUL+max(0,TkUD−TζUD)

根据式（10）～式（13）更新4个矩阵

遍历价值矩阵，将值发生变化的节点坐标k加入待选列表ζ

输出 被选列表ζ

4 仿真分析

4.1 仿真设置

本文的仿真实验是以卷积神经网络模型FEMNIST[15]图像集的图像识别任务为基础，模型包括两个5×5卷积核大小的卷积层、一个最大池化层、两个全连接层和一个Softmax输出层。损失函数选用的是交叉熵。而仿真实验是在虚拟环境下进行的，通过设置一系列拥有不同本地数据的虚拟节点，每回合服务器选择参与训练的节点更新全局模型。程序实现基于TensorFlow框架，具体可分为服务器部分与节点部分。其中，服务器部分中各功能模块是按照第2节介绍的联邦学习基本流程来设计的；节点部分的主要功能为模型训练。联邦学习流程中服务器与节点间的通信过程是通过建立信道模型模拟的，模型可用于求得一个各节点传输时耗的估计值。比较不同节点选择方法下的仿真系统输出的训练结果，可验证本文所提的节点选择算法的性能。

假设系统中有K=200个节点，每个节点随机拥有2到4种标签的训练数据，每种类型的数据量通过一个均值为 50 的指数正态分布函数随机选取。在节点的时耗估计中，本节参考文献[3]的设置，通信模型是基于LTE网络建模的，在ITU-R M.2135-1六边形小区布局的微NLOS模型中定义的一个著名的城市信道模型。载频为2.5 GHz，基站和节点端的天线高度分别设置为11 m和1 m。假设基站和节点端的发射功率和天线增益分别为20 dBm和0 dBi。吞吐量的计算方法参考了文献[16]，最终计算出的节点平均与最大吞吐量分别为1.4 Mbit/s与7.4 Mbit/s。传输的数据量为模型参数的实际比特数，因此可根据信道容量与传输量计算出各节点的上传时间估计。而本节将各节点的计算能力通过一个均值为10的指数正态分布随机生成，表示每秒能处理完多少个数据，也因此可根据各节点的数据量与计算能力求得训练时间估计。在节点选择环节中，基于上述的节点标签分布信息以及计算得出的节点时耗估计，新节点选择算法 FedBag 便可正常运行，求得接下来进行本地训练以及全局模型更新的节点列表。在本地训练环节中，节点更新采用 mini-batch SGD的训练方法，batch大小设置为10，局部迭代次数设置为 5。全局模型的汇总更新选择了FedAvg[1]的更新公式，一种基于数据量的节点本地更新样本的加权平均法。

为了展示新节点选择算法FedBag的性能，本节选择了 3 个现有节点选择算法作为对照对象：一是随机选择（RS, random selection），服务器以等概率随机选取若干节点参与训练；二是穷举法（EM, exhaustive method），通过遍历所有可能组合来求得GEMD表现最优的节点组合，其优化目标同样如式(7)所示。为了简化复杂度EM仅遍历最多由5个节点组成的组合，此时复杂度为Ο(K5)；三是 FedCS[3]，以节点选择数最大为优化目标的贪心算法，服务器逐一选出时耗最低的节点直到时耗上限，因此拥有与排序算法类似的复杂度Ο(K2)。本节比较了4种节点选择方法在运行指定总时耗后，在 FedAvg 算法的全局模型更新公式下的识别率与损失函数曲线，其中，RS的选择节点数为10，其余方法的单回合节点组合时耗上限设为200 s。

4.2 仿真结果

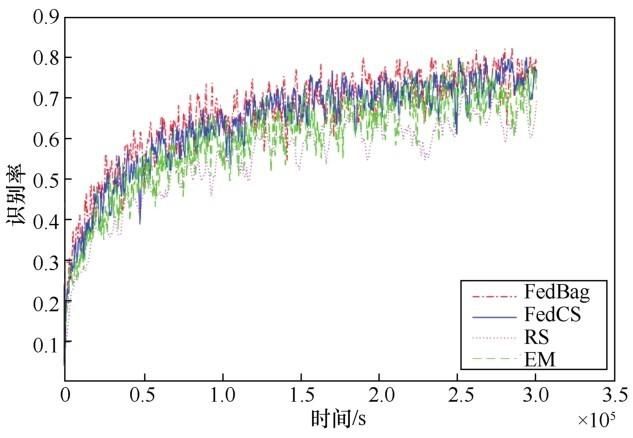
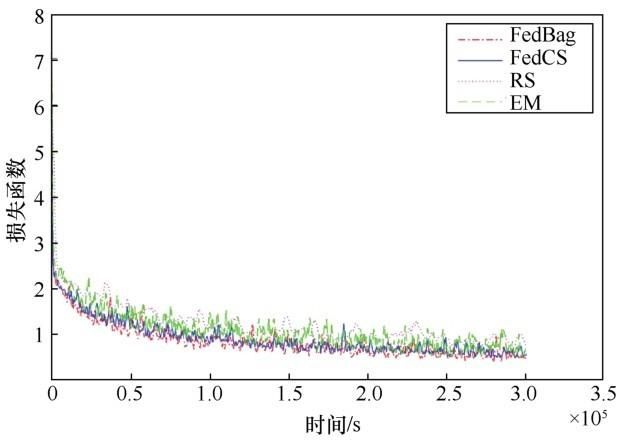
图2、图3分别为4种节点选择算法在FedAvg更新公式下的性能表现，横轴表示回合累积时耗，纵轴分别表示识别率与损失函数。此不同方法的具体运行回合数与到达目标识别率的所需耗时见表1。其中，RS 表现最差，因为随机选择的方法未考虑节点间数据与通信条件的差异，容易选中条件较差的节点，增大每回合的训练时耗从而影响全局性能。从运行回合数对比中可看出其余3个算法在限制回合时耗上的有效性。而本文提出的 FedBag 算法不仅相较于 RS，比起以节点数的优化目标的FedCS算法而言有着更高的收敛速率。这是因为仿真设置中假设了节点数据量与标签种类数成正比，因此数据量较大的节点对全局模型收敛的作用更大，而FedCS的优先选择耗时最低的节点的策略容易忽略在时限内但耗时较大的节点，而 FedBag 不会存在这个问题。这也反映了 GEMD 比起节点数更适合作为节点选择的指示信息。而EM算法的收敛过程波动比较明显，在整体上表现出一个先劣后优的性能，因为在训练前期 EM 方法的所选节点数较低，在训练难度较低的情况下被选节点数或数据量为影响模型收敛效率的主要因素。从表1可看出，从离散点观察EM与FedCS相比也有一个小幅的性能优势。虽然 FedBag 求得的是近似解，但在复杂度远低于穷举法的情况下，有着不劣于EM的性能表现。

图2

图2   FedBag、FedCS、RS、EM 4种节点选择算法的识别率曲线

 

图3

图3   FedBag、FedCS、RS、EM 4种节点选择算法的损失函数曲线

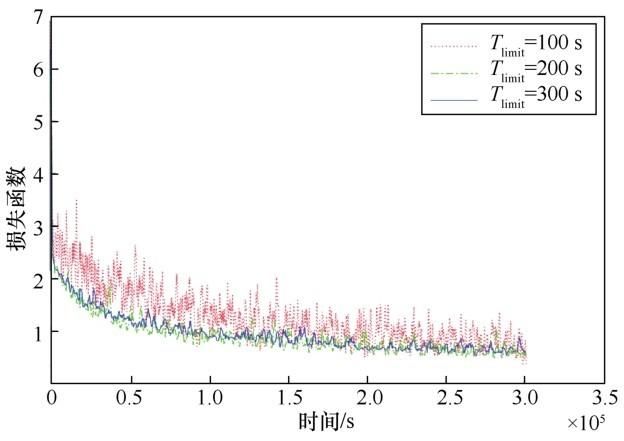
作为影响性能的关键参量，图4、图5分别展示了不同 Tlimit下 FedBag 节点选择方法在 FedAvg更新公式下的识别率与损失函数曲线，具体运行回合数与到达目标识别率的所需耗时见表2。可见Tlimit越高，模型收敛过程越稳定，到达目标识别率的所需耗时也会随之增加，说明回合数对模型收敛速率起着关键作用，实际应用中Tlimit的设置需要考虑收敛速率与稳定性之间的权衡。

表1   4种节点选择算法的运行回合数与到达目标识别率耗时的统计

算法名	运行回合总数			到达目标识别率耗时
		50%	60%	70%	80%	85%
FedBag	1 169	3.924 2 h	6.111 9 h	17.152 5 h	31.633 3 h	59.159 9 h
FedCS	1 235	5.038 0 h	9.479 3 h	20.023 8 h	44.540 4 h	78.161 5 h
RS	364	11.506 3 h	19.463 7 h	45.226 8 h	111.395 5 h	207.675 1 h
EM	1 398	3.881 7 h	7.988 1 h	13.445 8 h	42.140 8 h	66.910 1 h

表2   不同Tlimit下FedBag运行回合数与到达目标识别率耗时的统计

Tlimit/s	运行回合总数			到达目标识别率耗时
		50%	60%	70%	80%	85%
100	2320	2.9230 h	4.3990 h	9.8239 h	21.2913 h	28.4150 h
200	1169	3.9242 h	6.1119 h	17.1525 h	31.6333 h	59.1599 h
300	872	3.3955 h	9.0295 h	16.4829 h	43.4716 h	78.7371 h

 

图4

图4   FedBag在不同Tlimit下的识别率曲线

 

图5

图5   FedBag在不同Tlimit下的损失函数曲线

 

5 结束语

本文提出了一种基于标签量信息的类背包节点选择算法 FedBag，以选择出一定时耗内标签分布尽可能均匀的节点组合为优化目标，采取了一种逐个向已选组合添加节点的简化搜索方法。经仿真验证相较于原始的随机选择策略与以节点数为贪心目标的现有节点选择算法而言，FedBag 能更好地提高联邦学习算法的收敛性能、更快地达到目标识别率。而不足之处在于算法采取的是一种近似算法，具体近似程度还有待证明，且算法的一些细节还有待改善，包括可能存在重复比对相同组合导致算法效率的下降等。标签量信息作为节点选择指示信息的思路还存在很多发展空间，除了GEMD外还有诸如数据量等数据也影响着联邦学习全局模型的收敛过程，如何更好地利用标签量信息也是未来值得关注的问题。