机器学习(周志华) 第五章神经网络
关于周志华老师的《机器学习》这本书的学习笔记
记录学习过程
本博客记录Chapter5 神经网络
文章目录
- 1 神经元模型
- 2 感知机与多层网络
- 3 误差逆传播算法(BP)
- 4 全局最小和局部极小
- 5 其他常见神经网络
-
- 5.1 RBF网络
- 5.2 ART网络
- 5.3 SOM网络
- 5.4 级联相关网络
- 5.5 Elman网络
- 5.6 Boltzmann机
- 6 深度学习
1 神经元模型
神经网络(neural networks):由具有适应性的简单单元组成的广泛并行互联的网络,他的组织能够模拟生物神经系统对真实世界物体所做出的交互反应。
神经网络中最基本的成分是“神经元模型”,即上述定义中的“简单单元”。经典的M-P神经元模型如下图所示。其中,神经元(neural)接收到 n n n个其他神经元传递过来的输入信号,这些输入信号通过带权重的连接(connection)进行传递,神经元接收到的总输入值将与神经元的阈值进行比较,然后通过激活函数(activation function)处理以产生神经元的输出。
理想中的激活函数如下图所示的阶跃函数,其将输入值映射为输出值0或1,1对神经元产生刺激,0对神经元产生抑制。但阶跃函数具有不连续、不光滑等缺点,因此实际中常用Sigmoid函数作为激活函数,它能在较大范围内变化的输入值挤压到 ( 0 , 1 ) (0,1) (0,1)之间也被称为“挤压函数”(squashing function),其公式如下:
s g n ( x ) = { 1 , x ≥ 0 0 , x ≤ 0 sgn(x)=\begin{cases} 1, x\ge 0\\ 0, x\le 0\\ \end{cases} sgn(x)={1,x≥00,x≤0
s i g m o i d ( x ) = 1 1 + e − x sigmoid(x)=\frac{1}{1+e^{-x}} sigmoid(x)=1+e−x1
将神经元按照一定的层次结构连接起来,就组成了神经网络。神经网络包含了许多参数的数学模型,这个模型是若干个函数相互嵌套代入所得。有效的神经网络模型大多以数学证明为支撑。
2 感知机与多层网络
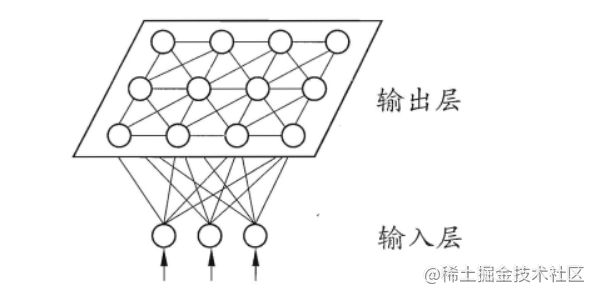
感知机(perceptron)由两层神经元组成。输入层接受外界输入信号后传递给输出层,输出层是M-P神经元,也成为“阈值逻辑单元”(threshold logic unit)。能容易地实现与或非的运算。其中 y = f ( ∑ i w i x i − θ ) y=f(\sum_iw_ix_i-\theta) y=f(∑iwixi−θ), f f f假设为阶跃函数。
- 与运算: w 1 = 1 , w 2 = 1 , θ = 2 , 有 y = f ( x 1 + x 2 − 2 ) , 当 且 仅 当 x 1 = x 2 = 1 时 , y = 1 w_1=1,w_2=1,\theta=2,有y=f(x_1+x_2-2),当且仅当x_1=x_2=1时,y=1 w1=1,w2=1,θ=2,有y=f(x1+x2−2),当且仅当x1=x2=1时,y=1
- 或运算: w 1 = 1 , w 2 = 1 , θ = 0.5 , 有 y = f ( x 1 + x 2 − 2 ) , 当 且 仅 当 x 1 = x 2 = 0 时 , y = 0 w_1=1,w_2=1,\theta=0.5,有y=f(x_1+x_2-2),当且仅当x_1=x_2=0时,y=0 w1=1,w2=1,θ=0.5,有y=f(x1+x2−2),当且仅当x1=x2=0时,y=0
- 非运算: w 1 = − 0.6 , w 2 = 0 , θ = − 0.5 , 有 y = f ( x 1 + x 2 − 2 ) , 当 x 1 = 1 时 , y = 0 ; 当 x 1 = 0 时 , y = 1 w_1=-0.6,w_2=0,\theta=-0.5,有y=f(x_1+x_2-2),当x_1=1时,y=0;当x_1=0时,y=1 w1=−0.6,w2=0,θ=−0.5,有y=f(x1+x2−2),当x1=1时,y=0;当x1=0时,y=1
当给定训练数据,权重 w i w_i wi以及阈值 θ \theta θ都可以通过学习得到。阈值可以看作一个固定输入为-1的“哑结点”(dummy node)所对应的连接权重 w n + 1 w_{n+1} wn+1。这样,权重和阈值的学习可以统一为权重的学习。感知机的学习规则如下:训练样例 ( x , y ) (\bold{x},y) (x,y),若当前感知机的输出为 y ^ \hat{y} y^,则感知机的权重调整为:
w i ← w i + Δ w i Δ w i = η ( y − y ^ ) x i w_i \leftarrow w_i+ \Delta w_i \\ \Delta w_i = \eta(y-\hat{y})x_i wi←wi+ΔwiΔwi=η(y−y^)xi
其中, η \eta η是学习率,感知机对预测数据的错误的程度进行权重调整。实际中,感知机只有输出层神经元进行激活函数处理,即只用有一层功能神经元(functional neural),能解决的只有线性可分问题(与或非都是此类问题)。对于线性可分问题,感知机的学习过程一定会收敛,球的适当的权向量 w = ( w 1 ; w 2 ; … ; w n + 1 ) \bold w=(w_1;w_2;…;w_{n+1}) w=(w1;w2;…;wn+1)。否则,感知机学习过程将会发生振荡, w \bold w w难以稳定,即使是异或这样简单的非线性可分问题也无法解决。
- 异或:二进制中每一位进行异或运算,不同为1,相同为0,如 ( 0011 ) (0011) (0011)和 ( 1010 ) (1010) (1010)异或后是 ( 1001 ) (1001) (1001)

两层感知机可以解决异或问题,其在输入层与输出层之间添加一层神经元,称为隐含层(hidden layer),隐含层和输出层神经元都是拥有激活函数的功能神经元。
多层前馈神经网络(multi-layer feedforward neural networks):每层神经元与下层神经元完全互连,神经元之间不存在同层连接,也不存在跨层连接。
- 输入层仅接受输入,不进行函数处理,隐层和输出层有激活函数,包含功能神经元。
- 神经网络的学习过程,就是根据训练数据来调整神经元之间的“连接权”(connection weight)以及每个功能神经元的阈值;即神经网络“学到的东西”,驯悍在连接权和阈值中。
3 误差逆传播算法(BP)
误差逆传播(error BackPropagation, BP)算法是最成功的神经网络学习算法,能有效地训练多层网络。
其算法原理:
- 假定训练集 D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } , x i ∈ R d , y i ∈ R l D=\{(\bold x_1,\bold y_1), (\bold x_2,\bold y_2),…,(\bold x_m,\bold y_m) \},\bold x_i \in R^d, \bold y_i \in R^l D={(x1,y1),(x2,y2),…,(xm,ym)},xi∈Rd,yi∈Rl,即输入由 d d d个属性描述,输出由 l l l个维实值向量描述。神经网络结构如图所示,拥有 d d d个输入神经元、 l l l个输出神经元、 q q q个隐层神经元的多层前馈网络结,其中输出层第 j j j个神经元的阈值用 θ j \theta_j θj表示,隐层第 h h h个神经元的阈值用 γ h \gamma_h γh表示。输入层第 i i i个神经元与隐层第 h h h个神经元之间的连接权为 v i h v_{ih} vih,隐层第 h h h个神经元与输出层第 j j j个神经元之间的连接权为 w h j w_{hj} whj。记隐层第 h h h个神经元接收到的输入为 α h = ∑ i = 1 d v i h x i \alpha_h= \sum_{i=1}^dv_{ih}x_i αh=∑i=1dvihxi,输出层第 j j j个神经元接收到的输入为 β j = ∑ i = 1 q w h j b h \beta_j=\sum_{i=1}^qw_{hj}b_h βj=∑i=1qwhjbh, 其中 b h b_h bh为隐层第 h h h个神经元的输出。假设隐层和输出层神经元都使用Sigmoid函数。
-
对训练例 ( x k , y k ) (\bold x_k, \bold y_k) (xk,yk),假定神经网络的输出 y k ^ = ( y ^ 1 k , y ^ 2 k , … , y ^ l k ) \hat{y_k}=(\hat y_1^k,\hat y_2^k,…,\hat y_l^k) yk^=(y^1k,y^2k,…,y^lk),即
y k ^ = f ( β j − θ j ) \hat{y_k}=f(\beta_j-\theta_j) yk^=f(βj−θj)
则网络在 ( x k , y k ) (\bold x_k, \bold y_k) (xk,yk)上的均方误差为
E k = 1 2 ∑ j = 1 l ( y ^ j k − y j k ) 2 E_k=\frac{1}{2}\sum_{j=1}^l(\hat{y}_j^k-y_j^k)^2 Ek=21j=1∑l(y^jk−yjk)2 -
该网络共有 d q + q l + q + l = q ( d + l + 1 ) + l dq+ql+q+l=q(d+l+1)+l dq+ql+q+l=q(d+l+1)+l个参数需要确定,BP是一个迭代学习算法,每一轮迭代中采用广积的感知机学习规则对参数进行更新估计
v ← v + Δ v v \leftarrow v+\Delta v v←v+Δv -
BP算法基于梯度下降策略(gradient descent):以目标的负梯度方向对参数进行调整。对误差 E k E_k Ek,给定学习率 η \eta η,有
Δ w h j = − η ∂ E k ∂ w h j ∂ E k ∂ w h j = ∂ E k ∂ y ^ j k ⋅ ∂ y ^ j k ∂ β j ⋅ ∂ β j ∂ w h j \Delta w_{hj}=-\eta \frac{\partial E_k}{\partial w_{hj}}\\ \frac{\partial E_k}{\partial w_{hj}}=\frac{\partial E_k}{\partial \hat{y}_j^k}·\frac{\partial \hat y_j^k}{\partial \beta_j} ·\frac{\partial \beta_j}{\partial w_{hj}} Δwhj=−η∂whj∂Ek∂whj∂Ek=∂y^jk∂Ek⋅∂βj∂y^jk⋅∂whj∂βj
根据 β j \beta_j βj的定义: ∂ β j ∂ w h j = b h \displaystyle \frac{\partial \beta_j}{\partial w_{hj}}=b_h ∂whj∂βj=bhSigmoid函数具有性质:
f ′ ( x ) = f ( x ) [ 1 − f ( x ) ] f'(x)=f(x)[1-f(x)] f′(x)=f(x)[1−f(x)]
因此:
g j = − ( y ^ j k − y j k ) f ′ ( β j − θ j ) = y ^ j k ( 1 − y ^ j k ) ( y j k − y ^ j k ) g_j=-(\hat y_j^k-y_j^k)f'(\beta_j-\theta_j)=\hat y_j^k(1-\hat y_j^k)(y_j^k-\hat y_j^k) gj=−(y^jk−yjk)f′(βj−θj)=y^jk(1−y^jk)(yjk−y^jk)
将上述式子带入到 Δ w h j \Delta w_{hj} Δwhj:
Δ w h j = η g j b h \Delta w_{hj}=\eta g_j b_h Δwhj=ηgjbh
类似可得:
Δ θ j = − η g i Δ v i h = η e h x i Δ γ h = − η e h \Delta \theta_j=-\eta g_i\\ \Delta v_{ih} = \eta e_h x_i\\ \Delta \gamma_h=-\eta e_h Δθj=−ηgiΔvih=ηehxiΔγh=−ηeh
其中,
e h = − ∂ E k ∂ b h ⋅ ∂ b h ∂ α h = − ∑ i = 1 l ∂ E k ∂ β j ∂ β j ∂ b h f ′ ( α h − γ h ) = ∑ j = 1 l w h j g j f ′ ( α j − γ j ) = b h ( 1 − b h ) ∑ j = 1 l w h j g j e_h=-\frac{\partial E_k}{\partial b_h}·\frac{\partial b_h}{\partial \alpha_h}=-\sum_{i=1}^l \frac{\partial E_k}{\partial \beta_j} \frac{\partial \beta_j}{\partial b_h}f'(\alpha_h-\gamma_h)=\sum_{j=1}^lw_{hj}g_jf'(\alpha_j-\gamma_j)=b_h(1-b_h)\sum_{j=1}^lw_{hj}g_j eh=−∂bh∂Ek⋅∂αh∂bh=−i=1∑l∂βj∂Ek∂bh∂βjf′(αh−γh)=j=1∑lwhjgjf′(αj−γj)=bh(1−bh)j=1∑lwhjgj -
学习率 η ∈ ( 0 , 1 ) \eta \in (0,1) η∈(0,1)控制着算法每一轮迭代的更新步长,太小收敛速度会过慢,太大容易发生振荡。
BP算法流程:
标准BP算法: 基于每个数据进行更新,参数更新频繁,而且对不同的样例进行更新的效果可能出现抵消现象。
累积BP算法: 直接针对累积误差最小化。读取整个训练集D一遍后才对参数进行更新,其参数更新频率较低,但累计误差下降到一定程度后,进一步下降会非常缓慢,这时候标准BP往往会更快获得较好的解。
min E = 1 m ∑ i = 1 m E k \min E=\frac{1}{m}\sum_{i=1}^mE_k minE=m1i=1∑mEk
BP神经网络经常遭遇“过拟合”的现象,有两种解决方法:
-
“早停”(early stopping):将数据集分成训练集和验证集,训练集用来计算梯度、更新连接权和阈值,验证机用来估计误差,若训练集误差降低而测试集误差升高,则停止训练。
-
“正则化”(regularization):在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权和阈值的平方和,其中 λ \lambda λ用于经验误差和网络复杂度两项进行折中,通过交叉验证法估计。
E = λ 1 m ∑ i = 1 m E k + ( 1 − λ ) ∑ i w i 2 E=\lambda \frac{1}{m}\sum_{i=1}^m E_k+(1-\lambda)\sum_i w_i^2 E=λm1i=1∑mEk+(1−λ)i∑wi2
4 全局最小和局部极小
基于梯度的搜索是使用最广泛的参数寻优方法。
在此类方法中,我们从某些初始解出发,迭代寻找最优参数值。每次迭代中,我们计算误差函数在当前点的梯度,然后根据梯度确定搜索方向。由于负梯度方向是函数值下降最快的方向,因此梯度下降法就是沿着负梯度方向搜索最优解。若误差函数在当前点的梯度为0,则达到局部极小,迭代停止。因此,该方法可能会陷入局部极小,无法达到全局最小。
跳出“局部极小”的方法(大多是启发式算法,理论上缺乏保障):
- 以多组不同参数值初始化神经网络,取误差最小的解作为参数。
- 使用“模拟退火”,每一步都以一定的概率接受比当前解更差的结果,从而有助于跳出局部极小,每步迭代过程中,接受“次优解”的该列表随着时间的推移而逐渐降低,从而保证算法稳定。
- 随机梯度下降:在计算梯度时加入随机因素,所以即便陷入局部最小,计算出的梯度可能不为0,有机会跳出局部极小。
5 其他常见神经网络
5.1 RBF网络
RBF(Radial Basis Function,径向基函数)网络:单隐层前馈神经网络,使用径向基函数作为隐层神经元激活函数,输出层是对隐层神经元输出的线性组合。高级径向基函数似如:
φ ( x ) = ∑ i = 1 q w i ρ ( x , c i ) ρ ( x , c i ) = e − β i ∣ ∣ x − c i ∣ ∣ 2 \varphi(x)=\sum_{i=1}^qw_i\rho(\bold x, \bold c_i)\\ \rho(\bold x, \bold c_i)=e^{-\beta_i||\bold x-\bold c_i||^2} φ(x)=i=1∑qwiρ(x,ci)ρ(x,ci)=e−βi∣∣x−ci∣∣2
径向基函数是沿径向对称的标量函数,定义为样本 x \bold x x与数据中心 c i \bold c_i ci之间的欧氏距离。
5.2 ART网络
竞争性学习(competitive learning)是神经网络中常用的一种无监督学习策略。网络的输出层神经元相互竞争,每个时刻仅有一个竞争获胜的神经元被激活,其他被抑制,即“胜者通吃”原则。
ART(Adaptive Resonance Theory,自适应谐振理论)网络是竞争性学习的代表。由比较层、识别层、识别阈值和重置模块构成。
流程:
- 比较曾接收输入样本,并传递给识别层。
- 识别层每个神经元对应一个模式类,神经元数目可在训练过程中动态增长以增加新的模式类(增量学习/在线学习)
- 识别层的神经元之间相互竞争:
- 计算输入向量与每个识别层神经元所对应的模式类的代表向量之间的距离,距离最小者胜。
- 若输入向量与获胜神经元所对应的代表向量之间的相似度大于识别阈值,则当前输入样本将被归为该代表向量所属类别。同时,网络连接权将会更新,使得以后在接收到相似输入样本时该模式类会计算出更大的相似度,从而使该获胜神经元有更大可能获胜
- 若相似度不大于识别阈值,则重置模块将在识别层增设一个新的神经元,其代表向量就设置为当前输入向量。
- 计算输入向量与每个识别层神经元所对应的模式类的代表向量之间的距离,距离最小者胜。
ART比较好地缓解了竞争型学习中的“可塑性稳定性窘境”(stability-plasticity dilemma),可塑性是指神经网络要有学习新知识的能力,而稳定性则是指神经网络在学习新知识时要保持对旧知识的记忆。这就使得ART网络具有一个很重要的优点:可进行增量学习(incremental learning)或在线学习(online learning)。
5.3 SOM网络
SOM(Self-Organizing Map,自组织映射)网络:竞争学习型的无监督神经网络。将高维输入数据映射到低维空间,同时保持输入数据在高维空间的拓扑结构,即将高维空间中相似的样本点映射到网络输出层中的临近神经元。
5.4 级联相关网络
结构自适应网络:不仅利用训练样本确定合适的连接权、阈值等参数,还将网络结构作为学习的目标之一。级联相关(Cascade-Correlation)网络是结构自适应网络的代表。
- 级联:建立层次连接的层级结构。
- 相关:通过最大化新神经元的输出与网络误差之间的相关性(correlation)来训练相关的参数。
优点:无需设置网络层数、隐层神经元数目,训练速度较快
缺点:数据较小时容易陷入过拟合。
5.5 Elman网络
递归神经网络(recurrent neural networks, RNN):允许网络中出现环形结构,从而可以让神经元的输出反馈回来作为输入信号。这样使得网络在 t t t时刻的状态不仅与 t t t时刻的输入有关,还与 t − 1 t-1 t−1时刻的网络状态有关,从而处理与时间有关的动态变化。
Elman网络是最常用的递归神经网络之一。隐层神经元的输出被反馈回来,与下一时刻的输入层神经元提供的信号一起,作为隐层神经元的输出在下一时刻的输入。隐层神经元常常采用Sigmoid激活函数,网络的训练常通过推广的BP算法进行。
5.6 Boltzmann机
Boltzmann机(平衡态分布) 是一种“基于能量的模型”(最小化能量,达到理想状态),其神经元分为两层:显层与隐层。显层用于表示数据的输入和输出,隐层是数据的内在表达。
6 深度学习
典型的深度学习模型就是很深层的神经网络。提高容量的一个简单办法是增加隐层的数目:隐层多了,相应的神经元连接权、阈值等参数就会更多。模型复杂度也可通过单纯增加隐层神经元的数目来实现。
单隐层的多层前馈网络已具有很强大的学习能力;但从增加模型复杂度的角度来看,增加隐层的数目显然比增加隐层神经元的数目更有效,因为增加隐层数不仅增加了拥有激活函数的神经元数目,还增加了激活函数嵌套的层数。然而,多隐层神经网络难以直接用经典算法(例如标准BP算法)进行训练,因为误差在多隐层内逆传播时,往往会“发散”(diverge)而不能收敛到稳定状态。
训练方法:
-
无监督逐层训练(unsupervised layer-wise training) 是多隐层网络训练的有效手段。其基本思想:
-
每次训练一层隐结点,训练时将上一层隐结点的输出作为输入,本层隐结点的输出作为下一层的输入,即“预训练”(pre-training)
-
与训练完成后,对整个网络进行微调(fine-tuning)训练
-
-
权共享: 让一组神经元采用相同的连接权。这个策略在卷积神经网络CNN中发挥了重要作用。
从另一个角度来理解深度学习。无论是DBN(深度信念网络)还是CNN(卷积神经网络),其多隐层堆叠、每层对上一层的输出进行处理的机制,可看作是在对输入信号进行逐层加工,从而把初始的、与输出目标之间联系不太密切的输入表示,转化成与输出目标联系更密切的表示,使得原来仅基于最后一层输出映射难以完成的任务成为可能。换言之,通过多层处理,逐渐将初始的**“低层”特征表示转化为“高层”特征表示后,用“简单模型”即可完成复杂的分类等学习任务。由此可将深度学习理解为进行“特征学习”(feature learning)或“表示学习”(representation learning).