支持多数不规则用户的隐私保护联邦学习框架

摘要

针对联邦学习存在处理大多数不规则用户易引起聚合效率降低，以及采用明文通信导致参数隐私泄露的问题，基于设计的安全除法协议构建针对不规则用户鲁棒的隐私保护联邦学习框架。该框架通过将模型相关计算外包给两台边缘服务器以减小采用同态加密产生的高额计算开销，不仅允许模型及其相关信息以密文形式在边缘服务器上进行密文聚合，还支持用户在本地进行模型可靠性计算以减小传统方法采用安全乘法协议造成的额外通信开销。在该框架的基础上，为更精准评估模型的泛化性能，用户完成本地模型参数更新后，利用边缘服务器下发的验证集与本地持有的验证集联合计算模型损失值，并结合损失值历史信息动态更新模型可靠性以作为模型权重。进一步，在模型可靠性先验知识指导下进行模型权重缩放，将密文模型与密文权重信息交由边缘服务器对全局模型参数进行聚合更新，保证全局模型变化主要由高质量数据用户贡献，提高收敛速度。通过HybridArgument模型进行安全性分析，论证表明PPRFL（privacy-preserving robust federated learning）可以有效保护模型参数以及包括用户可靠性等中间交互参数的隐私。实验结果表明，当联邦聚合任务中的所有参与方均为不规则用户时，PPRFL 方案准确率仍然能达到 92%，收敛效率较 PPFDL （privacy-preserving federated deep learning with irregular users）提高1.4倍；当联邦聚合任务中80%用户持有的训练数据都为噪声数据时，PPRFL方案准确率仍然能达到89%，收敛效率较PPFDL提高2.3倍。

关键词： 联邦学习 ; 隐私保护 ; 安全聚合 ; 大多数不规则用户 ; 安全除法协议

0 引言

近年来，各类数据驱动的深度学习（DL，deep learning）系统性能获得大幅提升，人工智能实现了经济与公众效益的共赢[1]。然而，由第三方服务商收集用户数据将不可避免地导致个人隐私数据泄露[2]。为解决数据孤岛难题并实现数据隐私共享，联邦学习（FL，federated learning）技术应运而生[3-4]。尽管联邦学习能缓解公众对隐私泄露的担忧，但相关研究[5-6]表明，攻击者可以通过用户上传的明文梯度信息间接推理出用户本地部分数据集成员和对应标签的信息。此外，明文梯度有可能遭受模型反演、模型推理等攻击[7]，导致数据隐私泄露。

针对联邦学习梯度逆推带来的新挑战，已有一些研究[8-9]聚焦于提升联邦学习的隐私性，并应用于各种场景[10,11,12]。在保证隐私性的同时，多种联邦学习方案进一步研究如何提高系统的训练效率。Kanagavelu等[13]为降低通信成本和提高可扩展性，提出一种支持安全多方计算的两阶段联邦学习方案。董业等[14]基于秘密共享技术和 Top-K梯度选择算法，提出高效安全的联邦学习框架。Aono 等[15]对梯度数据进行同态加密，保证多个训练者的本地数据隐私安全。文献[16]方案使用Paillier同态加密方法优化加密模型聚合过程。

然而，这些隐私保护联邦学习方案假设每个用户均持有高质量的数据，没有考虑系统中存在不规则用户的情况。实际上，拥有高级专业知识或高级设备的用户通常会生成高质量的数据，其他用户却可能由于噪声干扰、记录错误等产生低质量数据，这些用户称为不规则用户[17]，他们上传的模型参数可能会对全局模型精度造成负面影响。

隐私保护的深度学习协作系统（SecProbe，privacy-preserving collaborative deep learning system）[17]是第一种处理不规则用户的方案，该方案采用差分隐私技术向深度神经网络（DNN，deep neural network）添加噪声，并提出在线抽样选择用户的机制。已有研究[6,18]表明目前用于个性化深度学习的差分隐私机制，尚不能为复杂任务提供可接受的效用与隐私权衡。成艺等[19]集成Diffie-Hellman 密钥协商技术和 Shamir (t,n)门限机制[20]设计保护聚合结果的减少异质性数据影响的联邦学习方案（SAHPP，a privacy-preserving federated learning solution to reduce the impact of heterogeneous data）方案，该方案需要用户与其他多个用户进行密钥协商，消耗大量的网络资源，不适合大规模联合学习。Xu 等[21]基于真值发现方法[18,22]和边缘计算架构[22,23,24]设计在线计算模型梯度可靠性、存在不规则用户的隐私保护联邦深度学习（PPFDL，privacy-preserving federated deep learning with irregular users）方案。然而，SAHPP和PPFDL严重依赖于局部模型与中心聚合模型的距离，在不规则用户占大多数参与方的场景下，其聚合效率受到较大影响。

针对上述直接传输原始模型梯度导致模型隐私信息泄露以及大多数不规则用户存在导致现有联邦学习框架效率降低的严峻问题，本文提出一种支持大多数不规则用户鲁棒的隐私保护联邦学习（PPRFL，privacy-preserving robust federated learning）框架，主要贡献总结如下。

1）设计一种动态的模型可靠性更新策略，解决大多数不规则用户参与训练的精度提升缓慢问题，并基于可靠性先验知识指导模型权重缩放，实现全局模型聚合更新，保证全局模型变化主要由高质量数据用户贡献，进一步提高了联邦模型收敛的效率。

2）设计高效的安全除法协议，构建边缘服务器辅助的鲁棒隐私保护联邦学习框架PPRFL，规避上传和处理过程中的模型参数隐私泄露风险。

3）安全性详细证明PPRFL框架可以有效保护模型参数的隐私性。实验结果表明，当所有参与方都为不规则用户时，PPRFL方案的准确率仍可达92%，相比PPFDL方案，聚合效率提高1.4倍，并且服务器间的计算与通信开销较低。

1 预备知识

1.1 联邦学习

联邦学习框架一般由中心服务器和持有隐私数据的用户构成[25]，系统中的用户在接收初始模型后对本地参数进行训练。给定训练集D={(xi,yi);i=1,2,⋯,N}D={(xi,yi);i=1,2,⋯,N}和模型参数w，DNN的输出可表示为y= f(xi,w)，其中f为神经网络的输出函数，y为模型输出结果。参数训练的目的为从函数集合中寻找一个函数来近似每个样本特征向量xi到标签yi之间的真实映射关系。训练集上的目标损失函数如式(1)所示，lf(x,y,w)lf(x,y,w)为单个样本的损失，如交叉熵损失lf(x,y,w)=−ylnf(x,w)−(1−y)ln(1−f(x,w))lf(x,y,w)=−ylnf(x,w)−(1−y)ln(1−f(x,w))。交叉熵损失函数通常用于分类任务，本文实验采用该损失函数作为用户端的损失函数。

Lf(D,w)=1|D|∑〈x,y〉∈Dlf(x,y,w)　　　　(1)Lf(D,w)=1|D|∑〈x,y〉∈Dlf(x,y,w)　　　　(1)

在 j次训练时，采用随机梯度下降（SGD， stochastic gradient descent）方法更新模型参数，直到目标函数Lf(D,w)Lf(D,w)达到最小值，其中η为学习率，如式(2)所示。在联邦学习训练过程中，用户基于本地数据集使用 SGD 方法优化模型参数,并对同一批数据进行多次训练。

wj+1←wj−η1|D|∑n=1N∂Lf(D(n),wj)∂w　　　(2)wj+1←wj−η1|D|∑n=1N∂Lf(D(n),wj)∂w　　　(2)

为避免服务器访问本地数据，用户将训练后的模型发送给服务器。服务器收到用户i∈[1,n]发送的模型参数wj+1iwij+1和数据集数量 |Di||Di| 后，通常采用如式(3)进行全局模型更新[26]。

wj+1←wj−η∑i=1nwj+1i|Di|　　　　(3)wj+1←wj−η∑i=1nwij+1|Di|　　　　(3)

1.2 Paillier密码系统

Paillier 密码系统[27]是一种部分同态加密方案（PHE，partial homomorphic encryption），包含密钥生成、加密和解密算法，具有加法同态的性质[28]。已知明文消息m1和m2，使用同一公钥pk可加密为密文 Encpk(m1)Encpk(m1) 和Encpk(m2)Encpk(m2) ，满足Encpk(m1)⋅Encpk(m2)=Encpk(m1+m2)Encpk(m1)⋅Encpk(m2)=Encpk(m1+m2) 。已知常数t和明文消息m，满足Encpk(m) t=Encpk(t⋅m)Encpk(m) t=Encpk(t⋅m)。为避免明文模型与交互参数在通信和处理过程中的隐私泄露风险，本文利用Paillier 密码系统构建了边缘服务器辅助的隐私保护联邦学习框架。

2 系统模型与安全模型

2.1 系统模型

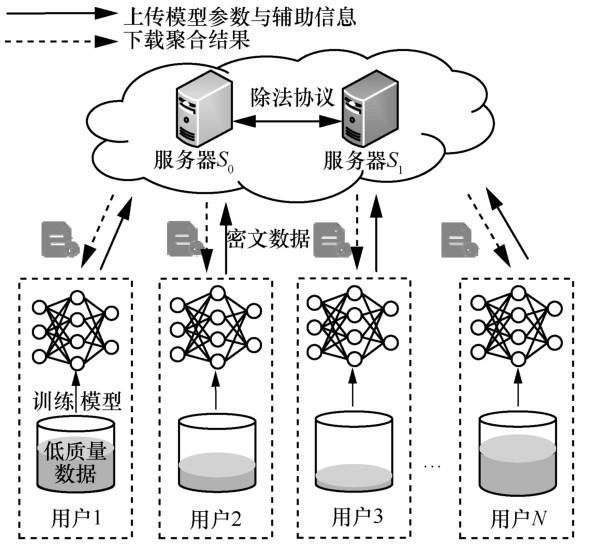
PPRFL框架的系统模型如图1所示，包含服务器端和用户端。用户首先利用本地数据集对模型进行更新，然后基于验证集损失值计算模型的可靠性，并将相关信息加密发送给服务器。两台非共谋的服务器S0和S1交互执行隐私保护模型聚合过程，并将加密全局模型返回给所有用户。服务器和用户反复执行这个流程，直到全局模型满足预定义的终止迭代条件。其中，S0作为接收用户加密数据的边缘服务器，S1提供解密密钥并协助S0进行计算。这种架构广泛地应用于外包计算场景[17,21-22]，其优点在于外包计算给两台边缘服务器以减轻本地计算资源的压力。

图1

图1   PPRFL方案系统模型Figure 1 System model of the PPRFL scheme

2.2 安全模型

如同大多数外包计算场景的安全假设一样，两台服务器为不共谋的诚实但好奇服务器[20-22]。服务器能正确地执行协议规范和相应操作，但可能利用在协议期间收集到的存储信息和消息流中的数据来推测用户的隐私数据[29]。恶意用户通常会对图像进行标签翻转或植入 Pattern 实现投毒攻击。与恶意用户不同，不规则用户通常在生成和存储数据的过程中，由于记录错误、噪声数据干扰、使用陈旧数据等产生低质量数据。此外，用户会诚实地执行模型训练以及后续加密上传等操作，因此认为用户是可信的。

此外，模型引入一个概率多项式时间的敌手AA，该敌手拥有下述攻击能力和约束。①AA可能攻击S1以猜测来自用户密文对应的明文值，也可能通过执行交互协议猜测来自另一方服务器密文对应的明文值。②AA可能攻击S2，通过执行交互协议猜测来自S1密文对应的明文值。③AA不能同时攻击S1和S2。若服务器和AA不能获得隐私信息，则意味着本文方案在此安全模型下是安全的。

基于上述威胁模型，与文献[19,21]类似，本文有如下隐私需求。① 用户模型参数。敌手可以通过本地模型和全局模型参数对用户进行成员推理等攻击恢复出用户的敏感信息，为保护用户数据隐私，模型参数应该以密文形式提交到服务器。② 模型可靠性。模型可靠性可以认为是用户数据质量的评价，为使学习过程公平无歧视，这个信息应对除用户外的其他参与方保密。③ 模型聚合结果。全局模型的聚合结果可以视为用户使用大量数据资源生成的知识产权，除了参与训练的用户外应对其他参与方保密。

3 PPRFL方案

PPRFL包含用户端和服务器端两个部分，用户端上的参与方在本地训练得到局部模型，基于组合验证集计算损失值，并结合历史信息，采用动态更新以及权重缩放方式得到模型可靠性；在服务器端上，服务器收到加密参数后先利用加同态性质进行聚合，然后交互执行安全除法协议得到全局模型。参与联邦学习的用户有着相似的收集数据场景，类似于隐私保护联邦学习方案[11,15,30]，本文考虑每个用户持有的高质量数据都满足独立同分布（IID，independent and identically distributed）。

3.1 模型可靠性更新

本节通过验证集损失分析来介绍处理大多数不规则用户的动态更新策略。在低质量数据集的联邦学习场景中，直接使用验证集损失值作为模型权重的计算方法将导致权重区分度失衡。这种失衡表现为经不同噪声比例数据训练出来的模型，在同一损失值下模型精度差异大；或是在相同的模型精度上，损失值差异大。基于以上观察，本文设计组合验证集计算用户模型损失值，并结合损失值历史信息辅助评估当前模型可靠性的动态更新方法。

具体来说，在第E轮迭代中，用户i结合本地验证集和服务器验证集共同计算损失值lossEilossiE。由于用户模型可能对本地数据拟合效果好，产生较低损失值的可能性较大，直接使用本地验证集损失值作为模型可靠性的计算依据是不公平的。而采用服务器维护的小部分高质量验证集[18,31-32]损失情况作为计算依据，将不能得到本地模型对噪声数据的拟合情况。

为了更精准地评估模型的泛化性能，采用本地验证集和服务器验证集共同计算损失，计算方法如式(4)所示，其中|Dv||Dv| 表示本地验证集数量， |Dt||Dt| 表示服务器验证集数量。

lossEi=lossiE=

|Dv||Dv|+|Dt|∑〈x,y〉∈Dvlf(x,y,w)+|Dt||Dv|+|Dt|∑〈x,y〉∈Dtlf(x,y,w)　　　(4)|Dv||Dv|+|Dt|∑〈x,y〉∈Dvlf(x,y,w)+|Dt||Dv|+|Dt|∑〈x,y〉∈Dtlf(x,y,w)　　　(4)

已有研究[33,34,35]表明历史行为可以反映一个实体在当下活动中的可靠程度。受此启发，本文考虑结合损失值的历史信息来动态更新当前用户模型的可靠性。在得到 lossEilossiE后，利用第E-1轮的模型可靠性uE−1iuiE−1，计算得到当前轮次的模型可靠性uEiuiE，如式(5)所示。

uEi=lossEi+γuE−1i　　　　(5)uiE=lossiE+γuiE−1　　　　(5)

其中，γ=12+lnE10γ=12+lnE10 ，γ随着E的增加而缓慢增加，并且当E=1时， uE−1i=0uiE−1=0。

此外，随着全局训练迭代轮次增加，用户模型损失值差异逐渐减小，不规则用户模型占全局模型权重逐渐提高。文献[18,22]表明不同用户利用高质量IID样本训练得到的梯度，在梯度下降方向上有着很高的相似概率，这些高质量IID数据产生的梯度更加接近于使全局损失最小化的最优梯度[19]。由于不规则用户采用噪声数据对模型进行训练，产生的梯度会偏离高质量数据产生的梯度方向。因此，大量不规则用户参与聚合将会减缓全局模型收敛速度。为解决上述问题，本文基于可靠性先验知识，采用式(6)方式对模型可靠性进行缩放。在固定训练轮次E下，将基于损失值的模型可靠性ui映射到函数上，使ui越小τi越大。随着训练轮次E的增加，激励小值ui对应的τi，抑制大值ui对应的τi。通过这样缩放可靠性的方式，减小不规则用户模型在全局模型的占比权重，保证全局梯度方向主要由高质量数据用户模型贡献。

τi=⎧⎩⎨(1ln2)uEi,E=1(1lnE)uEi,E≥2　　　　(6)τi={(1ln2)uiE,E=1(1lnE)uiE,E≥2　　　　(6)

PPRFL框架在用户端的执行算法如算法1所示，在用户i得到模型可靠性τi之后，结合模型参数 WiWi 计算 wˆi←wi⋅τiw^i←wi⋅τi，并将加密参数Encpk(wˆi)Encpk(w^i)和Encpk(τi)Encpk(τi) 上传到服务器S0。

算法1 PPRFL框架在用户端的执行算法

初始化 用户持有公-私钥对(pk,sk)

输入 用户持有 Encpk(w¯¯¯)Encpk(w¯)

输出 用户返回 Encpk(wˆi)Encpk(w^i) 和Encpk(τi)Encpk(τi)

1) 对于每一个用户i∈[1,n]

2) 从服务器端下载初始化加密模型，使用sk 解密得到模型参数w¯¯¯w¯

3) 在每一轮中执行 SGD，以式(2)方式更新模型参数WiWi

4) 以式(4)方式在组合验证集计算损失值lossEilossiE

5) 以式(5)方式计算模型可靠性uEi=lossEi+γuE−1iuiE=lossiE+γuiE−1

6) 以式(6)方式计算缩放后的模型可靠性τi

7) 采用wˆi←wi⋅τiw^i←wi⋅τi更新模型参数

8) 将 wˆiw^i 和τi 加密为 Encpk(wˆi)Encpk(w^i) 和Encpk(τi)Encpk(τi)，并上传到服务器S0

9) 进入下一轮迭代

3.2 模型聚合更新

本节介绍 PPRFL 框架在服务器端进行模型聚合更新的执行算法，具体步骤如下。

初始化 服务器S0持有公钥pk,服务器S1持有公-私钥对(pk,sk)

输入 用户发送 Encpk(wˆi)Encpk(w^i)、 Encpk(τi)Encpk(τi)到S0

输出 S 0返回 Encpk(w¯¯¯)Encpk(w¯)

1) S 0接收 Encpk(wˆi)Encpk(w^i)和 Encpk(τi)Encpk(τi)

2) 对于每一个i∈[1,n]

3) S 0计算Encpk(τ)←∏i=1nEncpk(τi)Encpk(τ)←∏i=1nEncpk(τi)

4) S 0计算Encpk(wˆ)←∏i=1nEncpk(wˆi)Encpk(w^)←∏i=1nEncpk(w^i)

5) S 1辅助S0执行安全除法协议，以式(7)方式计算密文下的全局模型参数Encpk(w¯¯¯)←Encpk(wˆτ)Encpk(w¯)←Encpk(w^τ)

6) S 0下发 Encpk(w¯¯¯)Encpk(w¯)给所有用户

7) 返回1)进入下一轮迭代

其中安全除法协议的构造详见附录。

S 0 首先聚合用户的加密模型可靠性Encpk(τi)Encpk(τi)和加密模型参数 Encpk(wˆi)Encpk(w^i)，进而得到含有权重的加密模型参数 Encpk(wˆ)Encpk(w^)。接下来，S0和S1协同执行安全除法协议得到归一化的加密全局模型参数 Encpk(w¯¯¯)Encpk(w¯) ，如式(7)所示。易见，某一用户的可靠性越高，该用户的模型参数在聚合后将占有越大的比例。最后，S0下发 Encpk(w¯¯¯)Encpk(w¯)给所有用户，用户可以使用sk解密得到全局模型参数w¯¯¯w¯。达到终止条件后，算法停止迭代。

w¯¯¯=∑i=1i=nτiwi∑i=1i=nτi　　　　(7)w¯=∑i=1i=nτiwi∑i=1i=nτi　　　　(7)

4 理论分析

4.1 安全性分析

命题 1 PPRFL 的安全性是服务器S0和S1无法获知任意用户的模型信息和协议交互过程中产生的明文结果。

证明 本文通过Hybrid Argument[8]模型来证明命题1。给定安全参数λ、n个用户以及两个非共谋服务器S0和S1，采用 δreal 表示 PPRFL 框架中S0和S1的真实视图。另外，证明存在一个概率多项式时间敌手AA，对于用户、S0和S1而言，AA的输出 δsim与δreal在计算上是不可区分的。

假设 1 初始化一个与真实视图δreal同分布的变量。

假设 2 在这个过程中，本文改变每个用户的行为，每个用户在Paillier密码系统下使用公钥pk1加密随机数ηaiηia而不是模型参数waiwia。S0和S1不共谋的假设以及 Paillier 密码系统的安全性可以确保假设2与假设1是不可区分的。

假设 3 模拟S0计算 Encpk(λ)←∏i=1nEncpk(λi)Encpk(λ)←∏i=1nEncpk(λi)和 Encpk(ηˆ)←∏i=1nEncpk(ηiˆ)Encpk(η^)←∏i=1nEncpk(ηi^) 而不是 Encpk(τ)←∏i=1nEncpk(τi)Encpk(τ)←∏i=1nEncpk(τi)和 Encpk(wˆ)←∏i=1nEncpk(wˆi)Encpk(w^)←∏i=1nEncpk(w^i) 。S0和S1不共谋的假设以及 Paillier 密码系统的安全性可以确保 δsim与δreal在计算上是不可区分的。因此，假设3与假设2是不可区分的。

假设 4 使用  Encpk(ηaˆ) Encpk(ηa^) 和Encpk(λ)Encpk(λ)而不是Encpk(τ)Encpk(τ) 和Encpk(wˆ)Encpk(w^) 作为安全除法协议的输入。由于附录的命题 2 证明了安全除法协议的安全性，可知S0和S1在计算上无法区分 δsim 与 δreal。因此，假设4与假设3也是不可区分的。

如上所示，利用Paillier密码系统和除法协议的安全性，可以得到概率多项式时间敌手AA的输出δsim，在计算上与 δreal不可区分。而该不可区分性保证S0和S1在这些交互中无法从 δsim 获得关于任何 δreal的信息。

证毕。

4.2 功能性分析

表1比较了SecProbe[17]、SAHPP[19]、PPFDL[21]以及本文PPRFL框架的功能性，4种方案均能保护用户上传的模型参数信息。运行在半可信服务器环境下的SecProbe需要在线评估模型效用并进行模型聚合，这会造成可靠性隐私和聚合模型参数隐私泄露的问题，并且SecProbe采用的差分隐私方法不支持用户中途退出。SAHPP、PPFDL以及本文方案采用同态加密体系，对中间过程参数和聚合结果都进行保护，服务器无法得知用户可靠性和聚合参数结果。此外，SecProbe、SAHPP和 PPFDL 在设计之初考虑的是低质量数据不超过全局总数据量一半的情况，在噪声数据占比过多时将造成聚合效率降低的问题。而本文的PPRFL框架依托组合验证集上的损失值，并采用动态更新和缩放方式计算模型可靠性，使本文方案在大多数不规则用户环境下仍能保持较高的模型收敛效率。

表1   不同方案的功能性比较Table 1 Comparison of functionality among different schemes

方案	保护模型参数	保护用户可靠性	保护聚合参数	用户退出鲁棒性	模型收敛效率
ecProbe[17]	√	×	×	×	×
SAHPP[19]	√	√	√	√	×
PPFDL[21]	√	√	√	√	×
PPRFL	√	√	√	√	√
注：“√”表示满足对应功能，“×”表示不满足。

5 性能分析

本节从模型收敛速度角度出发，详细分析实验结果以评估PPRFL框架的可应用性。实验采用Python环境并使用MNIST数据集[37]，该数据集包含55 000个训练集样本、5 000个验证集样本以及10 000个测试集样本。由于方案需要用到密码原语，使用Paillier库模拟同态加密过程，并利用 Matplotlib 数据绘图包输出实验结果。为生成用户数据，本文将 MNIST 训练集划分成等量的i份，对于用户i持有的数据集Di有 ∑|Di|=55 000∑|Di|=55 000。并且将MNIST验证集划分成等量的i+1份，其中服务器持有一份验证集。

实验设备配置如下：服务器以及可信第三方，由两台服务器模拟，其配置分别为 Intel Core i5-10400 CPU @ 2.90GHz 和 64 GB RAM， 512SSD、2TB机械硬盘；所有用户程序运行的设备配置为Intel Core i7-6700 CPU@ 3.40GHz。此外，类似于文献[19,21]方案，用户在本地上运行相同的卷积神经网络以获得训练后的模型参数，其中采用的卷积神经网络分别包含 20 个特征图和50 个特征图的两个5 × 5卷积层、一个平均池化层和分别包含256、10个神经元的完全连接层，每层使用ReLu 激活函数，并设置和前文工作[19,21]一致的学习速率0.01和选择的最小批量大小128。

在功能性分析中，SecProbe[17]会导致模型可靠性和聚合参数隐私泄露并且无法应对用户中途退出的情况。因此在接下来的分析中，本文只与安全性较强的SAHPP[19]和PPFDL[21]方案进行对比。

5.1 通信开销

根据2.1节系统模型的描述可知，用户与S0、S0与S1之间存在通信过程，会产生相应的通信开销。表2给出了3种方案在用户端与服务器端通信开销方面的对比，其中用户与S0之间的通信包括n个用户上传和下载容量为m的模型参数。

表2   不同方案的通信复杂度对比Table 2 Comparison of communication complexity among different schemes

方案	用户与第三方	用户与服务器S0	服务器S0与S1
SAHPP[19]	O(n)	O(n2+nm)	—
PPFDL[21]	—	O (nm)	O (κ(n+m))
PPRFL	—	O (nm)	O (m)

本文PPRFL在服务器端需要S0和S1进行m轮交互以计算安全除法协议，其通信复杂度为O(m)，这意味着服务器端的通信开销取决于模型参数数量，与用户数量无关。相比之下，PPFDL通信复杂度为O(κ(n+m))，与用户数量呈线性增长关系，其中κ为单轮聚合需要反复执行协议的次数。因此，本文PPRFL不仅适用于对通信能力有限的用户，并且服务器间的通信复杂度优于PPFDL。

5.2 计算开销

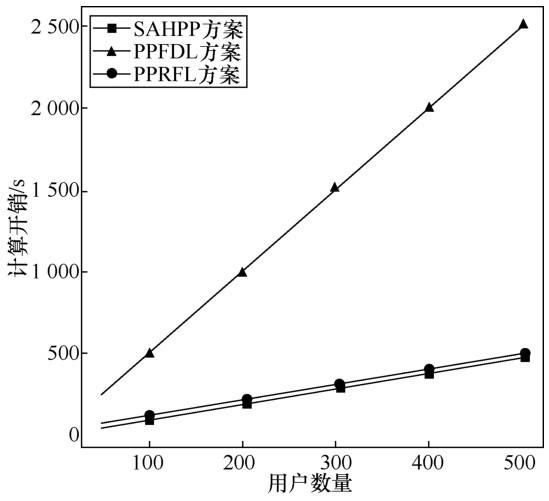
由于用户端的计算能力有限，在考虑模型精度和通信开销的同时应注意用户端的计算开销。图2给出在上传相同的模型参数数量时，不同方案的用户端计算开销。SAHPP[19]不仅需要密钥协商交互计算，并且需要计算本地模型与全局模型的空间距离，因此 SAHPP 方案中的用户端计算开销较高。PPFDL[21]仅需进行模型训练与模型参数加密，计算开销相比较低。PPRFL 比 PPFDL方案需要多执行一次前向计算和缩放模型参数计算，计算开销略高于PPFDL，但大大增强了模型对于不规则用户比例的鲁棒性。

本文 PPRFL 框架的计算开销主要由加密乘法和除法协议构成，计算复杂度为O(n+nm)。而PPFDL方案的计算开销主要由乘法协议构成，计算复杂度为O(2κnm)。如图3所示，在上传相同数量的梯度后，PPFDL方案的服务器端计算开销远高于PPRFL。SAHPP计算开销由计算复杂度为O(nm)的加密乘法构成，因此PPRFL与SAHPP的服务器端计算开销接近。但 PPFDL 在后续中引入安全传输技术（STT，secure transformation technique）[36]，使其计算复杂度降低为O(2κ(n+m))。为进一步比较计算开销，本文将 STT 引入PPRFL，使PPRFL计算复杂度降低到O(n+m)。如表3 所示，PPRFL 的计算复杂度相比 PPFDL较低。

图2

 

图2   不同方案的用户端计算开销Figure 2 Comparison of client’s computation costs among different schemes

 

图3

图3   不同方案的服务器端计算开销Figure 3 Comparison of server’s computation costs among different schemes

表3   不同方案的计算复杂度对比Table 3 Comparison of computational complexity among different schemes

方案	采用STT前	采用STT后
SAHPP[19]	O (nm)
PPFDL[21]	O (2κnm)	O (2κ(n+m))
PPRFL	O (n+nm)	O (n+m)

 

5.3 收敛效率

影响模型收敛效率的因素包括不规则用户比例和不规则用户持有数据的噪声比例以及参与的用户数量。为模拟该场景，本文设置系统中不规则用户的比例为P1，其中P1∈[0,1]。不规则用户持有的随机噪声数据量占本地总数据量的比例为P2（P2∈[0,1]）。在P1⋅P2≤50%时，SAHPP[19]和PPFDL[21]均能有效处理不规则用户模型，但在P1⋅P2≥50%情况下，过多不规则用户将使这些方案的聚合效率大大降低。而本文提出的可靠性动态更新以及权重缩放方法，可以有效应对P1⋅P2≥50%的情况。此外，本文设置的收敛效率计算方式如式(8)所示，其中Eff 为收敛效率， EpochPPFDL和 EpochPPRFL分别为 PPFDL 和PPRFL收敛到预设准确度需要的通信轮数。

Eff= EpochPPFDL EpochPPRFL　　　　(8)Eff= EpochPPFDL EpochPPRFL　　　　(8)

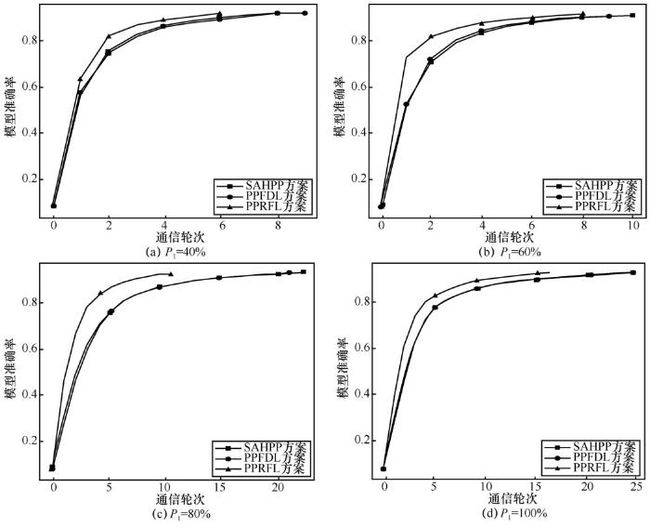
图4给出P2=80%、不同不规则用户比例P1， 3 种方案收敛效率的变化情况。可以观察到，系统中持有高质量数据的用户越多，全局模型的准确率就越高，达到收敛需要的轮次也越低。在图5(c)所示P1⋅P2=64%时，SAHPP、PPFDL和PPRFL方案收敛到准确率0.92需要的通信轮次分别为22、21和10，PPRFL收敛效率较PPRFL提高2倍。这是由于 PPRFL 能在众多不规则用户模型中识别出精度较高的模型，赋予其更高的权重保证聚合结果主要来源于这些模型，从而加快收敛速度。

当全局用户都为不规则用户时，所有模型准确率较低，各个方案达到收敛需要的轮次更多。如图4(d)所示P1=100%时，SAHPP、PPFDL 和PPRFL 方案收敛到预设准确率需要的通信轮次分别为25、25和17，PPRFL收敛效率较PPRFL提高1.4倍。基于中心梯度距离计算的SAHPP、PPFDL无法识别出哪些模型具有相对较好的效果，方案效率降低。PPRFL则能在这些低质量模型中提高相对优质模型的影响力，减少需要的收敛轮次。

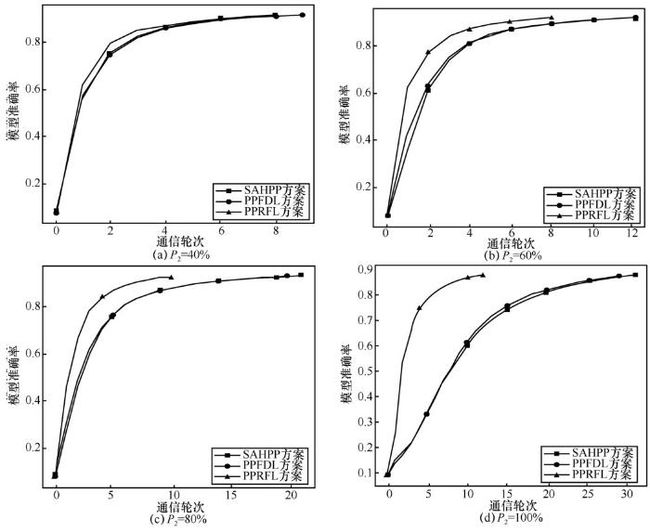
图5给出在相同P1（P1=80%）、不同P2值时，3种方案的模型精度随着迭代次数变化曲线。随着用户持有数据的噪声比P2的提高，全局模型收敛需要的轮次更多。在图5(d)全局总噪声数据占比达P1⋅P2=80%的情况下，SAHPP、PPFDL和PPRFL方案收敛到准确率0.89需要的轮次分别为32、30和13，PPRFL收敛效率较PPRFL提高2.3倍。该场景只有少量的用户持有高质量数据，PPRFL通过利用损失值历史信息更新可靠性和可靠性权重缩放等方法识别出这类用户，给予这些用户更多权值计数，大大提高前几轮聚合的模型准确率，达到更高的收敛效率。

图4

图4   不同用户比例下模型准确率随着通信轮次的变化曲线Figure 4 Curves showing the variations of model accuracy with number of communication rounds under different client ratios

 

图5

 

图5   不同噪声比例下模型准确率随着通信轮次的变化曲线Figure 5 Curves showing the variations of model accuracy with number of communication rounds under different noise ratios

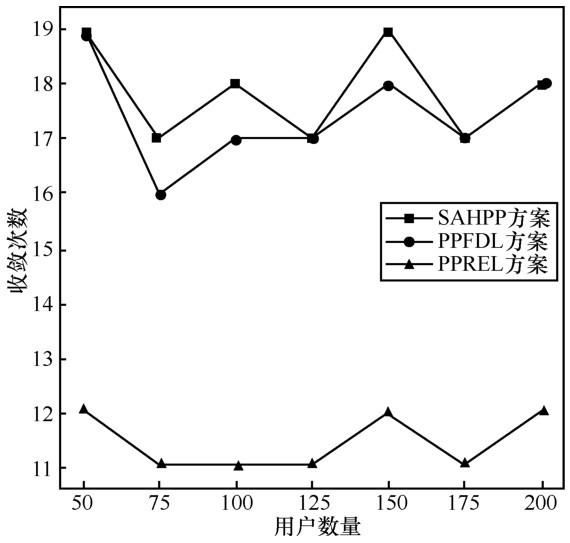
通常来说，参与联邦聚合的用户越多，模型的收敛速度和准确度将越高。但在该环境下，不规则用户随着参与的用户增加而增多，全局模型收敛速度受影响，收敛速度变化不规律。如图6 所示，在相同P1、P2时达到收敛准确率0.92，PPRFL较SAHPP、PPFDL 需要的收敛轮次少。这是由于在SAHPP和 PPFDL中，中心梯度受不规则用户影响，高质量数据的用户梯度与平均梯度空间距离远，这类用户模型权重占比减小，收敛效率降低。而PPRFL则考虑到更多不规则用户的“质量分数”，在一定限度上使聚合结果倾向于高质量数据的用户产生的模型。

图6

 

图6   相同噪声比下收敛次数随着用户数量的变化曲线Figure 6 Curves showing the variations of convergence counts with number of clients under the same noise ratios

 

6 结束语

针对现有联邦学习方案受大多数不规则用户影响产生聚合效率降低、采用明文通信导致隐私信息泄露的问题，本文提出了一种支持多数不规则用户的鲁棒隐私保护联邦学习框架 PPRFL。PPRFL在用户端利用组合验证集的损失值动态计算和缩放模型可靠性；在服务器端结合设计的除法协议进行安全参数聚合。经过理论分析和实验验证，PPRFL可以保证模型精度并提高联邦聚合的收敛效率，而且计算和通信开销均优于PPFDL。未来的工作将研究纵向联邦学习架构下处理不规则用户的方案，寻找进一步减小计算和通信开销的方法。

附录

本节详细介绍基于 PHE 的安全两方除法协议细节。PPFDL[21]提出了一种由两台不共谋服务器协作执行的安全除法协议SecDiv，但混淆电路以及不经意传输进行通信需要大量额外的计算开销。为了克服这一局限性，本文提出一种更加高效的安全除法协议，可信第三方为S1生成 PHE 的公私钥对(pk,sk)，并广播pk给S0，由S0和S1协作完成加密除法运算，具体构造如下。

输入 S 0持有密文Encpk(x)Encpk(x)、Encpk(y)Encpk(y)和公钥pk；S1持有公-私钥对(pk,sk)

输出 S 0返回密文Encpk(x/y)Encpk(x/y)

1) S 0随机选择h1和h2

2) S 0计算c0←Encpk(x) h1c0←Encpk(x) h1和c1←Encpk(y) h2c1←Encpk(y) h2，并发送c0和c1给S1

3) S 1 计 算 d0←Decsk(c0)d0←Decsk(c0)、d1←Decsk(c1)d1←Decsk(c1) 和c2←Encpk(d0/d1)c2←Encpk(d0/d1) ,并发送c2给S0

4) S 0计算Encpk(x/y)←ch2/h12Encpk(x/y)←c2h2/h1

安全除法协议的安全性证明如命题2所述。

命题2 基于PHE的安全除法协议中，S0和S1均无法获取明文值x、y和x/y。

证明 协议安全性依赖于 PHE 的安全性，S0仅知道密文Encpk(x)Encpk(x) 、Encpk(y)Encpk(y) 和Encpk(x/y)Encpk(x/y) ，不知道私钥sk，无法解密恢复出明文值x、y和x/y。依赖于随机独立分布的计算安全，S1仅知道h1⋅x、h2⋅y和h1⋅x/h2⋅y，无法获取h1和h2，不能推测出x、y和x/y。

证毕。

本文安全除法协议与 SecDiv 协议[21]的计算开销对比如表4 所示。记 SecDiv 构造混淆电路的计算时间为TOT、运行不经意传输的计算时间为TGC，一次密文乘密文计算时间记为 CMult ，一次明文乘密文计算时间记为Mult ，一次加密计算时间记为 Enc ，一次解密计算时间记为 Dec 。本文提出的安全除法协议仅比SecDiv多进行一次明文乘法而不需要执行开销更高的TOT和TGC。

表4   不同除法协议的计算开销对比Table 4 Comparison of computational overhead among different protocol

协议	TOT	TGC	CMult	Mult	Enc	Dec
SecDiv[21]	1	1	3	—	4	2
本文协议	—	—	3	1	3	2

在通信开销方面，SecDiv 需要 2 次通信传输同态密文，且需要执行通信开销较高的混淆电路和不经意传输操作，而本文提出的安全除法协议仅需要2次通信传输同态密文，通信开销远低于SecDiv协议。