UVa 10316 - Airline Hub

题目：给出地球上的n个机场的经度和纬度，想在这里面确定一个HUB使得他到其他机场的最大距离最小。

分析：计算几何、大地坐标系。因为数据不大直接枚举即可，比较时利用圆心角可以提高计算效率，并控制精度。

            利用公式可直接解得两点的空间圆心角：acos(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2))；

            因为又是大地坐标，所以再推一遍吧，推导过程如下：

                      

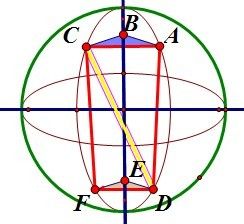
            如图，C，D为已知两点则有如下推导：            

            AB = r*cos(lat1)；DE = r*cos(lat2)；BE = r*sin(lat1) + r*sin(lat2)；

            AD*AD = BE*BE + (AB-DE)*(AB-DE) = 2*r*r - 2*r*r*sin(lat1)*sin(lat2) - 2*r*r*cos(lat1)*cos(lat2)；

            AC*AC = 2*AB*AB - 2*AB*AB*cos(lon1-lon2) = 2*r*r*cos(lat1)*cos(lat1)*(1-cos(lon1-lon2))；

            DF*DF = 2*DE*DE - 2*DE*DE*cos(lon1-lon2) = 2*r*r*cos(lat2)*cos(lat2)*(1-cos(lon1-lon2))；

            AC*DF = 2*r*r*cos(lat1)*cos(lat2)*(1-cos(lon1-lon2))；

            由托勒密定理有 AC*DF + AD*AD = CD*CD 整理有：

            CD = r*sqrt(2-2*(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2)))；

            设圆心角为α则：

            cos(0.5*α) = 0.5*CD/r = sqrt(0.5-0.5*(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2)))；

            cos(0.5*α)*cos(0.5*α) = 0.5 - 0.5*(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2))；

            cosα = 1 - 2*cos(0.5*α)*cos(0.5*α) = cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2)；

            圆心角为：acos(cos(lat1)*cos(lat2)*cos(lon1-lon2)+sin(lat1)*sin(lat2))；

注意：精度控制。

 

#include <iostream>

#include <cstdlib>

#include <cstdio>

#include <cmath>



using namespace std;



double dis[1005][1005];

double lat[1005];

double lon[1005];



double dist( double l1, double d1, double l2, double d2 )

{

	double p = acos(-1.0);

	l1 *= p/180.0; d1 *= p/180.0; 

	l2 *= p/180.0; d2 *= p/180.0; 

	return acos(cos(l1)*cos(l2)*cos(d1-d2)+sin(l1)*sin(l2));

}



int main()

{

	int n;

	while ( ~scanf("%d",&n) ) {

		for ( int i = 0 ; i < n ; ++ i )

			scanf("%lf%lf",&lat[i],&lon[i]);

		

		for ( int i = 0 ; i < n ; ++ i )

		for ( int j = i ; j < n ; ++ j )

			dis[i][j] = dis[j][i] = dist( lat[i], lon[i], lat[j], lon[j] );

		

		double min = 1e20;

		int    spa = 0;

		for ( int i = 0 ; i < n ; ++ i ) {

			double max = 0.0;

			for ( int j = 0 ; j < n ; ++ j )

				if ( max+1e-6 < dis[i][j] )

					max = dis[i][j];

			if ( min+1e-6 > max ) {

				min = max;

				spa = i;

			}

		}

		

		printf("%.2lf %.2lf\n",lat[spa],lon[spa]);

	}

	return 0;

}