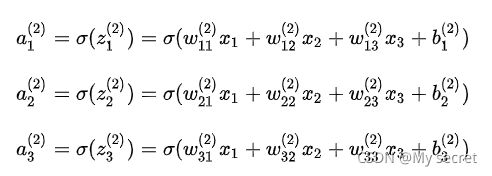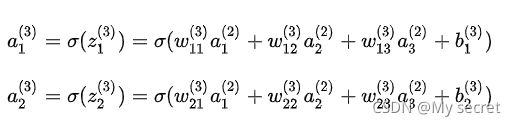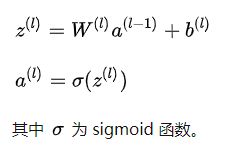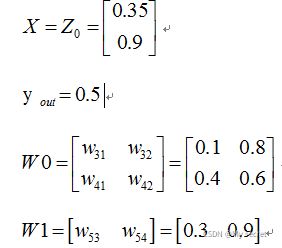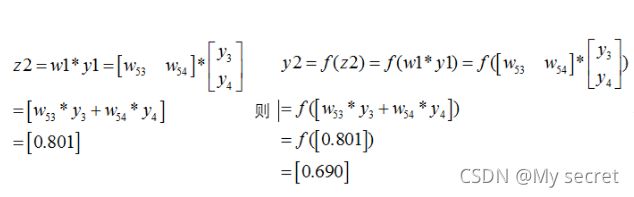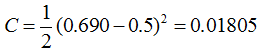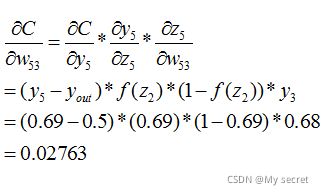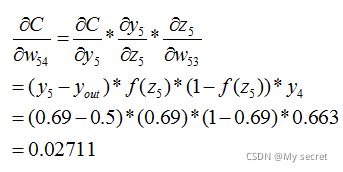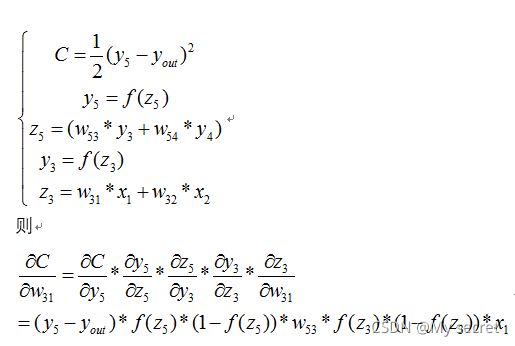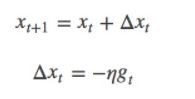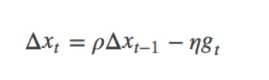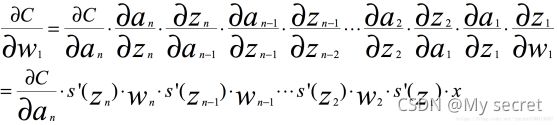机器学习二------前向传播过程 反向传播算法（BP算法）Dropout 梯度消失和梯度爆炸

1.前向传播过程 

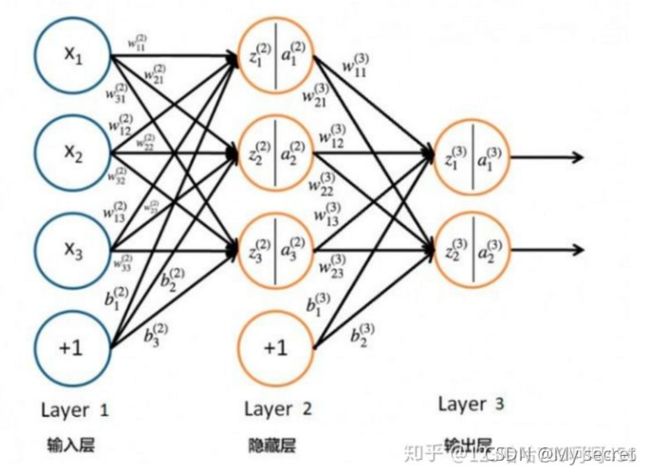
   思想：将上一层的输出作为下一层的输入，并计算下一层的输出，一直到运算到输出层为止。

 

 对于Layer 2的输出 

 对于Layer 3的输出，

 

 简化后的形式就是：

2.反向传播算法（BP算法）

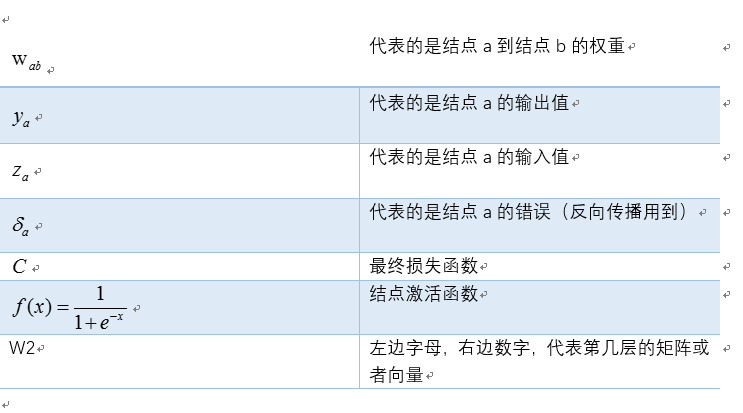
符号说明：

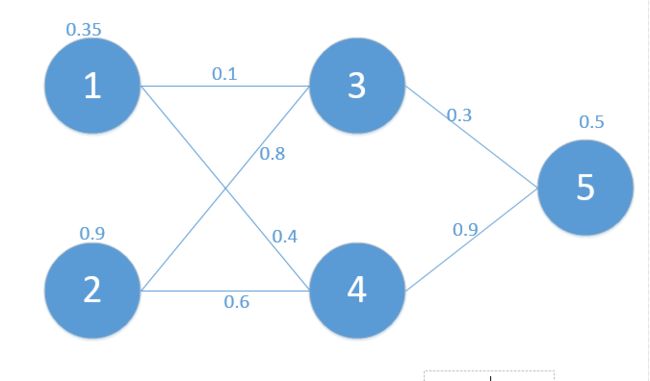
对应网络如下：

其中对应的矩阵表示如下：

正向传播计算过程：

 

同理：

所以最终的损失为：

接着推导反向传播，根据公式我们知道：

 

 我们需要求出C对w的偏导，则根据链式法则有：

 

同理也有：

同理如下：

 最终的结果为：

3.深度学习中常用的优化算(SGD,Nesterov,Adagrad,RMSProp,Adam)总结

SGD指stochastic gradient descent，即随机梯度下降。是梯度下降的batch版本。

对于训练数据集，我们首先将其分成n个batch，每个batch包含m个样本。我们每次更新都利用一个batch的数据，而非整个训练集。即：

                                     

其中，η为学习率，gt为x在t时刻的梯度。 

这么做的好处在于：

当训练数据太多时，利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力，并且可以更快地收敛。

当训练集有很多冗余时（类似的样本出现多次），batch方法收敛更快。以一个极端情况为例，若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch，后一半作为另一个batch，那么在一次遍历训练集时，batch的方法向最优解前进两个step，而整体的方法只前进一个step

Momentum

SGD方法的一个缺点是，其更新方向完全依赖于当前的batch，因而其更新十分不稳定。解决这一问题的一个简单的做法便是引入momentum。

momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力：

其中，ρ 即momentum，表示要在多大程度上保留原来的更新方向，这个值在0-1之间，在训练开始时，由于梯度可能会很大，所以初始值一般选为0.5；当梯度不那么大时，改为0.9。η 是学习率，即当前batch的梯度多大程度上影响最终更新方向，跟普通的SGD含义相同。ρ 与 η 之和不一定为1。

4.Dropout

过拟合的现象：模型训练数据上损失函数较小，预测准确率较高；但是在测试数据上损失函数比较大，预测准确率较低。

Dropout工作原理：在前向传播的时候，让某个神经元的激活值以一定的概率p停止工作，这样可以使模型泛化性更强，因为它不会太依赖某些局部的特征。

Dropout工作流程：

（1））首先随机（临时）删掉网络中一半的隐藏神经元，输入输出神经元保持不变（下图中虚线为部分临时被删除的神经元）

 （2） 然后把输入x通过修改后的网络前向传播，然后把得到的损失结果通过修改的网络反向传播。一小批训练样本执行完这个过程后，在没有被删除的神经元上按照随机梯度下降法更新对应的参数（w，b）

（3）然后继续重复这一过程：

. 恢复被删掉的神经元（此时被删除的神经元保持原样，而没有被删除的神经元已经有所更新）
. 从隐藏层神经元中随机选择一个一半大小的子集临时删除掉（备份被删除神经元的参数）。
. 对一小批训练样本，先前向传播然后反向传播损失并根据随机梯度下降法更新参数（w，b） （没有被删除的那一部分参数得到更新，删除的神经元参数保持被删除前的结果）。

不断重复1，2，3步骤

Dropout在神经网络中的使用：

在训练模型阶段：在训练网络的每个单元都要添加一道概率流程：

 对应的公式变化如下：

没有Dropout的网络计算公式：

采用Dropout的网络计算公式：

上面公式中Bernoulli函数是为了生成概率r向量，也就是随机生成一个0、1的向量。

代码层面实现让某个神经元以概率p停止工作，其实就是让它的激活函数值以概率p变为0。比如我们某一层网络神经元的个数为1000个，其激活函数输出值为y1、y2、y3、......、y1000，我们dropout比率选择0.4，那么这一层神经元经过dropout后，1000个神经元中会有大约400个的值被置为0。

注意： 经过上面屏蔽掉某些神经元，使其激活值为0以后，我们还需要对向量y1……y1000进行缩放，也就是乘以1/(1-p)。如果你在训练的时候，经过置0后，没有对y1……y1000进行缩放（rescale），那么在测试的时候，就需要对权重进行缩放，操作如下。

（2）在测试模型阶段

预测模型的时候，每一个神经单元的权重参数要乘以概率p。

测试阶段Dropout公式：

 为什么Dropout可以解决过拟合：

（1）取平均的作用： 先回到标准的模型即没有dropout，我们用相同的训练数据去训练5个不同的神经网络，一般会得到5个不同的结果，此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9，其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合，取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络，随机删掉一半隐藏神经元导致网络结构已经不同，整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。

（2）减少神经元之间复杂的共适应关系： 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ，这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测，它不应该对一些特定的线索片段太过敏感，即使丢失特定的线索，它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1，L2正则，减少权重使得网络对丢失特定神经元连接的鲁棒性提高。

（3）Dropout类似于性别在生物进化中的角色：物种为了生存往往会倾向于适应这种环境，环境突变则会导致物种难以做出及时反应，性别的出现可以繁衍出适应新环境的变种，有效的阻止过拟合，即避免环境改变时物种可能面临的灭绝。

5.归一化：

数据归一化的目的就是为了把不同来源的数据统一到同一数量级（一个参考坐标系）下，这样使得比较起来有意义。归一化使得后面数据的处理更为方便，它有两大优点：

（1）归一化可以加快梯度下降求最优解的速度

如下图，蓝色的圈圈表示特征的等高线。其中左图的两个特征x1和x2区间相差较大，x1~[0,2000],x2~[1,5],期所形成的等高线在一些区域相距非常远，当使用梯度下降法求解最优解的时候，很可能垂直等高线走“之字型”路线（左图红色路径），从而导致需要迭代很多次才能收敛，也可能不收敛。而右图对两个原始特征进行了归一化处理，其对应的等高线显得很圆，在梯度下降的时候就能很快收敛。因此，如果机器学习使用梯度下降法求解最优解时，归一化往往是非常有必要的。

（2）归一化有可能提高精度

一些分类器（如KNN）需要计算样本之间的距离（如欧式距离）。如果一个特征值域范围非常大，那么距离计算就要取决于这个特征，如果这时实际情况是值域范围小的特征更重要，那么归一化就要起作用了

归一化的方法：

（1）线性归一化：也称min-max标准化、离差标准化；是对原始数据的线性变换，使得结果值映射到[0,1]之间。转换函数如下：

 这种归一化比较适用在数值较集中的情况。这种方法有一个缺陷，就是如果max和min不稳定的时候，很容易使得归一化的结果不稳定，影响后续使用效果。其实在实际应用中，我们一般用经验常量来替代max和min。

（2）标准差归一化，也叫Z-score标准化，这种方法给予原始数据的均值（mean，μ）和标准差（standard deviation，σ）进行数据的标准化。经过处理后的数据符合标准正态分布，即均值为0，标准差为1，转化函数为：

 （3）非线性归一化，这种方法一般使用在数据分析比较大的场景，有些数值很大，有些很小，通过一些数学函数，将原始值进行映射。一般使用的函数包括log、指数、正切等，需要根据数据分布的具体情况来决定非线性函数的曲线。

6.深度学习中的难样例挖掘

（1）困难样本产生的原因：

     对于物体检测问题而言，检测器面对的是整个世界的物体，这些物体里面只有非常少的被标记了具体类别，大量的物体其实并没有类别信息，甚至根本不知道如何标记他的类别，所以面对开集问题，我们要求检测(分类)器要有非常好的排他能力或排除背景类别能力，那么训练数据将会非常重要，为了有这样的能力我们需要切割下大量的背景作为负样本(negative samples)来训练，但是这些背景样本是否足够了？不管加了多少背景数据，目前都无法从理论上回答这个问题：背景是否足够。 而事实上不管如果加背景数据训练，模型总能遇到不能正确分类或很难分类的背景样本（false positive) ，这个就是我们常说的困难负样本(hard negative samples) 与之相反的是 hard positive samples，统称为困难样本(hard samples)

（2）困难样本的挖掘方法：

     数据集：对于目标检测中我们会事先标记处ground truth，然后再算法中会生成一系列proposals，proposals与ground truth的IOU超过一定阈值（通常0.5）的则认定为是正样本，低于一定阈值的则是负样本，然后扔进网络中训练。However，这也许会出现一个问题那就是正样本的数量远远小于负样本，这样训练出来的分类器的效果总是有限的，会出现许多false positive，把其中得分较高的这些false positive当做所谓的Hard negative，既然mining出了这些Hard negative，就把这些扔进网络再训练一次，从而加强分类器判别假阳性的能力。

    loss上选取：选取与label差别大(loss大)的作为hard negtive

7.梯度消失和梯度爆炸：

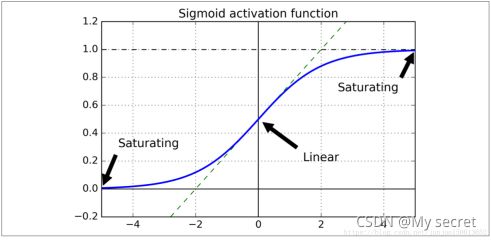
当神经网络有很多层，每个隐藏层都使用Sigmoid函数作为激励函数时，很容易引起梯度消失的问题，我们知道Sigmoid函数有一个缺点：当x较大或较小时，导数接近0；并且Sigmoid函数导数的最大值是0.25

 

我们将问题简单化来说明梯度消失问题，假设输入只有一个特征，没有偏置单元，每层只有一个神经元：

 

我们先进行前向传播,这里将Sigmoid激励函数写为s(x)：

z1 = w1*x

a1 = s(z1)

z2 = w2*a1

a2 = s(z2)

...

zn = wn*an-1 (这里n-1是下标)

an = s(zn)

根据链式求导和反向传播，我们很容易得出，其中C是代价函数

 

如果我们使用标准方法来初始化网络中的权重，那么会使用一个均值为0标准差为1的高斯分布。因此所有的权重通常会满足|wj|<1，而s‘是小于0.25的值，那么当神经网络特别深的时候，梯度呈指数级衰减，导数在每一层至少会被压缩为原来的1/4，当z值绝对值特别大时，导数趋于0，正是因为这两个原因，从输出层不断向输入层反向传播训练时，导数很容易逐渐变为0，使得权重和偏差参数无法被更新，导致神经网络无法被优化，训练永远不会收敛到良好的解决方案， 这被称为梯度消失问题。

梯度爆炸的原因：

当我们将w初始化为一个较大的值时，例如>10的值，那么从输出层到输入层每一层都会有一个s‘(zn)*wn的增倍，当s‘(zn)为0.25时s‘(zn)*wn>2.5，同梯度消失类似，当神经网络很深时，梯度呈指数级增长，最后到输入时，梯度将会非常大，我们会得到一个非常大的权重更新，这就是梯度爆炸的问题，在循环神经网络中最为常见.