TASK04|分类分析
目录
- 分类分析
-
- 分类问题与对应的模型
-
- 二分类问题
-
- 1.1 线性回归模型是如何处理分类问题的
- 两种映射函数——Logistic函数与Probit函数
-
- logistic函数
- Probit函数
- logistic线性回归函数
-
- Probit线性回归模型
- 模型推断
- 分类预测
-
- 1.5.1 模型预测的原理
- 1.5.2 预测结果呈现——混淆矩阵与多指标
-
- 混淆矩阵
-
-
- “样本不均衡”
-
- 1.5.3 对抗不平衡数据集——改变阈值
- 2. 无序多分类问题
-
-
- 多分类logistic的回归预测
- 2.1 多分类Logistic回归的两种算法
- 2.1.1 算法1:修改概率映射函数
- 2.1.2 算法2:一对其余算法
-
- 3. 以预测为目的分类问题实操流程——基于sklearn
-
- 3.1 划分训练集/测试集
- 3.2 训练模型/模型预测
- 3.3 预测结果分析
分类分析
回归和分类是数据分析的两大重要任务
回归分析的因变量是连续变量;
分类分析的因变量是分类属性变量
在进行分类分析之前,我们必须要弄清楚我们建模的目的是推断还是预测
以推断/分析为主,那么我们在建模时所采用的模型最好是易于解释的白盒模型,如一众线性模型
以预测为主,则我们建模的依据主要是预测的精度,模型的可解释性相对而言不那么重要
对于分类任务而言,当前预测精度高的模型基本上都是深度学习/机器学习模型(如:支持向量机、随机森林、Xgboost等),而这些模型的可解释性一般都很差
如果我们追求分类模型的可解释性,探究各自变量对分类决策的影响,那么使用线性模型框架下的分类模型就比较合适了(如:Logistic回归、Probit回归等)。
分类问题与对应的模型
分类问题按照被分类对象的类别划分,总共可以分为三类:二分类问题、无序多分类问题、有序多分类问题。
二分类问题:二分类Logistic回归模型与Probit模型
无序多分类问题(二分类问题的延伸):多类别logistic回归模型建模
有序多分类问题:有序Logistic回归
二分类问题
1.1 线性回归模型是如何处理分类问题的
· Example12. ST是我国股市特有的一项保护投资者利于的决策,当上市公司因财务状况不佳导致投资者难以预测其前景时,交易所会标记该公司股票为ST,并进行一系列限制措施。而在这项任务中,因变量就是公司是否会被ST,数学表示为:
y = { 1 , S T 0 , Otherwise y= \begin{cases}1, & S T \\ 0, & \text { Otherwise }\end{cases} y={1,0,ST Otherwise
在回归问题中,对于一个待预测样本 x x x,模型输出值 y ^ \hat{y} y^的性质就是因变量的性质
概率!准确来说是在给定 x x x下, y = 1 y=1 y=1的概率
P ( y = 1 ∣ x ) P(y=1 \mid x) P(y=1∣x)
· 概率的映射
与回归问题因变量天然确定的情况不一样,分类问题中概率的形式是需要我们人为确定的,即我们要确定如何将线性模型的直接输出值 y y y映射成概率值 P ( y = 1 ∣ x ) P(y=1 \mid x) P(y=1∣x)。
我们可以看到多元线性模型
y = β 0 + β 1 x 1 + ⋯ + β k x k + u y=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k}+u y=β0+β1x1+⋯+βkxk+u
的输出值 y y y是一个连续变量,而概率也是一个连续的变量,那么我们能不能让这个输出值 y = P ( y = 1 ∣ x ) y=P(y=1 \mid x) y=P(y=1∣x)呢?即有
P ( y = 1 ∣ x ) = y = β 0 + β 1 x 1 + ⋯ + β k x k + u P(y=1\mid x)=y=\beta _0+\beta _1x_1+\cdots +\beta _kx_k+u P(y=1∣x)=y=β0+β1x1+⋯+βkxk+u
这样做有一个最大的缺点—— y ^ \hat{y} y^可能不在区间(0,1)内,而概率只能在(0,1)区间内。(当然,还有其他的缺点,但大家只需要记住这个就可以了)
两种映射函数——Logistic函数与Probit函数
logistic函数
若映射函数为Logistic函数
G ( y ) = 1 1 + e − y G(y)=\frac{1}{1+e^{-y}} G(y)=1+e−y1
则整个预测模型被称为Logistic线性回归模型
Probit函数
若映射函数为Probit函数
Φ ( y ) = P ( Y ≤ y ) = ∫ − ∞ y 1 2 π exp ( − 1 2 x 2 ) d x \Phi(y)=P(Y \leq y)=\int_{-\infty}^{y} \frac{1}{\sqrt{2 \pi}} \exp \left(-\frac{1}{2} x^{2}\right) d x Φ(y)=P(Y≤y)=∫−∞y2π1exp(−21x2)dx
则整个预测模型被称为Probit线性回归模型。注意到,Probit函数实际上就是标准正态分布的累积函数。
logistic线性回归函数
记 y = x ′ β = β 0 + β 1 x 1 + ⋯ + β k x k y=x^{\prime} \beta=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k} y=x′β=β0+β1x1+⋯+βkxk,则Logistic回归模型形式为
P ( y = 1 ∣ x ) = p ( x ) = 1 1 + e − y = 1 1 + e − x ′ β P(y=1 \mid x)=p\left( x \right) =\frac{1}{1+e^{-y}}=\frac{1}{1+e^{-x^{'}\beta}} P(y=1∣x)=p(x)=1+e−y1=1+e−x′β1
log ( p ( x ) 1 − p ( x ) ) = β 0 + β 1 x 1 + ⋯ + β k x k \log \left(\frac{p(x)}{1-p(x)}\right)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k} log(1−p(x)p(x))=β0+β1x1+⋯+βkxk
Logistic回归模型与一般多元回归模型的一大区别在于,前者的因变量是一个有关概率 p ( y = 1 ∣ x ) p\left( y=1|x \right) p(y=1∣x)的函数,而后者的因变量只是其本身。
胜率(odd)=成功/失败
当其他自变量不变时,变量 x i x_i xi提升一个单位,胜率odd会提升 β j % \beta_j \% βj%
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy import stats
st_logit=sm.formula.logit('ST~ARA+ASSET+ATO+ROA+GROWTH+LEV+SHARE',data=ST).fit()
print(st_logit.summary())
Probit线性回归模型
模型形式:
Probit回归模型形式为
p ( x ) = Φ ( x ′ β ) p(x)=\Phi\left(x^{\prime} \beta\right) p(x)=Φ(x′β)
其中, Φ \Phi Φ就是标准正态分布的累积函数
模型解释:
Probit模型的系数解释不直观,但可以确定的是,当 β j > 0 \beta_j>0 βj>0时, x j x_j xj的增加会导致响应概率 p ( x ) p(x) p(x)的增加。
st_probit=sm.formula.probit('ST~ARA+ASSET+ATO+ROA+GROWTH+LEV+SHARE',data=ST).fit()
print(st_probit.summary())
模型推断
Logistic回归与Probit回归在统计推断上是一致的。
与OLS估计的多元线性回归不同的是,这两种分类回归模型采用的是极大似然估计法对模型参数进行估计,在极大似然估计的一般理论下,我们可以证明模型估计系数 β ^ \hat{\beta} β^是 β \beta β的一致估计。
基于极大似然估计的Logistic回归与Probit回归与基于OLS的多元线性回归在参数假设检验的思想上是相似的,只不过它们的检验统计量所服从的分布会有所不同。
· 单参数显著性检验
假设设置如下:
H 0 : β j = β j 0 ↔ H 1 : β j ≠ β j 0 H_{0}: \beta_{j}=\beta_{j 0} \leftrightarrow H_{1}: \beta_{j} \neq \beta_{j 0} H0:βj=βj0↔H1:βj=βj0
则单参数检验统计量为
β ^ j − β j s d ( β ^ j ) ⇒ N ( 0 , 1 ) \frac{\hat{\beta}_{j}-\beta_{j}}{s d\left(\hat{\beta}_{j}\right)} \Rightarrow N(0,1) sd(β^j)β^j−βj⇒N(0,1)
该统计量渐进服从标准正态分布,可以看到,python中播报的也是z统计量的p值。
print('logistic回归报告')
print(st_logit.summary().tables[1])
print('----------------------------')
print('probit回归报告')
print(st_probit.summary().tables[1])
· 多参数联合显著性检验
在Logit模型与Probit模型中,我们同样可以检验部分因素的统计显著性,且检验的思想依旧是比较有约束模型与无约束模型的“差异度”。
与多元线性回归模型不一样的是,分类模型没有残差平方和RSS的概念,那么联合检验的检验统计量自然也不是原来的F统计量了。但是,在似然理论下,存在一个比残差平方和更广泛的概念——离差(Deviance)
D e v i a n c e = − 2 ⋅ l o g ( l i k e l i h o o d ( m o d e l ) ) \,\,\mathrm{Deviance} =-2\cdot log\left( likelihood(model) \right) Deviance=−2⋅log(likelihood(model))
它是-2倍的模型对数似然比,而模型的对数似然比在summary播报中正是指标Log-Likelihood。
当两个模型的离差足够大时
D r − D u r > C D_{r}-D_{u r}>C Dr−Dur>C
我们便可以拒绝原假设,认为参数是联合显著的。
与其他假设检验一样,我们需要知道该检验所采用的检验统计量及其服从的分布,计算p值后再判断是否拒绝原假设。在这个检验中,似然比检验统计量定义为
L R = 2 ( l u r − l r ) = D r − D u r ∼ H 0 χ q 2 L R=2\left(l_{u r}-l_{r}\right)=D_{r}-D_{u r} \sim^{H_{0}} \chi_{q}^{2} LR=2(lur−lr)=Dr−Dur∼H0χq2
它服从自由度为约束个数 q q q的卡方分布,因此我们需要用卡方分布累积分布函数。
我们用python实现logit模型多参数显著性检验,原假设设为
H 0 : β 1 = β 2 = ⋯ = β 7 = 0 H_{0}: \beta_{1}=\beta_{2}=\cdots=\beta_{7}=0 H0:β1=β2=⋯=β7=0
#训练有约束的模型
st_logit_r=sm.formula.logit('ST~1',data=ST).fit()
# 计算检验统计量
st_logit_ll=st_logit.llf
st_logit_r_ll=st_logit_r.llf
LR=2*(st_logit_ll-st_logit_r_ll)
# 计算p值
pvalue=stats.chi2.sf(LR,7)
print('联合检验的p值为:{}'.format(pvalue))
分类预测
1.5.1 模型预测的原理
对于一组给定的解释变量取值 x 0 x_0 x0,我们将之代入模型中计算概率值 p ( x ) p(x) p(x)
p ^ ( x 0 ) = e x 0 ′ β ^ 1 + e x 0 ′ β ^ \hat{p}\left(x_{0}\right)=\frac{e^{x_{0}^{\prime} \hat{\beta}}}{1+e^{x_{0}^{\prime} \hat{\beta}}} p^(x0)=1+ex0′β^ex0′β^
这一概率是在样本自变量 x = x 0 x=x_0 x=x0下, y 0 = 1 y_0=1 y0=1的概率
# 输出st_logit模型对ST数据集前五个样本的预测p(x)
logit_pred=st_logit.predict()
print(logit_pred[:5])
规定一个阈值 α \alpha α,当概率 p ( x ) > α p(x)>\alpha p(x)>α时,样本被划分为1类,否则划分为0类。即
y ^ 0 = { 1 , p ^ ( x 0 ) > α 0 , Otherwise \hat{y}_{0}= \begin{cases}1, & \hat{p}\left(x_{0}\right)>\alpha \\ 0, & \text { Otherwise }\end{cases} y^0={1,0,p^(x0)>α Otherwise
一般情况下,阈值 α \alpha α默认为0.5。
logit_res=list()
for i in np.arange(len(logit_pred)):
if logit_pred[i]>0.5:
logit_res.append(1)
else :
logit_res.append(0)
#输出前5个样本的预测
print('前五个样本的预测结果为:{}'.format(logit_res[:5]))
1.5.2 预测结果呈现——混淆矩阵与多指标
评判模型的预测性能
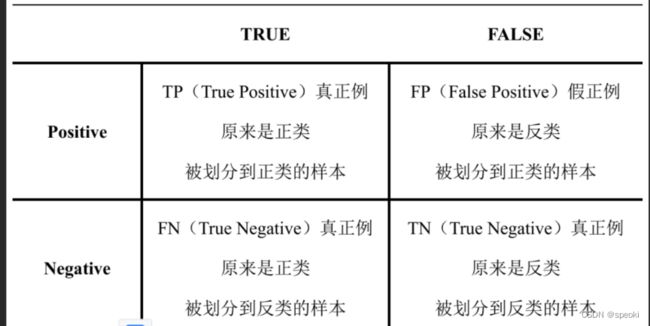
混淆矩阵
import mglearn
mglearn.plots.plot_binary_confusion_matrix()
negative通常指代“反类”,分类标签通常设置为0;
positive通常指代“正类”,分类标签通常设置为1
from sklearn.metrics import confusion_matrix
confusion_matrix(ST.ST,logit_res)
# 注意:第一个值输入的是真实的标签集,
#第二个值输入的是预测的标签集
在阈值 α = 0.5 \alpha=0.5 α=0.5下
logit模型的分类精度(也就是分类正确率),分类精度的公式为
A c c u r a c y = T P + T N T P + T N + F P + F N Accuracy=\frac{TP+TN}{TP+TN+FP+FN} Accuracy=TP+TN+FP+FNTP+TN
# 计算logits模型分类精度
logit_accuracy=(647+1)/(647+1+35+1)
print('分类精度为{}'.format(logit_accuracy))
“样本不均衡”
仅靠分类精度是远远不够。还需要引入精确率、召回率、F分数。
精确率(Precision) 衡量的是所有被预测为正类的样本中,预测正确的比例,公式为:
P r e c i s i o n = T P T P + F P Precision=\frac{TP}{TP+FP} Precision=TP+FPTP
# 以st=1为正类,计算logits模型精确率
logit_precision=(1)/(1+1)
print('精确率为{}'.format(logit_precision))
召回率(Recall) 衡量的是所有正类样本中,预测正确的比例,公式为:
R e c a l l = T P T P + F N \mathrm{Re}call=\frac{TP}{TP+FN} Recall=TP+FNTP
# 以st=1为正类,计算logits模型召回率
logit_recall=(1)/(1+35)
print('召回率为{}'.format(logit_recall))
F分数(F-score) 是精确率与召回率的调和平均,是两者的综合取舍,公式为:
F − s c o r e = 2 ⋅ p r e c i s i o n ⋅ r e c a l l p r e c i s i o n + r e c a l l F-score=2\cdot \frac{precision\cdot recall}{precision+recall} F−score=2⋅precision+recallprecision⋅recall
# 以st=1为正类,计算logits模型F分数
logit_f1=2*logit_recall*logit_precision/(logit_recall+logit_precision)
print('F分数为{}'.format(logit_f1))
还可以使用一个输出以上所有指标的函数。
from sklearn.metrics import classification_report
print(classification_report(ST.ST,logit_res))
# 注意:第一个值输入的是真实的标签集,
#第二个值输入的是预测的标签集
1.5.3 对抗不平衡数据集——改变阈值
不平衡的数据集会导致模型的训练产生偏好性,由于ST=0的样本远远多于ST=1的样本,模型会更多地学习到ST=0的样本特征,而对ST=1的样本特征学习不足,于是对于一个未知样本,模型会更倾向于将它预测成大样本的类别。
可以降低“门槛” α \alpha α,让其等于一个很小的数,这样子又可以有更多的样本被预测到ST=1的行列当中了。
logit_res=list()
for i in np.arange(len(logit_pred)):
if logit_pred[i]>0.0526:
logit_res.append(1)
else:
logit_res.append(0)
# 混淆矩阵
print(confusion_matrix(ST.ST,logit_res))
# 综合报告
print(classification_report(ST.ST,logit_res))
能改变样本预测的分布,使分布更符合我们实际的需求
需要改进预测效果,要么换一种精度更高的模型,要么进行调参处理
2. 无序多分类问题
多分类logistic的回归预测
无序多分类Logistic回归
sklearn也具有做Logistic回归的功能,但它注重预测结果输出,而在统计推断结果的可视化上,sklearn做的远远不如statsmodels。
2.1 多分类Logistic回归的两种算法
K类别的多分类Logistic回归主要有两种:
一种是修改概率映射函数,将其中一个类作为基类,通过修改过后的映射函数获得k-1个对数胜率;
另一种是“一对其余”(one-vs-rest),对每个类别都建立一个二分类Logistic回归,将本类别的样本定义为0,其余类别的样本定义为1,在所有类别的分类器中,概率 p p p最高的类别就是实际判定的类别。
2.1.1 算法1:修改概率映射函数
二分类Logistic回归的模型
log ( p ( x ) 1 − p ( x ) ) = β 0 + β 1 x 1 + ⋯ + β k x k \log \left(\frac{p(x)}{1-p(x)}\right)=\beta_{0}+\beta_{1} x_{1}+\cdots+\beta_{k} x_{k} log(1−p(x)p(x))=β0+β1x1+⋯+βkxk
等式稍微变化一下
log ( p ( y = 1 ∣ x ) p ( y = 0 ∣ x ) ) = β 0 + β 1 x 1 + ⋯ + β k x k \log \left( \frac{p(y=1|x)}{p(y=0|x)} \right) =\beta _0+\beta _1x_1+\cdots +\beta _kx_k log(p(y=0∣x)p(y=1∣x))=β0+β1x1+⋯+βkxk
多分类问题选取一个类别作为基类,分别计算0类与剩余类别之间的对数概率之比
g m ( x ) = log ( p ( y = m ∣ x ) p ( y = 0 ∣ x ) ) = β m 0 + β m 1 x 1 + ⋯ + β m k x k , m = 1 , … , M g_m\left( x \right) =\log \left( \frac{p(y=m|x)}{p(y=0|x)} \right) =\beta _{m0}+\beta _{m1}x_1+\cdots +\beta _{mk}x_k\text{,}m=1,…,M gm(x)=log(p(y=0∣x)p(y=m∣x))=βm0+βm1x1+⋯+βmkxk,m=1,…,M
这些函数的实际意义是“目标类别 j j j与基类 0 0 0的对数胜率”
使用一个变式的Logit映射函数计算每个类别的条件概率 P ( y = m ∣ x ) P(y=m\mid \mathbf{x}) P(y=m∣x)
P ( y = m ∣ x ) = e g m ( x ) 1 + ∑ m = 1 M − 1 e g m ( x ) P(y=m\mid \mathbf{x})=\frac{e^{g_m(\mathbf{x})}}{1+\sum_{m=1}^{M-1}{e^{g_m(\mathbf{x})}}} P(y=m∣x)=1+∑m=1M−1egm(x)egm(x)
在进行模型预测的时候,我们可以先选出这M-1个概率中的最大概率者,在用这个概率与阈值 α \alpha α进行比较。
2.1.2 算法2:一对其余算法
将二分类算法推广至多分类算法的一种常见方法就是“一对其余”
对每个类别都学习一个二分类模型,将这个类别与所有其余类别尽量分开,这样会生成与类别个数M相同个数的分类器,每个分类器都会输出一个概率,概率最高者“胜出”,并将这个类别的标签返回作为预测结果。
sklearn中的LogisticRegression的多分类形式就是采用了这样的算法。我们用一个含有三个类别、两个特征的玩具数据集来实操一波,来看看模型是如何处理多分类问题的
# 加载基础包
import mglearn
import matplotlib.pyplot as plt
from IPython.display import display
# 加载数据集
from sklearn.datasets import make_blobs
X,y=make_blobs(random_state=42)
print('前5个样本的X特征',X[:5])
print('前5个样本的y标签',y[:5])
# 利用散点图对数据集进行可视化
mglearn.discrete_scatter(X[:,0],X[:,1],y)
plt.xlabel('feature 0')
plt.ylabel('feature 1')
plt.legend(['class 0','class 1','class 2'])
训练一个多分类Logistic回归模型,对上述样本进行分类。
from sklearn.linear_model import LogisticRegression
logis_multi=LogisticRegression(multi_class='multinomial').fit(X,y)
# 不同于statsmodels,在sklearn中我们需要在接口fit()中填入训练模型的数据,X为自变量数据,y为因变量数据
# 查看三个分类模型的模型参数
## 截距
print(logis_multi.intercept_)
## 系数
print(logis_multi.coef_)
######将三个分类器所代表的直线画到上图中
mglearn.discrete_scatter(X[:,0],X[:,1],y)
line_x=np.linspace(-15,15)
for coef,intercept,color in zip(logis_multi.coef_,logis_multi.intercept_,['b','r','g']):
plt.plot(line_x,-(line_x*coef[0]+intercept)/coef[1],c=color)
plt.ylim(-10,15)
plt.xlim(-10,8)
plt.xlabel('feature 0')
plt.ylabel('feature 1')
plt.legend(['class 0','class 1','class 2','line class 0','line class 1','line class 2'],loc=(1.01,0.3))
3. 以预测为目的分类问题实操流程——基于sklearn
3.1 划分训练集/测试集
#加载函数
from sklearn.model_selection import train_test_split
#数据集切分
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.25,random_state=0)
# test_size为测试集数据量占原始数据的比例
print('train_size',len(X_train)/len(X))
print('test_size',len(X_test)/len(X))
3.2 训练模型/模型预测
from sklearn.linear_model import LogisticRegression
# 使用训练集进行训练
logit_multi=LogisticRegression(multi_class='multinomial').fit(X_train,y_train)
# 使用测试集进行预测
y_pred=logis_multi.predict(X_test)
# 查看预测结果
print(y_pred)
3.3 预测结果分析
完成预测后,我们需要对模型的预测结果进行分析,常见的分析指标有:分类精度,精确率,召回率,f分数等;当然,我们可以输出混淆矩阵。