【论文笔记】—目标姿态估计—EPro-PnP—2022-CVPR

题目：EPro-PnP: Generalized End-to-End Probabilistic Perspective-n-Points for Monocular Object Pose Estimation

该论文被评为2022最佳学生论文，作者是同济大学的陈涵晟。

DOI：10.48550/arXiv.2203.13254

时间：2022-3-24上传于arxiv
会议：2022-CVPR
机构：同济大学 & 阿里巴巴

论文链接：【论文链接】
代码链接：【代码链接】
论文十问：【论文十问】

提出问题：

对于单目物体位姿估计任务，基于PnP的几何优化方法需要通过深度网络提取图像中的2D-3D关联点，然后求解PnP问题得到物体的位姿。但因为PnP本质上不可导，难以通过反向传播PnP输出的位姿来训练网络。

解决方案：

在不知道物体形状的情况下，仅用端到端位姿损失就能训练网络去预测所有的2D/3D点及其关联权重。

本文将位姿优化问题转变为预测位姿概率密度的问题，提出了端到端概率PnP（EPro-PnP），从而实现了通过监督位姿的概率分布来端到端地训练网络，使网络可以自主学习2D-3D关联点而不必强加代理损失。

创新点：

将PnP位姿优化问题转变为预测位姿概率密度的问题。对于一个基于PnP的物体位姿估计网络，可以通过反向传播位姿的概率密度从而学习物体的2D-3D关联，实现稳定的端到端训练。

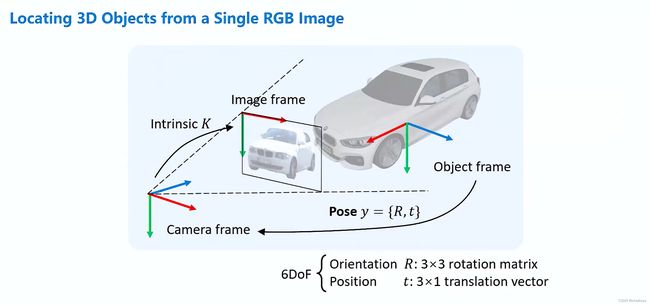
动机：从单张的RGB图片中去定位一个3D的物体。

给定物体的投影Image frame，求解物体的坐标系Object frame到相机坐标系Camera frame的刚体变换。
(刚体变换：物体到相机的一个相对位姿。包含两部分：1、朝向；2、位置。)

基于几何的位姿估计PnP方法：

在图像坐标系和3D物体坐标系分别找到n个相关联的2D和3D点，对应的这个2D的图像坐标和3D的物体坐标，从这些点中可以构建一个集合投影的约束，物体的位姿被隐式地去定为了优化问题的─个最优解（优化物体的位姿y：使得每一个3D点通过位姿变换投影到图像上后它与2D点之间的重投影的误差最小化，这样得到的最优位姿即PnP的位姿解）

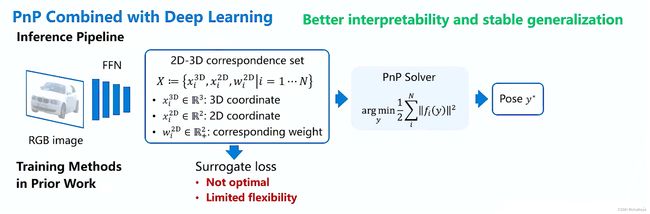
问题的本质：想办法找到这些2D点和3D点。

一般方法：通过一个前馈网络输入一张RGB图像，去预测2D点和3D点。同时还可以预测每一个关联点的权重，构成一个加权问题。以往的方法需要直接监督这些2D点和3D点，构建一个所谓的surrogate loss(代理损失)，但对于位姿来说它并非是最优的一个训练的目标。

以往方法举例：

1. 基于关键点Keypoints的方法：已知物体的形状可以首先定义一些3D点，网络的任务就是找到这些2D点的位置。
2. Dense correspondence：把2D点固定在图像上的一个像素的中心位置，每个像素需要去预测对应的一个3D的坐标X、Y、Z。然后还要粑图像的前景也就是mask给导出来。

上两种方法都是相应的把问题进行了一个转化，直接去监督这些东西的变量，但是会有诸多的限制，比如说我们必须得知道它的形状。

而本论文不需要知道知道它的形状，只知道数据集中只标了物体的位姿的情况下，是否可以通过反向传播包括这个PnP这么一层来去学习这些中间变量。

关键：把PnP求解器变成一个可微分的一个Layer(层)，或者说是一个模块，使得它在整个网络中可以实现一个端到端的训练。

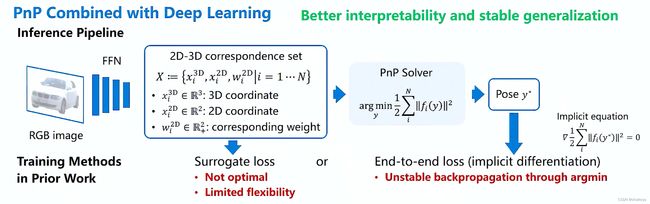
以前的方法：lmmplicit differentiation（隐式微分），但是有一个问题arg min函数并不是真正完全可导的，在某些点是不连续的，所以会导致反向传播不稳定，就必须要依赖整个代理损失来做一个正则化，来保证整个PnP它优化的目标函数如果它是一个凸优化问题的话，然后用隐式微分就可以解决，但是如果没有前面这些东西，光靠端到端的一个损失函数，没有办法稳定的通过反向传播来学习所有的这些2D、3D点。 

本文试图把不可微分的—个最优解deterministic pose固定的一个单独位姿把它变成一个可微的东西。用了概率框架，把PnP视角转换一下，输出一个关于位姿的概率分布。输入Correspondence X是一个可导的东西，通过经典的贝叶斯公式推导得到一个概率密度。

1. Define the likelihood function：定义一个似然函数，通过重授影误差的─个平方和，来取负号再取exp，可以得到关于位姿的一个likelihood似然。
2. Prior：先验使用一个无信息的uninformative prior，其实是一个flat prior(扁平先验)的求码小模，可以直接粑整个likelihood做一个normalization归—化，就得到了最终的后验的─个概率密度，即图右上角的分布。

实质上是分类的Softmax在一个连续域上的推广，因为实际Softmax它就是用类似的一种方法Sumation（求和）在离散的类别上的求和，但本文是一个积分的情况，一个不可导的arg min问题来变成一个可导的问题。

这是因为优化层中的argmin函数不可导，因此最优位姿不可导，但将位姿视为概率分布后，位姿的概率密度是可导的。从本质上来说，这一做法等同于训练分类网络时，将argmax层替换为softargmax（即softmax）层，本文实际上是将离散softmax推广到了连续分布上。

损失函数：

得到一个具体的分布后，损失函数的反向传播是基于KL Divergence来计算和真值之间的误差，和分类里面的cross entropy交叉嫡它本身是一回事，是一个连续的cross entropy。

实现具体分布的KL Divergence计算时用蒙特卡洛的方法对这个分布做一个近似，

启发1：【DSAC】做一个可微分的RANSAC，解决思路是RANSAC本身需要很多的—个hypothesis(假设)，我们要从中去选择一个比较好的hypothesis(假设)，取arg max，但为了使其变成一个可学习的过程使用了softmax，来把hypothesis对应的一个score变成一个可学习的东西，有限的hypothesis的pool中去选择最优的一个解，其实也不是一个连续意义上的东西。

启发2：【Deep SDF】预测一个物体的3D物体的表面得到他的一个几何结构。也是一个隐式的方法，需要去找到表面的一个位置，但是很难直接去预测表面的各个点，所以把它变成预测一个signed distance function（符号距离函数），输入x是3D空间的三维坐标，输出的s是各个点到物体表面的距离（外面SDF>0，里面的SDF<0），通过采样的方法来训练得到一个SDF。

网络结构：

【方案一】是6DoF Pose Estimation 的Benchmark上现有的网络CDPN，—个Surrograte loss(代理损失)来直接监督confidence map(置信图)和3D坐标，把它原始的这个PnP换成EPro-PnP，去做一个端到端的反向传播的训练。

【方案二】更加激进一点的方案：验证EPro-PnP是可以不需要3D坐标的回归损失，只用端到端的损失，把3D坐标2D坐标还有关联权重一起学出来。

参考Deformable DETR，首先用defformable samplling的一个模块去预测2D点，确定没一个物体的中心参照点，然后去预测各个2D点对于参照点的偏移，就可以得到这些2D点的位置。然后从一个特征中通过interpolation（插值）来得到各个点的特征，经过一些处理，用很小的Transformer做一些信息交互，然后就得到各个点对应的3D坐标和权重。整个框架是做3D物体检测的，还需要各个点的特征聚集起来得到一个物体的特征，来预测整个物体的一些属性。

实验结果：

图6-EPRO-PNP的灵活性允许预测具有强大表达能力的多模态分布，成功捕获方向模糊性，而无需离散多箱分类或复杂的混合模型。

图7-LineMOD 测试数据上推断的权重和坐标图的可视化。

当使用预训练的CDPN初始化时，EPro-PNP继承了详细的几何轮廓，因此将活动权重限制在前景区域内并实现整体最佳性能。