使用循环神经网络预测温度
简介
本文以天气时间序列数据集为例,讨论如何使用深度学习模型预测未来天气温度。
使用的是由德国耶拿马克思普朗克生物地球化学研究所的气象站记录。
数据每10分钟记录一次,共记录14种不同的量,如气温、气压、湿度、风向等,原始数据可追溯到2003年,本例只使用2009-2016年的数据。
数据
下载并解压数据略。
加载数据:
data_dir = r'E:\practice\tf2\temperature'
fname = os.path.join(data_dir, 'jena_climate_2009_2016.csv')
f = open(fname)
data = f.read()
f.close()
lines = data.split('\n')
header = lines[0].split(',')
lines = lines[1:]
print(header)
print(len(lines))
如下图:
查看温度:
# 解析数据到Numpy向量
import numpy as np
float_data = np.zeros((len(lines), len(header) - 1))
for i, line in enumerate(lines):
values = [float(x) for x in line.split(',')[1:]]
float_data[i, :] = values
# 查看温度序列
from matplotlib import pyplot as plt
temp = float_data[:, 1]
plt.plot(range(len(temp)), temp)
plt.title('All days temperature')
plt.legend()
plt.figure()
# 全部的数据不容易看清楚,查看前10天的数据
plt.plot(range(1440), temp[:1440])
plt.title('First 10 days temperature')
plt.legend()
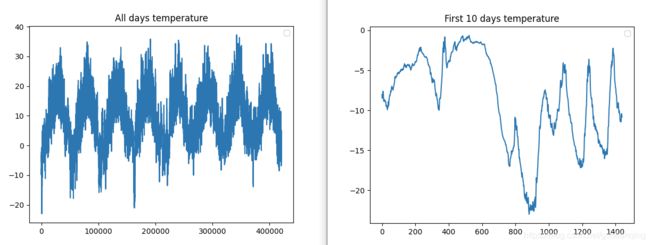
plt.show()
如下图:
准备数据
用数学语言重新描述一下问题:
一个时间步是10分钟,每个steps有一个数据点,给定过去lookback个时间步之内的数据,预测delay个时间步之后的温度。
假定:
- lookback = 720,即给定过去5天内的数据
- steps = 6,即采样频率1小时
- delay = 144,即预测未来24小时后的温度
开始数据预处理:
# 数据标准化
mean = float_data[:200000].mean(axis = 0)
float_data -= mean
std = float_data[:200000].std(axis = 0)
float_data /= std
由于数据集中样本高度冗余,编写一个数据生成器,使用原始数据即时生成样本:
# 生成器:生成时间序列样本及其目标
def generator(data, lookback, delay, min_index, max_index, shuffle = False, batch_size = 128, step = 6):
if max_index is None:
max_index = len(data) - delay - 1
i = min_index + lookback
while 1:
if shuffle:
rows = np.random.randint(min_index + lookback, max_index, size = batch_size)
else:
if i + batch_size >= max_index:
i = min_index + lookback
rows = np.arange(i, min(i + batch_size, max_index))
i += len(rows)
samples = np.zeros((len(rows), lookback // step, data.shape[-1]))
targets = np.zeros((len(rows), ))
for j, row in enumerate(rows):
indices = range(rows[j] - lookback, rows[j], step)
samples[j] = data[indices]
targets[j] = data[rows[j] + delay][1]
yield samples, targets
各参数说明如下:
- data: 浮点数组成的原始数组
- lookback: 输入数据应该包括过去多少个时间步
- delay: 目标应该在未来多少个时间步之后
- min_index和max_index:data数组中的索引,用于界定需要抽取哪些时间步。这有助于保存一部分数据用于验证,另一部分用于测试
- shuffle: 是否打乱样本
- batch_size;批量样本数量
- step:数据采样周期,设置为6,表示每小时取样一次
输出为(samples, targets)无组,其中,samples是输入数据中的一个批量,targets是对应的目标温度数组。
使用上述函数准备训练生成器、验证生成器和测试生成器:
lookback = 1440
step = 6
delay = 144
batch_size = 128
train_gen = generator(float_data, lookback = lookback, delay = delay, min_index = 0, max_index = 200000, shuffle = True, step = step, batch_size = batch_size)
val_gen = generator(float_data, lookback = lookback, delay = delay, min_index = 200001, max_index = 300000, step = step, batch_size = batch_size)
train_gen = generator(float_data, lookback = lookback, delay = delay, min_index = 300001, max_index = None, step = step, batch_size = batch_size)
val_steps = (300000 - 200001 - lookback) // batch_size
test_steps = (len(float_data) - 300001 - lookback) // batch_size
建立最低基准
在进行机器学习预测温度之前,我们最好有一个最低的标准,这样才能更好地评估模型预测的结果是否靠谱。
最低基准,应该就是通过常识得到的预测。对于温度,我们有理由预测未来24小时的温度与当前温度相同。
评估一下:
# 对比基准,基于常识的预测结果
def evaluate_native_method():
batch_maes = []
for step in range(val_steps):
samples, targets = next(val_gen)
preds = samples[:, -1, 1]
mae = np.mean(np.abs(preds - targets))
batch_maes.append(mae)
print(np.mean(batch_maes))
evaluate_native_method()
celsius_mae = 0.29 * std[1]
print(celsius_mae)
得到MAE为0.29。把它转化为温度的平均绝对误差,为2.57度。
下面看看深度学习模型能不能把这个误差减小。
密集连接模型
在开始一项深度学习研究时,常常会使用简单的模型对问题先进行处理,再进行较为复杂的模型研究。
而密集连接模型较为简单,且计算代价不高,可以直接搞起:
# 首先使用简单的密集连接网络进行预测
from keras.models import Sequential
from keras import layers
from keras.optimizers import RMSprop
model = Sequential()
model.add(layers.Flatten(input_shape = (lookback // step, float_data.shape[-1])))
model.add(layers.Dense(32, activation = 'relu'))
model.add(layers.Dense(1))
model.compile(optimizer = RMSprop(), loss = 'mae')
history = model.fit_generator(train_gen, steps_per_epoch = 500, epochs = 20, validation_data = val_gen, validation_steps = val_steps)
# 绘图
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label = 'Training loss')
plt.plot(epochs, val_loss, 'b', label = 'Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
结果如下:
可见,这个预测结果并不可靠,战胜常识得到的最低基准并不容易。
常识是一个很简单的模型,使用深度学习的复杂框架却学习不到这个模型,这也是深度学习存在的一个问题。
使用循环网络
基于温度数据的预测,是有序的数据。拿3个月前的数据来预测明天的温度,差别就会很大。
而密集连接网络把时间序列展开,就删除了时间序列的概念。
使用循环网络的GRU层可以以较低的计算低价把时间序列引入到预测中去:
# 基于GRU的模型
from keras.models import Sequential
from keras import layers
from keras.optimizers import RMSprop
model = Sequential()
model.add(layers.GRU(32, input_shape = (None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer = RMSprop(), loss = 'mae')
history = model.fit_generator(train_gen, steps_per_epoch = 500, epochs = 20, validation_data = val_gen, validation_steps = val_steps)
# 绘图
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label = 'Training loss')
plt.plot(epochs, val_loss, 'b', label = 'Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
结果有所提高,但过拟合却较严重,还有提升空间。
使用循环dropout降低过拟合
dropout,就是将某一层的输入单元随机设置为0,目的是打破该层训练数据中的偶然相关性。
keras每个循环层都有两个与dropout相关的参数:
- dropout: 浮点数,指定该层输入单元的dropout比率
- recurrent_dropout: 指定循环单元的dropout比率
注意,添加dropout后,网络需要更长的时间才能完全收敛,所以网络训练轮次增加为原先的2倍。
如下:
# 使用循环dropout降低过拟合
model = Sequential()
model.add(layers.GRU(32, dropout = 0.2, recurrent_dropout = 0.2, input_shape = (None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer = RMSprop(), loss = 'mae')
history = model.fit_generator(train_gen, steps_per_epoch = 500, epochs = 40, validation_data = val_gen, validation_steps = val_steps)
# 绘图
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label = 'Training loss')
plt.plot(epochs, val_loss, 'b', label = 'Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
过拟合大大降低了,预测结果也更加稳定,但效果并没有好很多。
循环层堆叠
模型不再过拟合,但似乎遇到了性能瓶颈,可以考虑增加网络容量。
增加网络容量的通常做法是增加每层单元数或增加层数。循环层堆叠是构建更加强大网络的经典方法。
如下:
# 堆叠GRU模型
model = Sequential()
model.add(layers.GRU(32, dropout = 0.1, recurrent_dropout = 0.5, return_sequences = True, input_shape = (None, float_data.shape[-1])))
model.add(layers.GRU(64, activation = 'relu', dropout = 0.1, recurrent_dropout = 0.5))
model.add(layers.Dense(1))
model.compile(optimizer = RMSprop(), loss = 'mae')
history = model.fit_generator(train_gen, steps_per_epoch = 500, epochs = 40, validation_data = val_gen, validation_steps = val_steps)
# 绘图
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label = 'Training loss')
plt.plot(epochs, val_loss, 'b', label = 'Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
结果有所改进,但并不显著。过拟合并不严重,还可以增加网络容量。但添加网络容量对于效果的影响并不会线性增加。
使用双向RNN
RNN是按顺序处理输入序列的时间步,而打乱或反转时间步会完全改变RNN从序列中提取的表示。
双向RNN利用了RNN的顺序敏感性,它包含两个普通的RNN,每个RNN分别沿着一个方向对输入序列进行处理,然后将它们的表示合并在一起。
通过这样处理,双向RNN能够捕捉到可能被单向RNN忽略的模式。
代码如下:
# 使用双向RNN
model = Sequential()
model.add(layers.Bidirectional(layers.GRU(32), input_shape = (None, float_data.shape[-1])))
model.add(layers.Dense(1))
model.compile(optimizer = RMSprop(), loss = 'mae')
history = model.fit_generator(train_gen, steps_per_epoch = 500, epochs = 40, validation_data = val_gen, validation_steps = val_steps)
# 绘图
import matplotlib.pyplot as plt
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(1, len(loss) + 1)
plt.figure()
plt.plot(epochs, loss, 'bo', label = 'Training loss')
plt.plot(epochs, val_loss, 'b', label = 'Validation loss')
plt.title('Training and Validation loss')
plt.legend()
plt.show()
这个模型的表现与普通GRU层差不多,因为所有有效的预测都来自正常顺序的好一半网络。
毕竟,对于温度预测的问题,反向顺序并不会得到有用的表示。
对于影评,可能会有较好的表现。因为单词都在那里,反向可能会抓取的信息更多一点。
小结
本文展示了处理温度预测问题的整个过程。
对问题分析、数据处理、基准建立、模型应用、模型改进、过拟合等过程进行了描述。
对于本例,还有很多可以优化的工作可以处理,如增大循环层中单元个数、调用优化器学习率等。
参考资料
《Python深度学习》