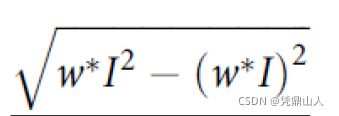图像均值、标准差、变异系数的意义

目录

均值图像如何算？

方差图像如何计算？

变异系数是什么？

极差：最大值-最小值

方差：数列中每个元素与均值之差的平方和

标准差：方差的开平方根

变异系数 = （正态分布）标准差 / 平均值

---

先来下个定义

• 均值反映了图像的亮度，均值越大说明图像亮度越大，反之越小；
• 标准差反映了图像像素值与均值的离散程度，标准差越大说明图像的质量越好（说明图像边缘清晰）
• 变异系数可以消除图像中不同区域灰度变化范围不一致的影响（比如黑色区域和白色区域相间的图片），更能反映出离散程度，变异系数越大说明边界越清晰

        图像的均值和均值图像是不同的，图像均值是指整幅图的平均值，是一个具体的数值，均值图像是指对图像做均值滤波之后的图像

        同样，图像的标准差和标准差图像也是不同的，图像标准差是整幅图像的标准差，是一个具体的数值，标准差图像是指对图像每一个像素值进行标准差计算，得到的图像叫做标准差图像。

图像均值和方差可以用OpenCV的公式：

void cv::meanStdDev (
    InputArray  src, 
    OutputArray     mean,
    OutputArray     stddev,
    InputArray  mask = noArray() 
)   


cvtColor(image, gray, CV_RGB2GRAY);
Mat mean,stddev;
meanStdDev(gray, mean, stddev);
double meanValue = mean.at(0, 0);
double stdDev = stddev.at(0, 0);

均值图像如何算？

均值图像可用均值滤波来计算

w * I : 其中w 是均值滤波核（当然也可以是高斯核）， I 是灰度图

方差图像如何计算？

由于图像可以看做是离散型二维随机变量，离散型二维随机变量的计算公式如下：

所以，方差可以由如下公式计算：

下面引入局部对比度的概念，局部对比度是由方差图像除以均值图像（每个像素都参与计算）

变异系数是什么？

方差除以均值的物理意义是变异系数，在解释变异系数之前，先来把其它概念介绍清楚：

对于一个数字序列：1,3,5,7,9,100,200,200,305

• 极差：最大值-最小值

                物理意义：粗略地说明数据的变动范围

                优点: 简单易理解，计算简单明了

                缺点：受数据极端值影响，反应数列离散程度也较粗糙，不能反应数列内容的发散

                            情况，即使样本不大，极差带来的发散误差也较大

        为了应对极差的明显缺点，如果要很仔细很全面地考察数列的发散程度，就必须考虑数列中每个元素的彼此发散情况。这时，需要引进方差的概念。

• 方差：数列中每个元素与均值之差的平方和

                为什么要用平方和，下面讲的很清楚：

 为了消除方差因为平方而带来的，与原数列的量纲不一致的情形，进一步有了标准差的概念，

• 标准差：方差的开平方根

                        优点：标准差可以用来完美地表示数据的离散程度,标准差与均值相结合，可以

                                    描述正态分布特征，即估计正态分布下数据的频数分布情况。

如果要更进一步，如何来对比二个完全不同项目（单位不一样，比如一个是身高、一个是智力）的数列的离散程度，或者虽然都是比较重量但一个数字序列是书籍的重量另一个数字序列是每粒瓜子的重量（单位相同但平均值不同）的二个序列的离散程度，如何比较呢，这个时候，需要更进一步引入变异系数的概念：

• 变异系数 = （正态分布）标准差 / 平均值

                        优点：变异系数既可以消除二个数字序列值平均水平不同对离散程度比较的

                                影响，还可消除二个序列因为量纲单位不同而造成的评价对比影响，从而

                                更完美地反映数列离散程度的大小。