算法提高之搜索:剪枝与与优化
目录
- 0、剪枝的方法
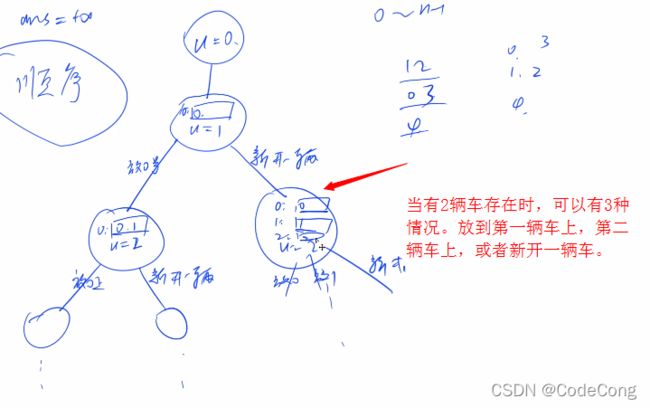
- 1、小猫爬山
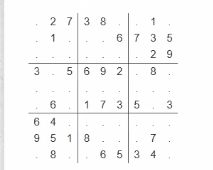
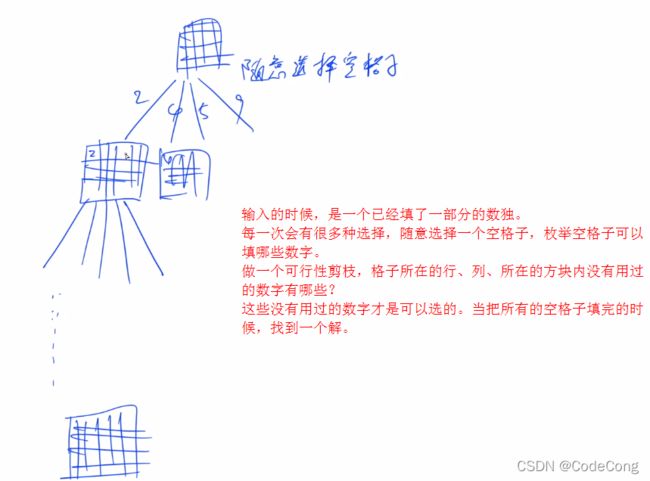
- 2、数独
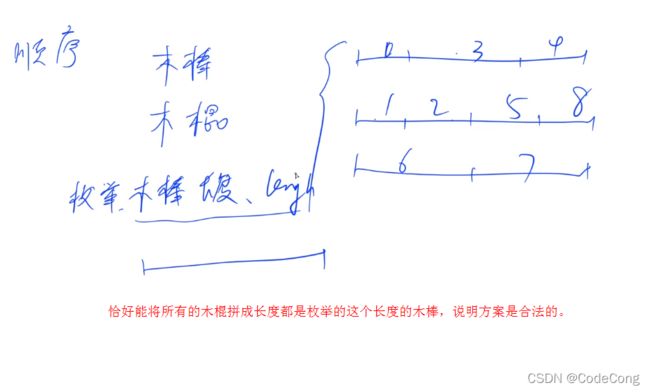
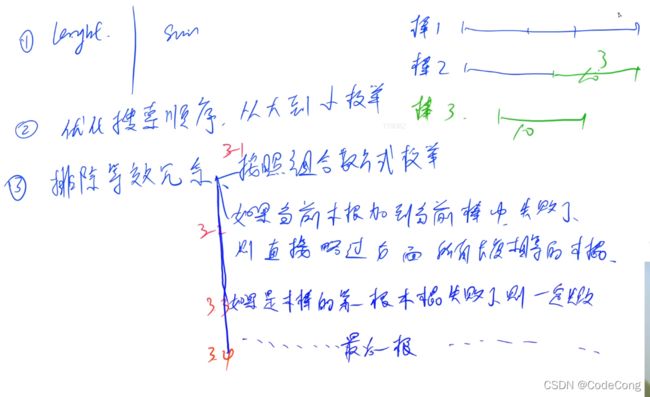
- 3、 木棒
- 4、 生日蛋糕
0、剪枝的方法
1、小猫爬山
#include 2、数独
/*
81个字符的字符串->在计算中变向转换成9*9的矩阵。
将变向的9*9矩阵转换到,每一行、列和九宫格的9位的01串(int) draw实现
9位的01串从右向左依次表示123456789是否存在。0表示存在,1表示不存在可填。
预处理 0~1<<8 01串中1的个数。
log2(0) log2(1) log2(8) 中的n 目的是当某个01串,首位是1,其他位是0.得到1的位置。
init->将行、列、九宫格的01串全部置成1。
draw:最初将变向的9*9矩阵转换到,每一行、列和九宫格的9位的01串。
在dfs中设置01串中1的位置为0,以及将0的位置变成1。
lowbit:返回一个01串中,最后一个1,以及它后边的0.
*/
/*
预处理 one map为二进制优化做准备
初始化 将所有行、列、九宫格的01串全部变成1.
draw 将字符串中还有数字的地方修改到01串中。计算空格数。
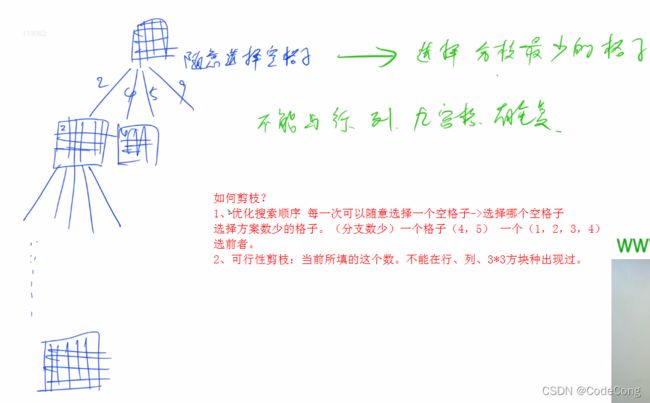
dfs以空格为0试截止。先找到所有空格中分支最少的空格。
对分支最少的空格优先dfs。
*/
#include 3、 木棒
#include 4、 生日蛋糕




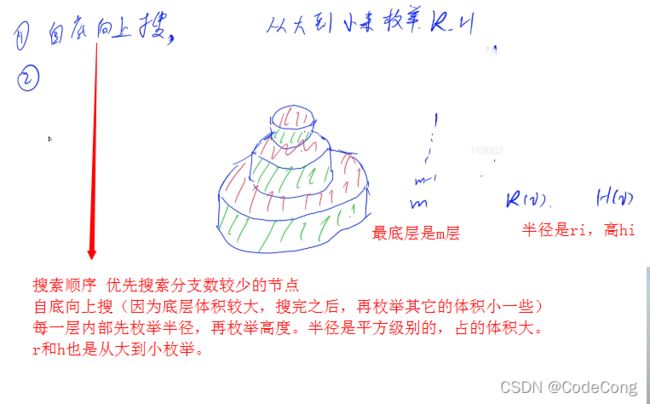
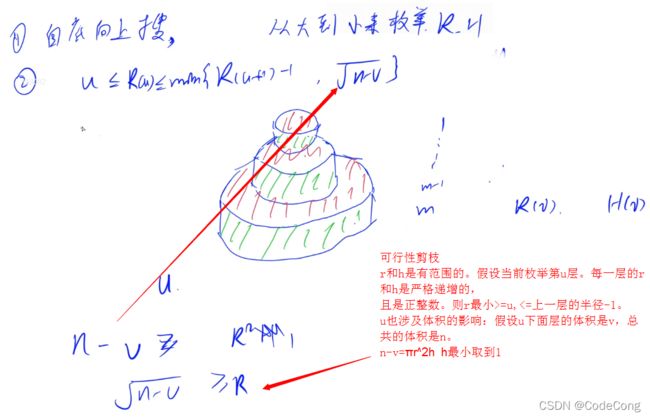

从第一层到第u层的最小体积和最小面积



ans是当前最小的表面积

#include