CNN实验报告
不同模块对CNN的影响
- 介绍
-
- 实验环境
- 网络结构
- 默认情况
- (一)添加BN
- (二)激活函数
-
- 1. tanh
- 2. LeakyReLU
- 3. sigmoid
- (三)正则化
-
- L2正则
- DropOut
- (四)优化器
-
- Adam
- (五)学习率衰减
-
- learning_rate=0.01
- 学习率衰减
- (六)参数初始化
-
- kaiming_normal_
- xavier_normal_
- (七)综合测试
- 一个说明
介绍
本次实验将使用两个CNN网络模型,分别在MNIST数据集上测试,并不断微调网络结构和参数,查看这些操作对模型的影响。
实验环境
- python 3.8
- Pytorch 1.8.1,gpu版本
- IDE:Jupyter Notebook
网络结构
本次实验使用两种网络结构
- 单层卷积: 一层卷积+一层池化+两层全连接
# 单层结构:一层卷积 + 一层池化 + 两层全连接 class Net1(nn.Module): def __init__(self,): super(Net1,self).__init__() self.conv_unit = nn.Sequential( # out-> [26,26,10] nn.Conv2d(1, 10, kernel_size=3, stride=1, padding=0), nn.ReLU(), # out->[13,13,10] nn.MaxPool2d(kernel_size=2, stride=2) ) self.fc_unit = nn.Sequential( nn.Flatten(), nn.Linear(13*13*10, 120), nn.ReLU(), nn.Linear(120,10) ) def forward(self, x): x = self.conv_unit(x) x = self.fc_unit(x) return x - 多层网络:三层卷积+两层池化+两层全连接
# 多层结构:三层卷积 + 两层池化 + 两层全连接
class Net2(nn.Module):
def __init__(self):
super(Net2, self).__init__()
self.conv_unit = nn.Sequential(
# out-> [24,24,40]
nn.Conv2d(1, 40, kernel_size=5, stride=1),
nn.ReLU(),
# out->[12,12,40]
nn.MaxPool2d(kernel_size=2, stride=2),
# out->[10,10,10]
nn.Conv2d(40, 20, kernel_size=3, stride=1),
nn.ReLU(),
# out->[5,5,20]
nn.MaxPool2d(kernel_size=2,stride=2),
# out->[3,3,20]
nn.Conv2d(20,20,kernel_size=3, stride=1),
nn.ReLU()
)
self.fc_unit = nn.Sequential(
nn.Flatten(),
nn.Linear(3*3*20,100),
nn.ReLU(),
nn.Linear(100, 10)
)
def forward(self,x):
x = self.conv_unit(x)
x = self.fc_unit(x)
return x
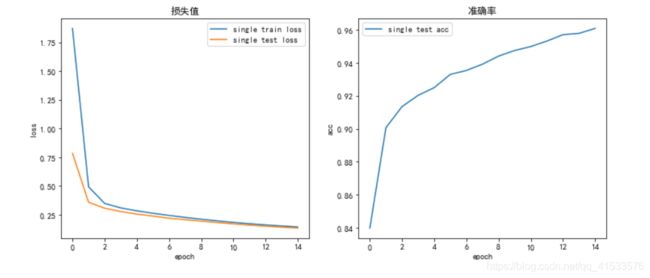
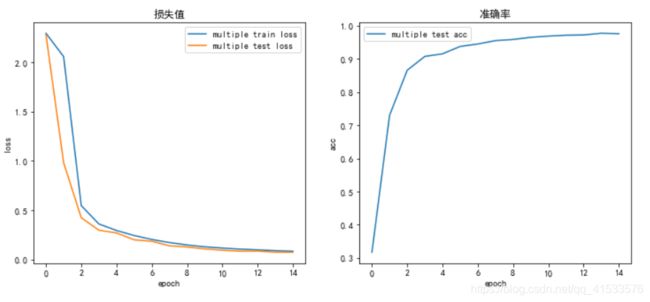
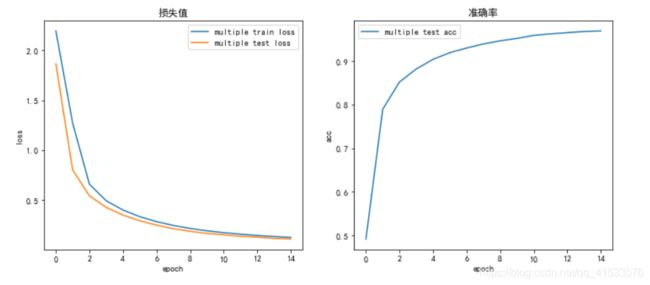
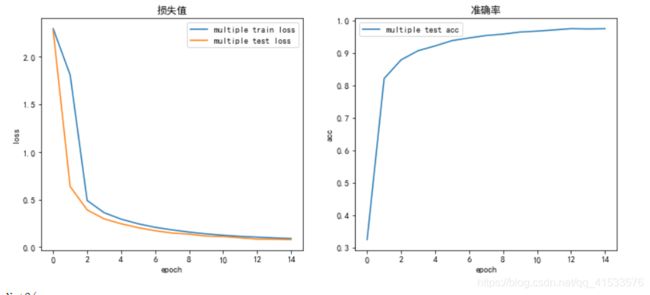
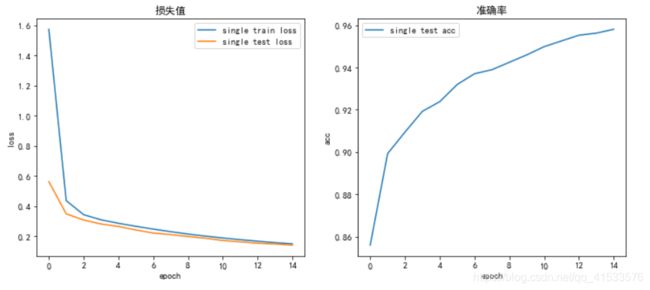
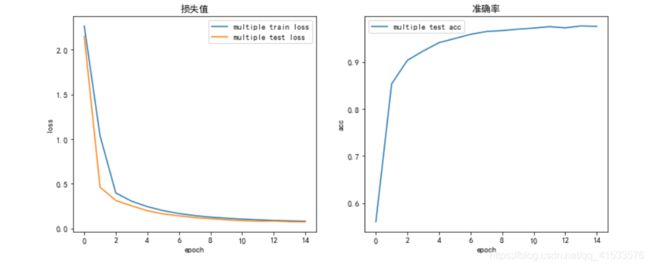
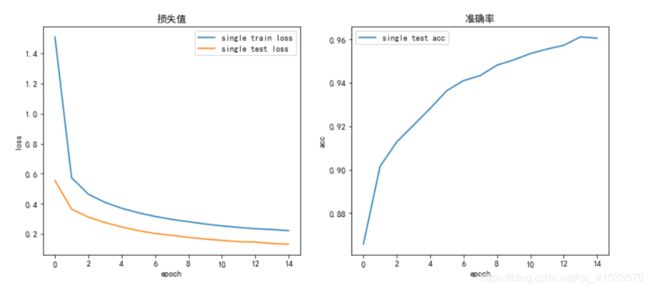
默认情况
用以下参数作为初始的默认情况训练15个epoch。可将默认情况下的训练结果当做一个基准,在其后不断对网络进行微调(每次仅对结构做一个改变),观察结果变化情况。
注:后续实验中若无说明,网络的结构和下列参数不做更改
- batch size为128
- learning rate为0.001
- 采用ReLU激活函数
- 使用交叉熵损失函数
- SGD方式优化(momentum为0.9)
结果如下表所示:
| train loss | test loss | acc | |
|---|---|---|---|
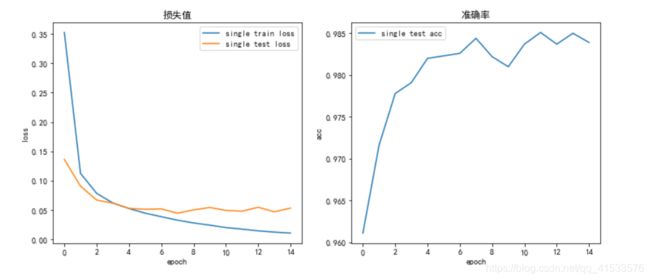
| 单层网络 | 0.1444 | 0.1347 | 96.09 % |
| 多层网络 | 0.0847 | 0.0748 | 97.57 % |
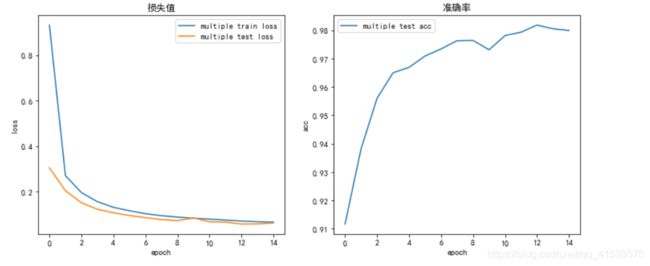
多层卷积网络效果好于单层卷积网络,前者最终准确率优于后者,这是因为网络深度加深,使模型的拟合能力加强,对特征的提取和压缩也做的更好,这是多层网络的优势。
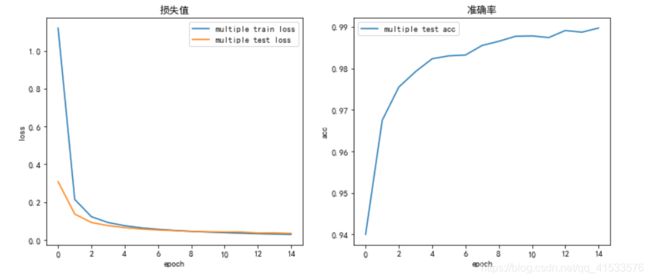
(一)添加BN
在默认情况下,在网络中添加batch normalization,查看此时的网络结构与效果
效果如下表所示:
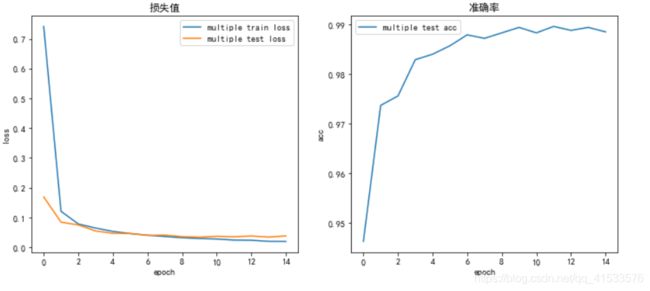
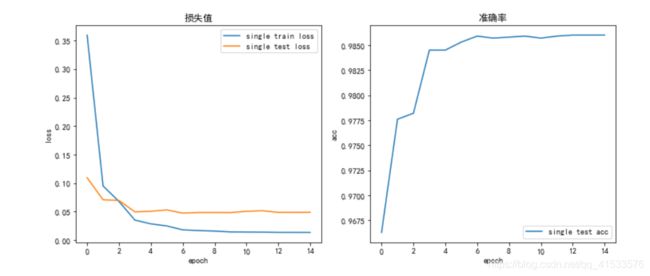
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.0524 | 0.0566 | 98.14 % |
| 多层网络 | 0.0289 | 0.0342 | 98.6 % |
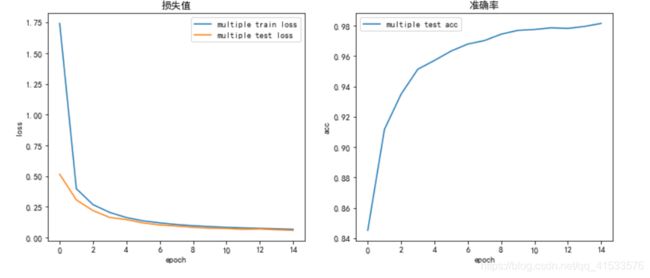
添加batch normalization后,单、多层网络与默认情况相比表现均有所提升,准确率上升1个百分点以上,且模型的收敛速度更快,说明BN对模型训练有加速效果。特别需要注意的是,在多层网络上加速收敛效果尤为明显,通过BN操作,将初始epoch的测试准确率提高至94%,与未加BN的比较好了很多。
(二)激活函数
原网络使用ReLU激活函数,下面更换不同的激活函数
1. tanh
将ReLU更改为tanh,展示效果
效果如下表所示:
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.1990 | 0.1901 | 94.59 % |
| 多层网络 | 0.1242 | 0.1076 | 96.89 % |
tanh激活函数的表现一般,两种网络的准确率均有下降,但下降幅度不大。
2. LeakyReLU
将ReLU更改为LeakyReLU
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.1536 | 0.1411 | 95.84 % |
| 多层网络 | 0.0921 | 0.0810 | 97.47 % |
模型效果并无很大的改善。
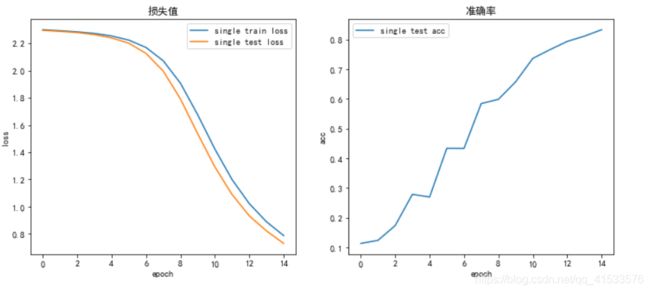
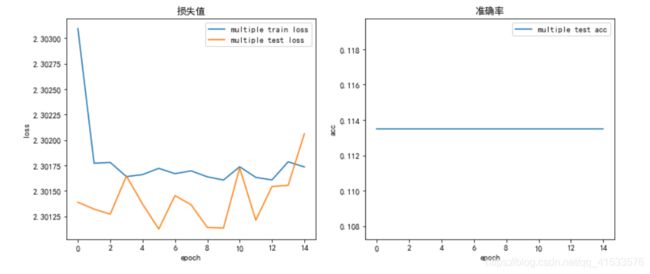
3. sigmoid
将ReLU改为sigmoid
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.7874 | 0.7295 | 83.3 % |
| 多层网络 | 2.3017 | 2.3020 | 11.35 % |
使用sigmoid激活函数时,表现非常差,单层网络准确度下降十几个百分点,而多层网络无法正常工作,test loss值不断跳跃,变化幅度缓慢,说明使用sigmoid激活函数造成了梯度饱和,无法对参数值正常迭代,导致准确率无法上升,仅为11.35%,说明在这个多层网络中,不能使用sigmoid作为激活函数。
(三)正则化
L2正则
在网络中添加L2正则化,pytorch很容易可以实现,定义优化器时加入参数weight_decay,即设定L2正则化中的 λ \lambda λ数值,这里设置为1e-4,观察效果,即
optimizer = optim.SGD(model_single.parameters(),
lr=learning_rate,momentum=0.9, weight_decay=1e-4)
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.1486 | 0.1404 | 95.72 % |
| 多层网络 | 0.0808 | 0.0738 | 97.56 % |
训练结果变化不明显,但是可以看到,初始准确率较默认情况还是有上升,有一定的加速作用。
DropOut
在网络中加入DropOut层,将丢弃概率设置为0.3
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.2200 | 0.1296 | 96.04 % |
| 多层网络 | 0.1869 | 0.0871 | 98.6 % |
单层网络添加DropOut使最终的准确率下降了,而在多层网络中准确率有所上升,可能原因为单层网络中模型拟合能力较多层网络弱,在丢弃后对数据的拟合能力进一步下降,导致准确率下降,而多层网络丢弃恰好改进了过拟合,使得最终准确率有所上升。
无论是单层还是双层,其test loss最后与train loss 的差距越来越大,考虑是学习率的问题导致在测试集上收敛过快。
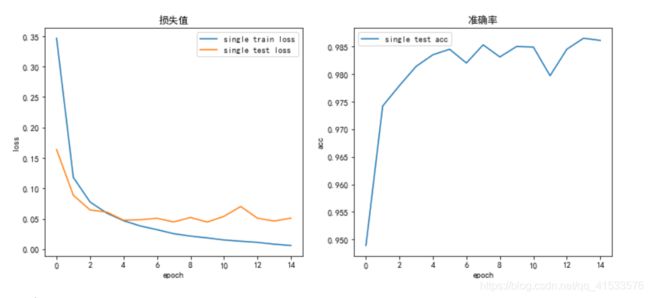
(四)优化器
Adam
将原本的SGD优化器改换为Adam优化器
附:Adam优化器的几个问题、Adam优化算法的简单介绍
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.0060 | 0.0510 | 98.61 % |
| 多层网络 | 0.0149 | 0.0311 | 98.97 % |
Adam优化器的表现优于SGD,二者的准确率均有提升,但是在训练后期都出现了过拟合问题,test loss和test acc起伏较大。
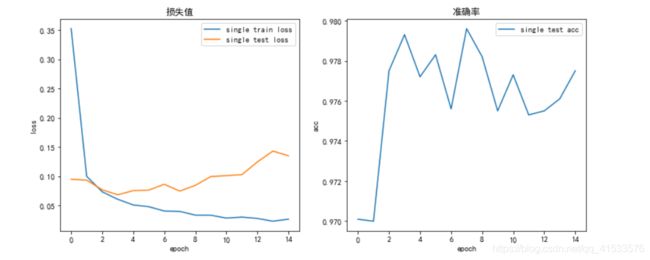
(五)学习率衰减
learning_rate=0.01
将学习率提至0.01
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.0261 | 0.1347 | 97.75 % |
| 多层网络 | 0.0196 | 0.0381 | 98.85 % |
提高学习率改善了网络效果,模型收敛速度非常快,但最后出现了过拟合问题,下面使用学习率衰减进行改进。
学习率衰减
更改学习率为0.01,定义每训练3个epoch,学习率衰减至原来的0.2
scheduler = lr_scheduler.StepLR(optimizer, step_size=3, gamma=0.2)
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.0137 | 0.0488 | 98.6 % |
| 多层网络 | 0.0410 | 0.0393 | 98.6 % |
通过学习率衰减的做法,不仅提升了收敛速度,在单层网络中,过拟合有所改善,在多层网络中,几乎消除了过拟合问题,并且对识别准确率也有了改进,两个模型分别提高了1%~2%不等。
(六)参数初始化
torch.nn中对卷积层、全连接层的参数初始化方式在我的前一篇文章正则化与参数初始化对神经网络的影响有介绍。
从那篇文章中可以知道无论是Linear还是Conv2d,其weight参数 w i w_i wi均是利用kaiming_uniform_来初始化的,下面分别将 w e i g h t weight weight初始化方式替换为kaiming_normal_和xavier_normal_,将bias替换为常数0来观察对网络的影响。
kaiming_normal_
kaiming_normal_说明
torch.nn.init.kaiming_normal_(tensor, a=0, mode=‘fan_in’, nonlinearity=‘leaky_relu’)
上述代表以0为均值的正态分布,N~ (0,std),其中std = 2 1 + a 2 × f a n i n \sqrt{\frac{2}{1+a^2×fan_{in}}} 1+a2×fanin2
- a:为激活函数的负半轴的斜率,relu是0
- mode:可选为fan_in 或 fan_out;fan_in在正向传播时,方差一致,fan_out在反向传播时,方差一致
- nonlinearity:可选 relu 和 leaky_relu ,默认值为 leaky_relu
使用下面代码改变模型初始化方式
def weight_init(m):
if isinstance(m, nn.Linear):
nn.init.kaiming_normal_(m.weight)
nn.init.constant_(m.bias, 0)
elif isinstance(m, nn.Conv2d):
nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
# 不断遍历模型的各模块,按照设定进行参数初始化
model_single.apply(weight_init)
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.0072 | 0.0517 | 98.48 % |
| 多层网络 | 0.0660 | 0.0621 | 97.99 % |
使用kaiming_normal_初始化对单层网络改进较大,对多层网络改进较小,但是单层网络训练后期有过拟合的趋势,二者的收敛速度都有较大的提升。
xavier_normal_
xavier_normal_说明
torch.nn.init.xavier_normal_(tensor, gain=1)
根据Glorot, X.和Bengio, Y. 于2010年在《Understanding the diffculty of training deep feedforward neural networks》中描述的方法,用一个正态分布生成值,填充输入的张量或变量。
张量中的值采样自均值为0,标准差为 s t d = g a i n ∗ 2 f a n i n + f a n o u t std=gain*\sqrt{\frac{2}{fan_{in}+fan_{out}}} std=gain∗fanin+fanout2的正态分布。
xavier_normal_也被称为Glorot initialisation.
其中的参数:
- tensor:n维的torch.Tensor
- gain:可选的缩放因子
更改方式与kaiming_normal_相同
| train loss | test loss | acc | |
|---|---|---|---|
| 单层网络 | 0.0107 | 0.0533 | 98.39 % |
| 多层网络 | 0.0663 | 0.0583 | 98.15 % |
与kaiming_normal_的效果相近,对最后准确率有提升,但是单层网络有过拟合趋势。
(七)综合测试
将以上六个操作中对模型改进较大的几个操作进行组合,在多层网络上尝试,改进操作如下
- 添加BN层
- 优化器使用Adam
- 学习率衰减,将学习率设置为0.01,每5个epoch衰减为原来的0.2
- 使用kaiming_normal_初始化参数
- 添加DropOut,设置p=0.5,用于改进过拟合
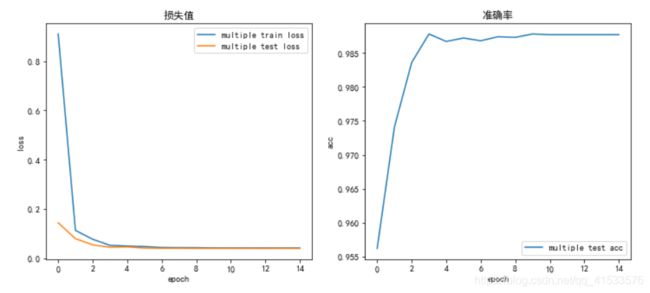
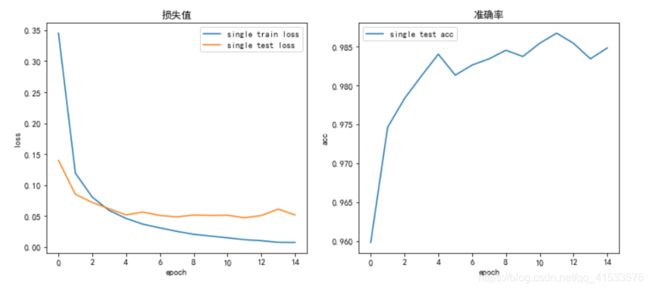
| train loss | test loss | acc | |
|---|---|---|---|
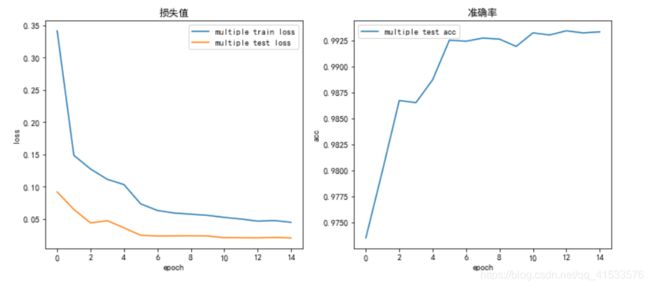
| 多层网络综合测试 | 0.04481 | 0.0214 | 99.33 % |
最后测试准确率上升1.8%,无过拟合,改进效果明显。
一个说明
validation loss 小于 training loss 三个可能原因