本文实例为大家分享了基于numpy实现逻辑回归的具体代码,供大家参考,具体内容如下
交叉熵损失函数;sigmoid激励函数
基于numpy的逻辑回归的程序如下:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets.samples_generator import make_classification
class logistic_regression():
def __init__(self):
pass
def sigmoid(self, x):
z = 1 /(1 + np.exp(-x))
return z
def initialize_params(self, dims):
W = np.zeros((dims, 1))
b = 0
return W, b
def logistic(self, X, y, W, b):
num_train = X.shape[0]
num_feature = X.shape[1]
a = self.sigmoid(np.dot(X, W) + b)
cost = -1 / num_train * np.sum(y * np.log(a) + (1 - y) * np.log(1 - a))
dW = np.dot(X.T, (a - y)) / num_train
db = np.sum(a - y) / num_train
cost = np.squeeze(cost)#[]列向量,易于plot
return a, cost, dW, db
def logistic_train(self, X, y, learning_rate, epochs):
W, b = self.initialize_params(X.shape[1])
cost_list = []
for i in range(epochs):
a, cost, dW, db = self.logistic(X, y, W, b)
W = W - learning_rate * dW
b = b - learning_rate * db
if i % 100 == 0:
cost_list.append(cost)
if i % 100 == 0:
print('epoch %d cost %f' % (i, cost))
params = {
'W': W,
'b': b
}
grads = {
'dW': dW,
'db': db
}
return cost_list, params, grads
def predict(self, X, params):
y_prediction = self.sigmoid(np.dot(X, params['W']) + params['b'])
#二分类
for i in range(len(y_prediction)):
if y_prediction[i] > 0.5:
y_prediction[i] = 1
else:
y_prediction[i] = 0
return y_prediction
#精确度计算
def accuracy(self, y_test, y_pred):
correct_count = 0
for i in range(len(y_test)):
for j in range(len(y_pred)):
if y_test[i] == y_pred[j] and i == j:
correct_count += 1
accuracy_score = correct_count / len(y_test)
return accuracy_score
#创建数据
def create_data(self):
X, labels = make_classification(n_samples=100, n_features=2, n_redundant=0, n_informative=2)
labels = labels.reshape((-1, 1))
offset = int(X.shape[0] * 0.9)
#训练集与测试集的划分
X_train, y_train = X[:offset], labels[:offset]
X_test, y_test = X[offset:], labels[offset:]
return X_train, y_train, X_test, y_test
#画图函数
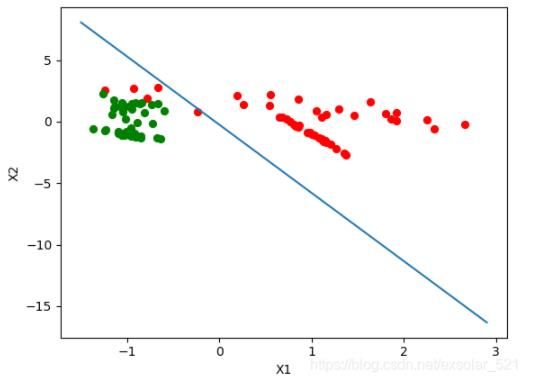
def plot_logistic(self, X_train, y_train, params):
n = X_train.shape[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if y_train[i] == 1:#1类
xcord1.append(X_train[i][0])
ycord1.append(X_train[i][1])
else:#0类
xcord2.append(X_train[i][0])
ycord2.append(X_train[i][1])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=32, c='red')
ax.scatter(xcord2, ycord2, s=32, c='green')#画点
x = np.arange(-1.5, 3, 0.1)
y = (-params['b'] - params['W'][0] * x) / params['W'][1]#画二分类直线
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
if __name__ == "__main__":
model = logistic_regression()
X_train, y_train, X_test, y_test = model.create_data()
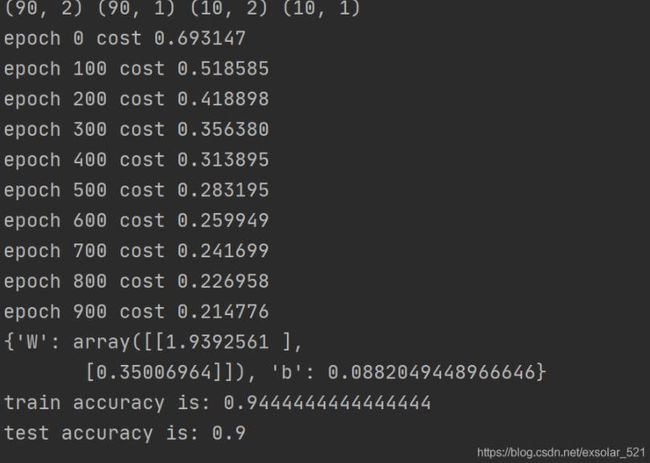
print(X_train.shape, y_train.shape, X_test.shape, y_test.shape)
# (90, 2)(90, 1)(10, 2)(10, 1)
#训练模型
cost_list, params, grads = model.logistic_train(X_train, y_train, 0.01, 1000)
print(params)
#计算精确度
y_train_pred = model.predict(X_train, params)
accuracy_score_train = model.accuracy(y_train, y_train_pred)
print('train accuracy is:', accuracy_score_train)
y_test_pred = model.predict(X_test, params)
accuracy_score_test = model.accuracy(y_test, y_test_pred)
print('test accuracy is:', accuracy_score_test)
model.plot_logistic(X_train, y_train, params)
结果如下所示:
以上就是本文的全部内容,希望对大家的学习有所帮助,也希望大家多多支持脚本之家。