GraphSAGE的一些理解以及一些模块的DGL的代码实现

前言

因为参加天池比赛，要求最好使用纯inductive的模型，一脸懵逼，inductive是什么，后来搜了才知道，还有transductive模型，具体区别就是，transductive是只能够用于已知的图结构，而inductive可以用于未知的图结构，我们平时所用的模型一般都是inductive的，最原始的GCN通过节点的度来确定权重训练需要使用到图结构，那么换了个新的图就不适用了，而GraphSAGE是通过训练出一个“采样聚合器”，不依赖原本的图结构，那么便可以直接用在新图里了（我目前理解是这样，要有不妥，以后再来改）

GraphSAGE

传播公式

GraphSAGE的更新embedding的思路非常简单：

首先确定一个需要更新的节点。

然后找出这个节点的所有邻居节点，然后将邻居节点的信息进行聚合（取均值、求和等方式）得到邻居的特征。

最后将此节点的原特征和求得的邻居特征进行拼接进行线性变换再激活一下等操作得到此节点更新之后的特征。

可以举个例子：

例如我们需要求1节点更新后的特征，我们可以看到1节点的邻居节点为3，4，5，6节点，那么可以聚合1节点邻居节点的特征，这里采用的是均值，即求特征对应维度的平均值作为聚合邻居的特征，然后和1节点的特征进行拼接再进行线性变换和激活得到更新后的1节点的特征。

邻居采样

因为GraphSAGE需要聚合节点的邻居信息，那么取多少个邻居节点呢？如果所有邻居都取的话势必会增加算法的复杂度，因此此文章的作者提出固定邻居采样的数量S，如果节点邻居的数量>S，则从中随机抽取S个邻居，如果节点邻居小于S，则重复采样邻居节点到S时结束。

同时，文章指出，当采样两层，且第一层采样邻居数S1 * 第二次层采样邻居数S2 <= 500会有比较好的效果。

举个例子：

假设只采样一层，采样数S1 = 3
对于1节点有2，3，5，6四个节点的边指向它，即有四个邻居，那么进行邻居采样就是从四个中随机抽三个出来进行聚合；对于2节点，它的邻居为1，3，取了所有的邻居还不够，那么再在1，3中随机抽取一个凑齐3个再进行聚合。

聚合函数

聚合函数就是用于聚合邻居特征，简单来说就是通过一个聚合出表达出邻居的特征，对于输入排列不变的聚合函数都可以适用。

对于LSTM文章提到说它比mean操作更好，因为有更大的容量，因为邻居数量并不多，可以说LSTM将邻居的特征都记住了？

minbatch

我们都知道，最开始的GCN是直接将整张图直接进行特征更新的，那么整张图的大小很容易就超过了一块GPU的大小，使得大图不容易进行训练，那么邻居采样的思路可以让大图的训练变得简单，我们可以确定更新的节点然后采样出所需要的邻居，然后将这一块小图放在GPU上即可完成此节点的更新，这样一来，大图可以拆成若干小图，就算是超大的图也能够轻而易举的进行训练了。

举个例子：

例如K=2 S1 = 3, S2 = 2
表示取两层邻居更新节点，第一层邻居取3个，第二层邻居取2个，假设我们要更新节点a，第一层从b，c，f，j中任意取三个节点作为邻居节点，这里取了j，f，c三个，然后这三个节点再任意取两个邻居更新节点的信息，最后更新a节点的信息，这样更新a节点的信息只需要图中的一块即可，不需要将整张图放到GPU上。

DGL实现邻居采样

我感觉GraphSAGE最重要的就是邻居采样这部分吧，聚合那块还是比较简单的，因此下面将着重解释和用DGL实现邻居采样。

同构图

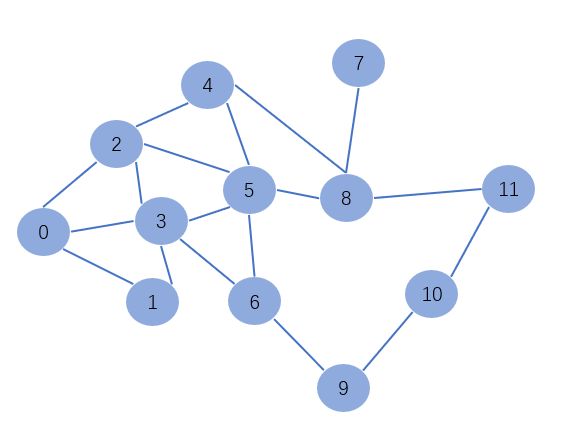
首先可以构建这么一张同构图，然后调调参数可能就懂那些参数是什么意思了吧，调试代码如下：

import torch
import dgl

src = torch.LongTensor(
    [0, 0, 0, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 10,
     1, 2, 3, 3, 3, 4, 5, 5, 6, 5, 8, 6, 8, 9, 8, 11, 11, 10, 11])
dst = torch.LongTensor(
    [1, 2, 3, 3, 3, 4, 5, 5, 6, 5, 8, 6, 8, 9, 8, 11, 11, 10, 11,
     0, 0, 0, 1, 2, 2, 2, 3, 3, 4, 4, 5, 5, 6, 7, 7, 8, 9, 10])
g = dgl.graph((src, dst))

sampler = dgl.dataloading.NeighborSampler([1, 2, 3])
dataloader = dgl.dataloading.DataLoader(
    g, [5], sampler,
    batch_size=1, shuffle=True, drop_last=False, num_workers=4)
for input_nodes, output_nodes, blocks in dataloader:
    print(input_nodes) # 输入的节点数
    print(output_nodes) # 输出的节点数
    print(blocks)
    for i in range(len(blocks)):
        left, right = blocks[i].edges()
        u = [int(input_nodes[l]) for l in left]
        v = [int(input_nodes[r]) for r in right]
        print("u_v", u, v)
        print("此块输入节点", blocks[i].srcdata)
        print("此块输出节点", blocks[i].dstdata)
        print("*" * 10)
    print("="*10)

输出（随机一次）：

sampler = dgl.dataloading.NeighborSampler([1, 2, 3])

可见sampler就是在规定每层邻居的采样数量，第一层为1，第二层为2，第三层为3，每层采样的邻居对应一层gnn需要计算的所有节点，因此这里3个block就对应着三层gnn计算5号节点的所有节点了，这样就能够进行minbatch训练了。

异构图

对于异构也是一样：

假如有那么一副异构图，u表示user，g表示game，s表示store，不同的颜色表示不同的节点，不同的关系也用不同的颜色表示。

代码如下：

import dgl
import torch
import dgl
g = dgl.heterograph({
    ('user', 'follows', 'user') : ([0, 1, 2, 3, 3, 4], [1, 2, 1, 1, 4, 0]),
    ('user', 'plays', 'game') : ([0, 1, 1, 2], [1, 1, 2, 3]),
    ('store', 'sells', 'game')  :([0, 0, 2, 3, 5], [2, 1, 2, 3, 4]),
    ("game", "absorbed", "user") : ([1, 2], [1, 1]),
    ("store", "bought", "user") : ([3], [1])})

sampler = dgl.dataloading.NeighborSampler([1, 1])
dataloader = dgl.dataloading.DataLoader(
    g, {"user":torch.tensor([1])}, sampler,
    batch_size=1, shuffle=True, drop_last=False, num_workers=4)
for input_nodes, output_nodes, blocks in dataloader:
    print(input_nodes)
    print(output_nodes)
    for i in range(len(blocks)):
        print("此块输入节点", blocks[i].srcdata)
        print("此块输出节点", blocks[i].dstdata)
        print("*" * 10)
    print("="*10)
    print(blocks)

输出结果：

我们可以看到，虽然是

sampler = dgl.dataloading.NeighborSampler([1, 1])

但是最后一层却有3 + 1（u1自身）共4个节点的输入，但是仔细想想，异构图的话，那应该是每种关系的邻居取1，这样看来，确实如此。

如果我们需要对不同的关系设定不同的采样数量，也是可以的，代码如下：

import dgl
import torch
import dgl
g = dgl.heterograph({
    ('user', 'follows', 'user') : ([0, 1, 2, 3, 3, 4], [1, 2, 1, 1, 4, 0]),
    ('user', 'plays', 'game') : ([0, 1, 1, 2], [1, 1, 2, 3]),
    ('store', 'sells', 'game')  :([0, 0, 2, 3, 5], [2, 1, 2, 3, 4]),
    ("game", "absorbed", "user") : ([1, 2], [1, 1]),
    ("store", "bought", "user") : ([3], [1])})

sampler = dgl.dataloading.NeighborSampler([
    {('user', 'follows', 'user'): 2,  # follows关系采样2个
    ('user', 'plays', 'game'):1,
    ('store', 'sells', 'game'):1,
    ("game", "absorbed", "user"):1,
    ("store", "bought", "user"):1}] * 2)
dataloader = dgl.dataloading.DataLoader(
    g, {"user":torch.tensor([1])}, sampler,
    batch_size=1, shuffle=True, drop_last=False, num_workers=4)
for input_nodes, output_nodes, blocks in dataloader:
    print(input_nodes)
    print(output_nodes)
    for i in range(len(blocks)):
        print("此块输入节点", blocks[i].srcdata)
        print("此块输出节点", blocks[i].dstdata)
        print("*" * 10)
    print("="*10)
    print(blocks)

输出：

我们可以看到，最后一层user确实是（3-1）2个邻居节点传来。

总结

本来想画个图来展现一层层采样的汇聚过程的，但是感觉好像有点过于复杂了，那就直接从最后一步的结果来理解也是可以的吧，DGL邻居采样能够根据gnn的层数来得出对应得结果，计算的时候，只需要对应得block参与对应层gnn计算即可，这样实现了minbatch的计算，使得超大图得以轻松的训练。

参考

https://www.bilibili.com/video/BV1K5411H7EQ?p=10&vd_source=f57738ab6bbbbd5fe07aae2e1fa1280f

Inductive Representation Learning on Large Graphs

https://docs.dgl.ai/guide_cn/minibatch-custom-sampler.html