机器学习：基于聚类K-Means算法实现图像的分割研究

目录

摘要

序言

图像分割实验：

1、实验步骤

 2、程序代码

3、实验数据

4、实验总结及分析

总结

---

摘要

在一幅图像中,景物往往有众多的目标组成，反映在图像中是众多的区域。图像分割属于图像处理中一种重要的图像分析技术。图像分割的传统方法是对灰度图像分割，处理图像的亮度分量，简单快速。但却忽略了图像中很大一部分信息:色彩，因此分割效果不佳。对彩色图像分割的研究一直是图像处理的焦点，它采用各种颜色空间模型，使得图像分割更全面，更精确。

本文章首先介绍了传统的图像分割与聚类算法分割，然后重点介绍一种基于K-均值聚类算法的图像改进分割方法。实验结果表明，改进的分割方法能够实时稳定的对目标分割提取，分割效果良好。

关键词：K-Means聚类，机器学习，python，聚类算法

序言

在计算机视觉和图像分析中。如何把目标物体从图像中有效分割出来一直是一个经典难题之一，它决定图像的最终分析质量和模式识别的判别结果。图像分割是指将图像中具有特殊意义的不同区域分开来,并使这些区域相互不相交,且每个区域应满足特定区域的一致性条件。图像一旦被分割，就可作进-步的处理，如基于内容的图像检索、分类及识别等。因此，图像分割是图像处理和模式识别中的一个重要研究领域。目前图像分割的算法主要有阈值分割法、边缘提取法、区域分割法、分水岭分割法等，这些分割算法各有优缺点。近年来，许多研究人员提出用聚类算法来分割图像，并取得了较好的实验结果。但如何初始划分(分类)样本以及选择代表点将直接影响分割的效果。在以往的研究中，基于K均值聚类及其改进算法的图像分割技术受到了广泛关注。

图像分割综述

21世纪是信息化的时代，信息的形式不再是单纯的语音，而是发展到包括数据、文字、图像、视频等在内的多媒体形式。据统计，人类接受外界的信息中有80%来自图像。图像分割技术是针对性很强的技术，它在人类生产和生活的方方面面起到了越来越重要的作用。

图像分割技术的现状和发展情况

图像分割算法的研究已有几十年的历史，一直以来都受到人们的高度重视。关于图像分割的原理和方法国内外已有不少的论文发表,但一直以来没有一种分割方法适用于所有图像分割处理。传统的图像分割方法存在着不足，不能满足人们的要求，为进一步的图像分析和理解带来了困难。

图像分割主要研究方法

图像分割是图像处理中的一项关键技术，图像分割是把图像分割成若干个特定的、具有独特性质的区域并提取出感兴趣目标的技术和过程，这些特性可以是像素的灰度、颜色、纹理等提取的目标可以是对应的单个区域，也可以是对应的多个区域。图像分割方法有许多种分类方式，在这里将分割方法概括为四类:边缘检测方法、区域生长方法、阈值分割方法及结合特定理论工具的分割方法。

聚类概念

将物理或抽象对象的集合分成由类似的对象组成的多个类的过程被称为聚类。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象彼此相似，与其他“簇”中的对象相异。聚类分析又称“群分析”，它是研究(样品或指标)分类问题的一种统计分析方法。聚类分析计算方法主要有如下几种：划分方法，层次方法，基于密度的方法，基于网格的方法,基于模型的方法。

K-均值聚类算法是著名的划分聚类分割方法。划分方法的基本思想是:给定一个有N个元组或者纪录的数据集，分裂法将构造K个分组，每一个分组就代表一个聚类。而且这K个分组满足下列条件: (1)每一个分组至少包含-一个数据纪录; (2) 每一个数据纪录属于且仅属于一个分组；对于给定的K，算法首先给出一个初始的分组方法，以后通过反复迭代的方法改变分组，使得每一次改进之 后的分组方案都较前-次好，而所谓好的标准就是：同一分组中的记录越近越好，而不同分组中的纪录越远越好。

K-均值聚类算法

k-Means算法是machine learning领域

聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。聚类中心以及分配给它们的对象就代表一个聚类。一旦全部对象都被分配了，每个聚类的聚类中心会根据聚类中现有的对象被重新计算。这个过程将不断重复直到满足某个终止条件。

K-均值聚类算法描述

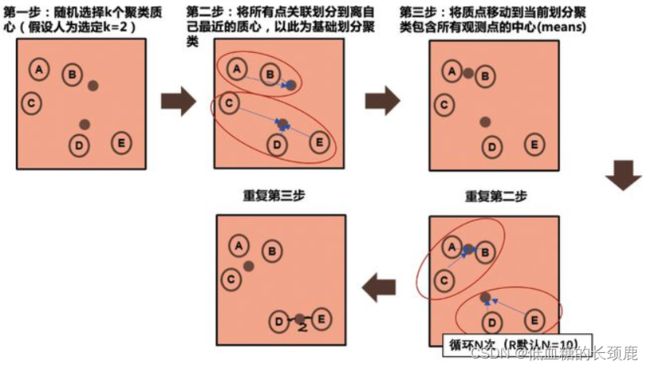
• 随机选取聚类中心。
• 根据当前聚类中心，利用选定的度量方式，分类所有样本点。
• 计算当前每一类的样本点的均值，作为下一次迭代的聚类中心。
• 计算下一次迭代的聚类中心与当前聚类中心的差距，如若差距小于迭代阈值时，迭代结束。

K-均值聚类算法描述图（如下图所示）

K-均值聚类算法代码轮廓：

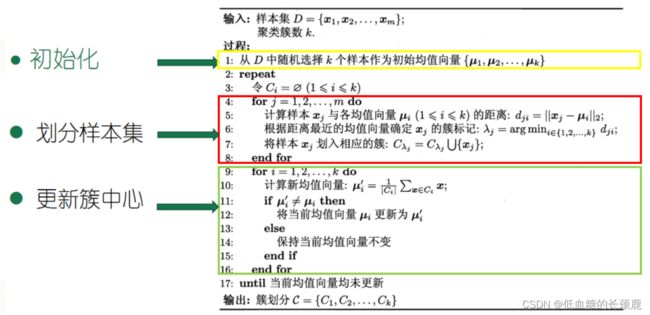
    输入：样本集D={x1,x2,…,xn};

          聚类簇数k

    过程：从样本集D中随机选择k个样本作为初始均值向量{u1,u2,…,uk}

    Repeat

   令Ci = Ø(1≤i≤k)

    for j = 1,2, …,m  do

       计算样本xj与各均值向量ui的距离：dji =||xj-ui||2;

       根据距离最近的均值向量确定xj的簇标记：λj = argminie{1,2,…,k}dji

       将样本xj划入相应的簇：Cλj = Cλj ∪ {xj}

    end for

   for i = 1,2,...,k

    计算新的均值向量：ui' = 1||Ci||

       if ui' ≠ ui then

              将当前均值向量ui更新为ui'

       else

       保持当前均值向量不变

   end if

end for

until 当前均值向量均未更新

输出：“簇”划分C = {C1,C2,…,Ck}

其中，D为样本集，聚类所得“簇”划分为C

K-均值聚类算法代码轮廓图：（如下图所示）

K-均值聚类法在图像分割中得到广泛应用。在K-均值算法中,常规的优化算法主要针对聚类数和聚类中心的选取，即通过一些检测聚类有效性的函数计算最佳聚类数k，并在此基础上优化分割效果。近年的一些研究[10][11]表明，融合多种图像特征更有利于获得较好的分割效果，研究表明，在对自然彩色图像进行分割时，考虑了像素的空间特征，算法有更好的鲁棒性。

图像特征提取

颜色特征的提取

颜色特征是在图像分割中应用最为广泛的视觉特征，在一些算法中，一个高复杂度特征的提取可能能够解决问题（进行目标检测等目的），但这将以处理更多数据，需要更高的处理效果为代价。而颜色特征无需进行大量计算。只需将数字图像中的像素值进行相应转换，表现为数值即可。因此颜色特征以其低复杂度成为了一个较好的特征。

纹理特征的提取

纹理通常指在图像中反复出现的局部模式和它们的排列规则，具有不依赖于颜色或照度并可以反映图像中同质现象的特点,

图像分割实验：

利用图像的灰度、颜色、纹理、形状等特征，把图像分成若干个互不重叠的区域，并使这些特征在同一区域内呈现相似性，在不同的区域之间存在明显的差异性。然后就可以将分割的图像中具有独特性质的区域提取出来用于不同的研究。本次实验我们将apple聚类中心设置n_clusters=3，cat聚类中心设置为2。

1、实验步骤

• 建立kms.py工程并导入所需python包
• 加载本地图片进行预处理
• K-Means聚类算法实现
• 聚类像素点并保存输出

 2、程序代码

import numpy as np
import PIL.Image as image
from sklearn.cluster import KMeans
def loadDate(filePath):
    f=open(filePath,'rb')#以二进制打开文件
    data=[]
    img=image.open(f)#以列表形式储存图片像素值
    m,n=img.size#获得图片大小，为便利每个像素准备
    for i in range(m):
        for j in range(n):
            x,y,z=img.getpixel((i,j))
            #getpixel返回指定位置的像素，如果所打开的图像是多层次的图片，那这个方法就返回一个元组
            data.append([x/256.0,y/256.0,z/256.0])#将每个像素归一化成0-1
    f.close()
    return np.array(data),m,n#返回矩阵形式的data，以及图片的大小

imgData,row,col=loadDate("C:/Users/lenovo/Desktop/cat.jpg")
#使用loadData方法处理图片
label=KMeans(n_clusters=3).fit_predict(imgData)
#聚类获取每个像素所属类别
label=label.reshape([row,col])
#创建一张灰度图保存聚类后的结果
pic_new=image.new("L",(row,col))
#根据所属类别向图片中添加灰度值

for i in range(row):
    for j in range(col):
        pic_new.putpixel((i,j),int(256/(label[i][j]+1)))
pic_new.save("C:/Users/lenovo/Desktop/new_cat.jpg","JPEG")#保存处理后的图片

3、实验数据

测试image：

3、实验结果

结果图1

结果图2

4、实验总结及分析

在本次实验中，利用K-Means算法将图像分割出来，但从结果图来看，效果不是很理想。通过设置不同的聚类中心，从而得到不同的聚类结果。如果想要得到预想的效果，必须多次尝试，这使得K值具有不确定性，不利于操作。实验表明，基于粗糙集理论和K-均值聚类算法的图像分割方法，比随机选取聚类的中心点和个数减少了运算量，提高了 分类精度和准确性，而且对于低对比度、多层次变化背景的图像的形状特征提取具有轮廓清晰、算法运行速度快、内存占用小等特点，是一种有效的灰度图像分割算法。

K-Means聚类算法的主要优点：

（1）原理比较简单，实现也是很容易，收敛速度快。

（2）聚类效果较优。

（3）算法的可解释度比较强。

（4）主要需要调参的参数仅仅是簇数k。

K-Means聚类算法的主要缺点：

（1）K值的选取不好把握

（2）采用迭代方法，得到的结果只是局部最优

（3）对噪音和异常点敏感

（4）初始聚类中心的选择

（5）如果各隐含类别的数据不平衡，比如各隐含类别的数据量严重失衡，或者各隐含类别的方差不同，则聚类效果不佳。

（6）对于不是凸的数据集比较难收敛

总结

将K-均值理论应用在图像分割中，发现K-均值理论在图像分割中具有很高的应用价值。本项目仅用于技术交流和学习，欢迎提出改进意见，以期共同进步。本人也是新手，还望各位大佬可以提出建议，感谢！