Python:机器学习：SVM（SVR）（GA遗传\grid网格）

目录

0 前言（优缺点）

1 了解SVM/SVR

2 了解SVM数学推导

2.1 从低维映射到高维（独特）

2.2 找出w和b

3 了解SVR数学推导

3.1 松弛变量

4 掌握python代码应用

4.1 调节c和g

4.2 核函数的选择

4.3 代码（以茎流为例）

4.3.1 SVR_1:最基本的的流程

4.3.2 SVR_2:加入网格寻优

4.3.3 SVR_3:加入遗传寻优

5 注意事项

---

0 前言（优缺点）

参考部分博客，在此将支持向量机(support vector machine)小结。

下一步学习统计学、相关与回归、时间序列、要开始分析自己的第一批数据。

优点：

1）可以解决高维特征的分类和回归问题

2）模型最终结果无需依赖全体样本，只需依赖支持向量

3）有已经研究好的核技巧可以使用，可以应对线性不可分的问题

4）样本量中等偏小的情况也有较好的效果，有一点泛化能力和鲁棒性。这也是深度学习热门起来之前，SVM比较火的主要原因

缺点：

1）常规的SVM只支持二分类

2）SVM在样本巨大且使用核函数时计算量很大

3）线性不可分数据的核函数选择没有同一标准

4）SVM对缺失数据和噪声数据较为敏感

5）SVM更适合同性质的特征，如连续特征，对特征多样性没有更好支持

---

1 了解SVM/SVR

支持向量机 support vector machine

它是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器

其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。

SVM是分类，即输入不论是几维，输出只有两个选择，毕竟是分类嘛。

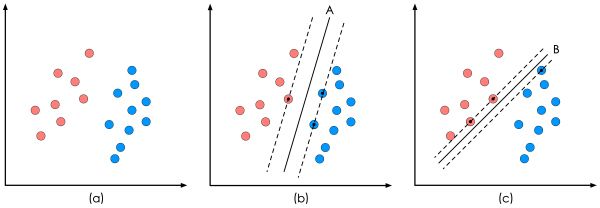
分类任务中，使靠超平面最近的样本点之间的间隔最大；

SVR的R是回归，即输出是连续的，不仅仅是两个选择。

在回归任务中，同样也是看间隔，不同的是使靠超平面最远的样本点之间的间隔最小。

（也就是包含了所有样本点，在两条虚线中间的线就是超平面）

因此，我们的目的就是求出分割线的公式。

---

2 了解SVM数学推导

这条分割线（也叫作超平面），我们暂定为：

求出公式中的w（权重）和b（偏置），是我们的目的。

当f（x）等于0的时候，认为x位于分割线（超平面）上。

---

要把线性可分推广到线性不可分问题。

因为高维空间一定可以线性可分，

因此在高维空间解决线性不可分问题。

即从低维映射到高维

2.1 从低维映射到高维（独特）

构建低维到高维的映射：映射关系

核函数K是与映射关系是一一对应的，核函数在低维进行计算，将实质上的分类结果显示在高维上，避免了直接在高维空间的复杂计算。

2.2 找出w和b

通过原问题与对偶问题等解出w等，SMO算法等

---

3 了解SVR数学推导

SVR的目的是：保证所有样本点在ε管道内的前提下，回归超平面f ( x ) 尽可能地平。

3.1 松弛变量

ε设置太小无法保证所有样本点都在ε 管道内，ε 太大回归超平面会被一些异常点带偏。

---

4 掌握python代码应用

4.1 调节c和g

SVM的超参数C用于调节松弛因子的占比，C越大对错误样本的惩罚越大

（1）低偏差、高方差，即遇到了过拟合时，减少C

（2）高偏差、低方差，即遇到了欠拟合时，增大C

4.2 核函数的选择

（1）当特征维度较高，样本量较少时，不宜使用核函数或者使用线性核的SVM

（2）当特征维度较低，样本量规模大的时候，可以使用高斯核函数，使用前需要对特征进行缩放

总之要看特征维度和样本规模，以免升维后的过拟合

1)线性核函数（linear）

2)多项式核：多项式形式的核函数具有良好的全局性质。局部性较差。

3)径向基核（rbf）：高斯核函数，局部性强的核函数，其外推能力随着参数的增大而减弱。

4)傅里叶核

5)样条核

6)Sigmoid核函数

---

4.3 代码（以茎流为例）

4.3.1 SVR_1:最基本的的流程

1）载入包

2）类（归一化、反归一化、读写函数）

3）main（画图通用、numpy读取csv数据、数据归一化、划分训练和测试集、模型训练、输出决定系数与误差）

---

4.3.2 SVR_2:加入网格寻优

1）载入包

2）类（归一化、反归一化、读写函数）

3）main（画图通用、numpy读取csv数据、归一化、划分训练和测试集（存pkl）、网格法找到最优的cg（存png）、找到最佳的模型（存pkl））

4）重新创建一个 .py文件，不能再划分训练和测试集，用之前得到的最佳模型跑测试集，画图（存png），保证结果的唯一性。

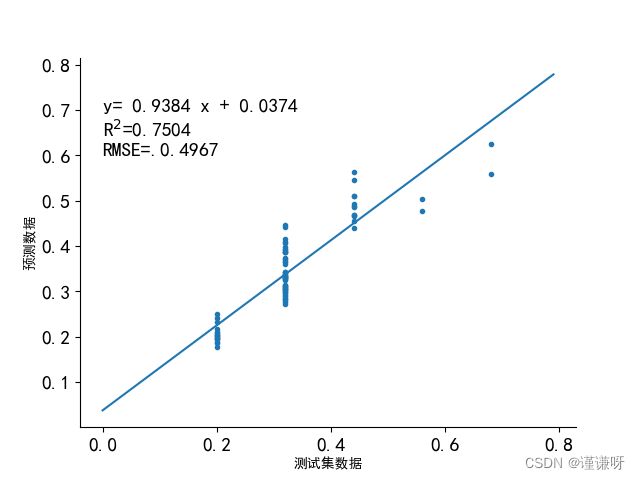
网格法寻优

 

 决定系数仅为0.7504

---

4.3.3 SVR_3:加入遗传寻优

1）载入包

2）类（归一化、反归一化、读写函数）

3）main（画图通用、numpy读取csv数据、归一化、划分训练和测试集（存pkl）、遗传寻法找到最优的cg（存进化流程png）、找到最佳的模型（存pkl））

4）重新创建一个 .py文件，不能再划分训练和测试集，用之前得到的最佳模型跑测试集，画图（存png），保证结果的唯一性。

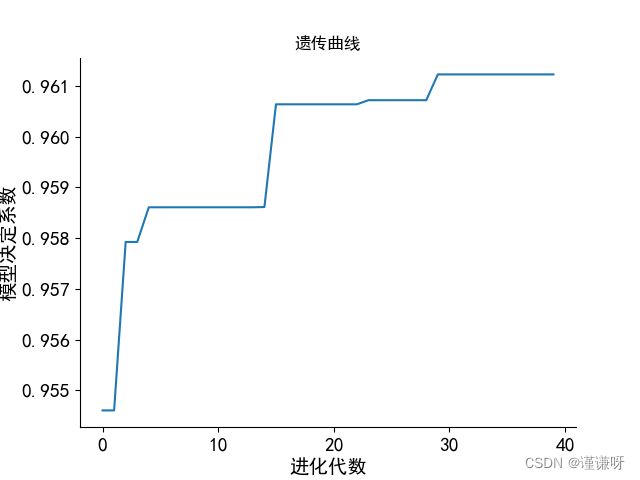
 遗传算法的寻优过程

决定系数为0.9612

---

 

5 注意事项

分割训练集和测试集后，用不同寻优算法在训练集中定下模型的各个参数，保存此模型。随后在测试集上计算其决定系数等指标。