数据结构与算法笔记

1，数据结构

线性表：

非线性表：

• 线性表
  • 数组
  • 链表
    • 单链表
    • 
    • 
    • 双向链表
    • 
    • 循环链表
    • 
    • 双向循环链表
    • 
    • 静态链表
  • 栈：顺序栈、链式栈
  • 队列
    • 普通队列、双端队列
    • 阻塞队列、并发队列、阻塞并发队列
• 散列表
  • 散列函数
  • 冲突解决：链表法、开放寻址
  • 动态扩容
  • 位图
• 树
  • 二叉树
    • 平衡二叉树、二叉查找树
    • 平衡二叉查找树：AVL 树、红黑树
    • 完全二叉树、满二叉树
  • 多路查找树
    • B 树、B+ 树
    • 2-3 树、2-3-4 树
  • 堆
    • 小顶堆、大顶堆
    • 优先级队列、斐波那契堆、二项堆
• 图
  • 图的存储：邻接矩阵、邻接表
  • 拓扑排序、最短路径、关键路径
  • 最小生成树、二分图、最大流

2，算法

• 复杂度分析
  • 空间复杂度
  • 时间复杂度：最好、最坏、平均、均摊
• 基本算法思想
  • 贪心算法、分治算法、动态规划
  • 回溯算法、枚举算法
• 排序
  • O(n^2)：冒泡排序、插入排序、选择排序、希尔排序
  • O(nlogn)：归并排序、快速排序、堆排序
  • O(n)：计数排序、基数排序、桶排序
• 搜索：深度优先搜索、广度优先搜索
• 查找：线性表查找、树结构查找、散列表查找
• 字符串匹配
  • 朴素、KMP
  • Robin-Karp、Boyer-Moore
  • AC 自动机、Trie、后缀数组

3，排序算法

	排序算法	平均时间复杂度	空间复杂度	是否原地排序	是否稳定	是否基于比较
	冒泡	O(n^2)	O(1)	Y	Y	Y
	插入	O(n^2)	O(1)	Y	Y	Y
	选择	O(n^2)	O(1)	Y	N	Y
	希尔	O(n^2)	O(1)	Y	N	Y
递归思想	快排	O(nlogn)	O(1)	Y	N	Y
递归思想	归并	O(nlogn)	O(n)	N	Y	Y
	堆排序	O(nlogn)	O(1)	Y	N	Y
线性排序	桶排序	O(n)		N	Y	N
线性排序	计数排序	O(n)		N	Y	N
线性排序	基数排序	O(n)		N	Y	N

希尔排序是对插入排序的优化。
原地排序算法：指空间复杂度是 O(1) 的排序算法。
稳定性是指：如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间保持原有的先后顺序。

• 冒泡排序、插入排序、选择排序这三种排序算法，时间复杂度都是O(n^2)，比较高，适合小规模数据的排序。
• 归并排序，快速排序这两种排序算，都采用了分治思想，时间复杂度都是O(nlogn)，适合大规模的数据排序。
• 分治思想，顾名思义，就是分而治之，将一个大问题分解成小的子问题来解决。小的子问题解决了，大问题也就解决了。
• 分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想，递归是一种编程技巧。
• 线性排序算法的速度很快，但是它们对要排序的数据的要求非常苛刻。所以一定要注意它们的使用场景。

1，冒泡排序

冒泡排序只会操作相邻的两个数据。

每次冒泡操作都会对相邻的两个元素进行比较，看是否满足大小关系要求，如果不满足就让他两互换。

一次冒泡会让至少一个元素移动到它应该在的位置，重复 n 次，就完成了 n 个数据的排序。

例如对一组数据 [4，5，6，3，2，1] 进行一趟冒泡排序操作是这样的：

整个冒泡过程如下：

冒泡过程还可以优化。

• 当某次冒泡操作已经没有数据交换时，说明已经达到完全有序，不用再继续执行后续的冒泡操作。

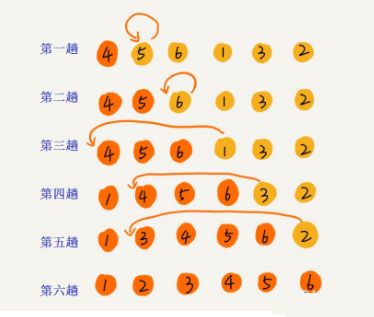
下面的例子有6个元素，只需要4次就可以：

2，插入排序

一个本来有序的数组，在插入一个元素后，使其保持有序。这个过程就相当于插入排序算法的过程。

插入排序算法：

• 首先，将数组中的数据分为两个区，已排序区和未排序区。
• 初始已排序区只有一个元素，就是数组的第一个元素。
• 然后，取未排序区中的元素，在已排序区中找到合适的位置将其插入，并保证已排序区一直有序。
• 重复这个过程，直到未排序区中的元素为空

以数据 [4，5，6，1，3，2] 为例，其中左侧为已排序区间，右侧是未排序区间，其排序过程如下：

3，选择排序

选择排序也分为已排序区和未排序区，每次从未排序区中找到最小的元素，将其放到已排序区的末尾。

4，归并排序

归并排序是一个先分后合的过程。

如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序，再将排好序的两部分合并在一起，这样整个数组就都有序了。

两个有序数组的 merge 过程：

• 申请一个临时数组 tmp，大小与 A[p…r] 相同。
• 用两个游标 i 和 j，分别指向 A[p…q] 和 A[q+1…r] 的第一个元素。比较这两个元素 A[i] 和 A[j]：
  • 如果 A[i] <= A[j]，就把 A[i] 放入 tmp，且将 i 后移一位
  • 如果 A[i] > A[j]，就把 A[j] 放入 tmp，且将 j 后移一位
• 继续上述比较过程，直到其中一个子数组中的所有数据都放入 tmp 中，再把另一个数组中的数据依次放入 tmp 的末尾
• 这时，tmp 就是两个子数组合并之后的结果，最后将 tmp 中的数据拷贝到 A[p…r] 中

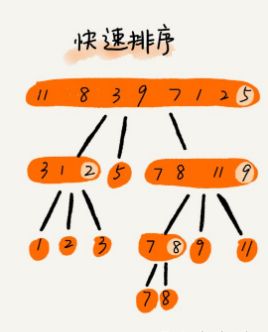
5，快速排序

快排也是利用分治思想。

如果要排序数组中下标从 p 到 r 之间的数据，我们选择 p 到 r 之间的任意一个数据作为 pivot（分区点，一般选择区间中的最后一个），遍历 p 到 r 之间的数据：

• 将小于 pivot 的放到左边
• 将大于 pivot 的放到右边
• 将 pivot 放到中间

那么，p 到 r 之间的数据被分成了三个部分：

• p 到 q-1 之间的都小于 pivot
• 中间是 pivot
• q+1 到 r 之间的都大于 pivot

根据分治、递归思想，可以用递归排序下标从 p 到 p-1 之间的数据和 q+1 到 r 之间的数据，直到区间缩小到 1。

6，通用排序算法

如何实现一个通用的排序算法？

• 线性排序算法虽然时间复杂度低，但其对原数据的要求较高，使用场景较特殊。所以，它不适合用来实现一个通用的排序算法。
• 对于数据规模小的，可以使用 O(n^2) 的排序算法。
• 对于数据量较大的，一般会使用O(nlogn) 算法，所以为了兼顾数据规模一般会选用O(nlogn) 算法。
• O(nlogn) 算法中有归并排序，快速排序，推排序。因为归并排序需要额外的空间，所以归并排序的使用并不多。
• Java 语言的排序使用推排序实现，C 语言的排序使用快速排序实现。

4，查找算法

查找算法	时间复杂度	空间复杂度
有序链表	O(n)	O(1)
二分查找	O(logn)	O(1)
跳表	O(logn)	O(n)
哈希表	O(1)
二叉查找树	O(logn)
红黑树	O(logn)
最大/最小堆	O(logn)	O(1)
图的广度优先搜索	O(V+E)	O(v)
图的深度优先搜索

V是顶点的个数，E是边的个数

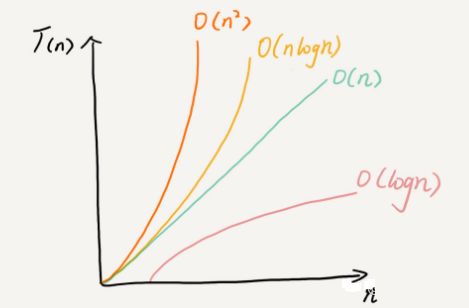
几种常见的复杂度量级

• 常量阶 O(1)
• 对数阶 O(logn)，线性阶 O(n)，线性对数阶 O(nlogn)
• 平方阶 O(n^2)，立方阶 O(n^3)，K 方阶 O(n^k)
• 指数阶 O(2^n)，阶乘阶 O(n!)

1，二分查找

二分查找，针对的是一个有序的数据集，每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。

例子：在 [8，11，19，23，27，33，45，55，67，98] 中查找数字19。

二分查找应用场景的局限性

• 二分查找只使用数组结构，而不能是链表
  • 因为数组查找中间元素的时间复杂度是O(1)
  • 而链表查找中间元素的时间复杂度是O(n)，时间成本会大大增加
• 二分查找只能使用有序数据
  • 如果是无序的数据，需要先排序。排序的时间复杂度是O(nlogn)
  • 所以，如果我们针对的是一组静态的数据，没有频繁地插入、删除，我们可以进行一次排序，多次二分查找。这样排序的成本可被均摊，二分查找的边际成本就会比较低
  • 如果数据的插入，删除比较频繁，要想使用二分查找，就需要维护一个有序的数组，这样的成本是比较高的。对于动态的数据集合，为了快速查找，二叉树是更好的选择
• 数据量太小时不太适合二分查找，这时普通的顺序查找也行
• 数据量太大是也不适合，因为二分查找需要一个数组结构，而数组结构要求连续的内存空间
  • 如果数据有1G，那寻找一个连续的1G 的内存空间是一个比较苛刻的条件

2，跳表

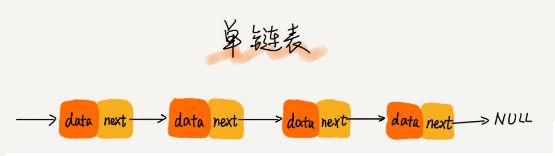
之前讲的二分查找都是基于数组结构，如果数据存储在链表中，而非数组中，需要对链表稍加改造，就可以支持二分查找。这种改造后的数据结构就是跳表。

跳表基于有序链表（可以很好的支持范围查找），是一种各个方面都比较优秀的动态数据结构，可以支持快速的插入，删除，查找操作，实现起来也不复杂，甚至可以替代红黑树。

对于有序的单链表来说，查找一个元素只能从头到尾挨个查找，时间复杂度是O(n)。

为了使链表支持更快的查找，可以为链表建立“索引”，每两个节点向上一级抽取一个节点，这一级称为索引层。索引层使用down 指针指向原始链表。

当查找一个节点的时候，先从索引层查找，再到原始链表查找，这样可以提高速度。

如果再向上抽取一层，如下：

当数据量比较大的时候，跳表可以明显的提高单链表的查找速度。

3，哈希表

哈希表是数组的一种扩展，依赖数组下标的随机访问，没有数组就没有哈希表。

哈希表用的就是数组支持按照下标随机访问的时候，时间复杂度是 O(1) 的特性。

哈希函数

哈希函数设计的基本要求：

• 散列函数计算得到的散列值是一个非负整数
• 如果 key1 = key2，那 hash(key1) = hash(key2)
• 如果 key1 ≠ key2，那 hash(key1) ≠ hash(key2)

对于第3个要求，实际上是不可能实现的。即便像业界著名的MD5、SHA、CRC等哈希算法，也无法完全避免这种散列冲突。另外数组的存储空间有限，也会大大增加哈希冲突的可能性。

哈希算法

将任意长度的二进制值串映射为固定长度的二进制值串，这个映射的规则就是哈希算法，而通过原始数据映射之后得到的二进值串就是哈希值。

哈希算法满足的四点要求：

• 从哈希值不能反向推导出原始数据
• 对数据非常敏感，即使原始数据只修改了一个 Bit，得到的哈希值也不同
• 哈希冲突的概率要很小
• 哈希算法的执行效率要高效

MD5 算法就是一种哈希算法，哈希值是固定的128位二进制串，也就是32位字符串。其最多能表示 2^128 个数据。

// 当多于这个数的时候，md5 值就会发生冲突，已经是天文数字了
2^128 = 340282366920938463463374607431768211456

下面两个串的哈希值就是相同的：

装载因子

• 装载因子 = 填入表中的元素个数 / 散列表的长度

• 装载因子越大，说明空闲位置越少，冲突越多，散列表的性能会下降

• 当装载因子过大时，就需要对哈希表进行动态扩容

  • 假如新申请的空间是之前的两倍，那么扩容后的装载因子就会比之前缩小两倍。
  • 哈希表的扩容，会将数据从老表迁移到新表，因为表的大小变了，所以数据的位置也会变。

• 当动态因子过小时，为避免空间浪费，也可以缩容

解决哈希冲突的办法

• 开放寻址法：如果发生冲突，就再找一个空闲位置，比如：

  • 线性探测：每次将下标 +1，+2，+3，+4，+5 ... 。即从当前位置依次往后查找，实际上问题比较大。
  • 二重探测：每次将下标 +1^2，+2^2，+3^2 ... 。都是加平方。
  • 双重探测
  • 
  • 适合数据量比较小的场景

• 链表法：比较常用，每个桶都对应一个链表

  • 链表法可以使用跳表或红黑树，来使得效率更高
  • 

Java 中 LinkedHashMap 就采用了链表法解决冲突，ThreadLocalMap 是通过线性探测的开放寻址法来解决冲突。

工业级哈希表（Java HashMap）分析

• 初始大小默认值是16，可以设置。
• 最大装载因子默认是 0.75，当表中元素大于 0.75*capacity 时，会扩容为原来的2倍
• 在JDK1.8 中，当链表的长度超过 8 时，链表会转化为红黑树，当长度低于 8 时，又会转回链表
• 哈希函数，简单高效，分布平均

4，二叉查找树

什么是树形结构

• A 节点是 B 节点的父节点
• B 节点是 A 节点的子节点
• B、C、D 互为兄弟节点
• 没有父节点的节点为根节点（E 节点）
• 没有子节点的节点为叶节点（G）

几个概念：

• 节点的高度：节点到叶节点的最长路径（边数）
• 节点的深度：根节点到这个节点的边的个数
• 节点的层数：节点的深度 + 1
• 数的高度：根节点的高度

二叉树

• 二叉树：每个节点最多有两个子节点，分别是左子节点和右子节点
  • 二叉树并不要求每个节点都有两个子节点，有的节点只有左子节点，有的节点只有右子节点
• 满二叉树：叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点
• 完全二叉树：叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，除了最后一层，其他层的节点个数都要达到最大

二叉树的存储方法

• 链式存储法
• 数组存储法

二叉树的遍历

二叉树遍历的时间复杂度是 O(n)。

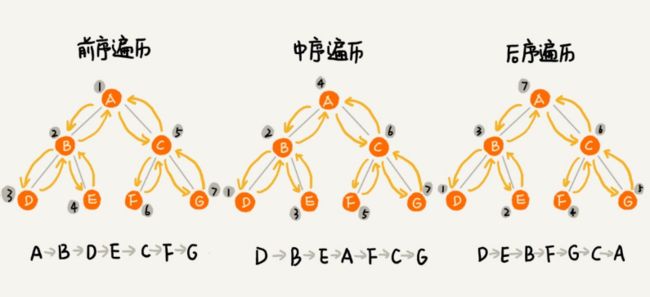
• 前序遍历（根节点在前）：根节点->左子树->右子树
• 中序遍历（根节点在中）：左子树->根节点->右子树
  • 中序遍历时，输出的是顺序序列。所以二叉树又叫二叉排序树。
• 后续遍历（根节点在后）：左子树->右子树->根节点

伪代码如下：

// 前序遍历
void preOrder(Node* root) {
  if (root == null) return;
  print root // 此处为伪代码，表示打印 root 节点
  preOrder(root->left);
  preOrder(root->right);
}

// 中序遍历
void inOrder(Node* root) {
  if (root == null) return;
  inOrder(root->left);
  print root // 此处为伪代码，表示打印 root 节点
  inOrder(root->right);
}

// 后续遍历
void postOrder(Node* root) {
  if (root == null) return;
  postOrder(root->left);
  postOrder(root->right);
  print root // 此处为伪代码，表示打印 root 节点
}

二叉查找树

二叉查找树最大的特点就是，支持动态数据集合的快速插入、删除、查找操作。对于任意一个节点：

• 其左子树中的每个节点的值，都要小于这个节点的值
• 而右子树节点的值都大于这个节点的值

二叉查找树的查找过程：

5，红黑树

平衡二叉树

二叉查找树在极端情况下，时间复杂度会退化到O(n)，所以出现了平衡二叉树。

• 平衡二叉树中任意一个节点的左右子树的高度相差不能大于1。
• 完全二叉树、满二叉树其实都是平衡二叉树，非完全二叉树也有可能是平衡二叉树。
• AVL 树是一种高度平衡的二叉树，红黑树并不是严格意义上的平衡树。

红黑树

红黑树是一颗二叉搜索树，它在每个节点上增加了一个存储位来表示节点的颜色，可以是黑或红。

通过对任何一条从根到叶子的简单路径上各个节点的颜色进行约束，红黑树确保没有一条路径会比其他路径长出 2 倍，因而是近似平衡。

树中每个节点包含 5 个属性：color，key，left，right，p。

红黑树的定义：

• 红黑树中的每个节点都有颜色，红色或黑色
• 根节点是黑色
• 每个叶子节点是黑色的空节点（NIL），叶节点不存储数据
• 任何相邻的节点不能同时为红色（可同时为黑色），红色节点是被黑色节点隔开的
• 每个节点，从该节点到其所有后代叶节点的路径，都包含相同数目的黑色节点

红黑树的优点：

• 红黑树避免了极端情况下性能退化的问题，因为它是一颗近似平衡的树。
• 红黑树不像 AVL 树那样是严格的平衡树，避免了插入，删除操作时对树进行过多的平衡操作。
• 综合来说，红黑树的各项性能都是比较优越的，也是比较稳定的。

6，堆

什么是堆 ？

• 堆是一棵完全二叉树：除了最后一层，其它层的节点个数都是满的，最后一层的节点都靠左排列
• 堆中的每个节点的值都必须大于等于（或小于等于）其子树中每个节点的值
  • 大顶堆：堆中的每个节点的值都大于等于其子树中每个节点的值
  • 小顶堆：堆中的每个节点的值都小于等于其子树中每个节点的值

用数组存储堆

堆可以用数组来实现。

注：文中图片引自《数据结构与算法》