【MCM2015】Ebola's Funeral

美赛自觉发挥不太好，但是上天很眷顾，还是给了个M奖~这才敢把成品发上来，若有不足求轻拍~

 

2015 Mathematical Contest in Modeling (MCM) Summary Sheet
(Attach a copy of this page to your solution paper.)

 

Type a summary of your results on this page. Do not include
the name of your school, advisor, or team members on this page.

Summary

Nowadays, the Ebola outbreak in Western Africa is rigorous. The world medical association has announced that their new medication could stop Ebola and cure patients whose disease is not advanced. To optimize the eradication of Ebola, or at least its current strain, the paper establishes the FPIF (Forecast, Planning, Implementation, Feedback) dynamic model.

Our FPIF model forecasts the spread of the Ebola and determines the optimization scheme of manufacturing, delivery and distribution through the optimization model including three sub-models. And feedback after implementation can be seen as a process of data collection and model parameter adjustment.

Firstly, based on traditional SIQR model, our Ebola spread model not only includes the analysis of therapeutic effect of drugs and vaccines, but also takes integrity and localness relationships between nodes into account.

The pharmaceutical factory produces two kinds of medicine: vaccines and drugs. In the second sub-model, medicine production rate is determined by production equipment investment, production funds and drug demand. By balancing production ratio and the investment ratio of vaccine and drug, the model can obtain the optimal medicine production rate.

As for the delivery system, the third sub-model divides the target region and establishes a space hierarchical structure with layers and nodes. In each layer, we use the shortest path algorithm and calculate each nodes' weighted value of time and cost to determine the transfer station and the delivery system.

To validate the model, a general simulation was made on the basis of simulations of three sub-models. For the reality, we carried out data fitting on collected realistic data using universal global optimization (UGO) algorithms with 1stOpt to get parameters. We get the situation of the epidemic control by Matlab.

Finally, the paper conducts sensitivity analysis, and analyzes the advantages and disadvantages of the model.

 

Ebola's Funeral

Contents

1    Introduction    2

2    Assumptions    2

3    Notations    3

4    Model Overview    5

5    Part1: The Spread of the Disease    6

5.1    The establishment of the model    6

5.2    Preliminary test of the model    9

6    Part2: Speed of Manufacturing of the Vaccine or Drug    11

6.1    The establishment of the model    11

6.2    Preliminary test of the model    13

7    Part3: The Quantity of the Medicine Needed    15

8    Part4: Delivery Systems    16

8.1    The establishment of the model    16

8.2    The simulation of the model    19

8.3    To Further Illustrate the Model    18

9    Supplementary Note    18

10    The General Simulation of the Model    19

11    Future Improvements    22

11.1    The Investment of Health Organizations    22

11.2    Transportation System of Multiple Pharmaceutical Factories    23

11.3    The Production and Distribution of A Variety of Vaccines, Drugs    23

12    Sensitivity Analysis    23

13    Conclusions    25

14    Strengths and Weaknesses    25

14.1    Strengths    25

14.2    Weaknesses    26

A letter for the world medical association    27

References    28

 

 

 

1. Introduction

Ebola is a potent infectious virus that can cause humans and primates to get Ebola hemorrhagic fever, and it also causes a high mortality rate, between 50-90% [1].

The most common way of EVD human transmission is due to contacts with blood or bodily fluids from an infected person (including dead person) or by contact with contaminated fomites (e.g., agriculture material) [1][2].

Regarding the situation, there is a need of development of decision tools to help the authorities to focus their efforts in important factors that can help to eradicate Ebola. Mathematical modeling and, more precisely, epidemiological modeling can help to predict the possible evolution of the Ebola outbreaks and to give some recommendations in the region to be prioritized for surveillance. In our work, under the circumstance that the world medical association has announced that their new medication could stop Ebola and cure patients whose disease is not advanced, we conclude four sub-problems to tackle in our paper to help the world medical association to eradicate Ebola.

• Model building of the spread of the EVD
• Model building of the speed of manufacturing of the vaccine or drug
• Calculating the quantity of the medicine needed, including the medicine that can cure patients whose disease is not advanced and the vaccines for immunization
• Model building of delivery systems and locations of the medicine

In the whole modeling process, we give full consideration to realism, rationality, and usefulness of our model.

1. Assumptions

To simplify the problem, we make the following basic assumptions, each of which is properly justified.

• The total number of people in the model keeps unchanged, That is to say, no migration and the birth of the population.
• The incubation period is not considered, because the incubation period is not infectious [2].
• Assuming that before being injected with the vaccine, all people are susceptible.
• Medicine only for slightly infected people, and can cure all who have had the medicine.
• The vaccine only for those not infected, and will no longer be infected once vaccination.
• In the base model, assuming that there is only one manufacturer, and only a kind of vaccines and drugs.
• In the paper, we view a week as the unit, and ignore the delay of transportation, namely distribution directly after production. Because the shipping time is relatively short when compared to a week.

1. Notations

All the variables and constants used in this paper are listed in the table below.

Symbol	Definition
	The proportion of the total number of susceptible individuals in the number i area
	The proportion of the total number of people infected but not isolated people in the number i area
	The proportion of the total number of people isolated and can be cured people in the number i area
	The proportion of the total number of people isolated and can't be cured people in the number i area
	The proportion of the total number of recovery or death people in the number i area
λ	The average number of people contacted effectively per patient per week
	Contact rate coefficient between i and j
	The ratio of translation from I to
	The ratio of translation from I to
	The ratio of translation from to
	The number of people vaccinated per week in the number i area
	The ratio of translation from I to
	The ratio of translation from to
	The ratio of translation from to
	The population density of the number i area
	The number of people cured by the drugs per week in the number i area
	The initial number of people in the number i area
	The required amount of vaccines for everyone to get immune function

 

	The required amount of drugs, for everyone to be cured
A	The amount of vaccines supplied per week
B	The amount of medicine supplied per week
d	Reference density distribution

 

1. Model Overview

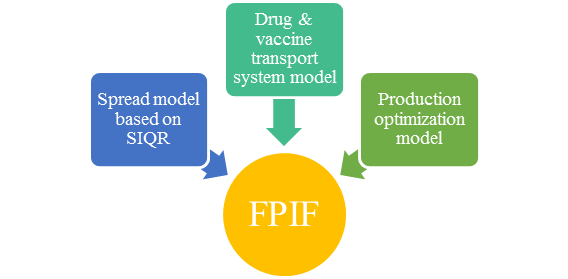
Based on several research aspects including the spread of the Ebola, the quantity of the medicine needed in different areas, possible feasible delivery systems, locations of delivery, speed of manufacturing of the vaccine or drug and money account of the world health organization spent, this paper establish FPIF (Forecast, Planning, Implementation, Feedback) dynamic model, which optimize the eradication of Ebola, or at least its current strain.

The optimization model is divided into three sub models: Ebola spread model based on SIQR, hierarchical medicine delivery system model and medicine manufacturing optimization model.

In practical application, the target region should be divided into layers first. Then, we forecast the spread of the Ebola on the basis of the current epidemic situation, the demand for medicine, the current manufacturing capacity and capital investment, and determine the optimization scheme of manufacturing, delivery and distribution. Thus, according to the optimization scheme, we arranged for manufacturing of the vaccine or drug in the next phase, implement the distribution plan and construction delivery systems. After the implementation, we report the feedback back to the model, and continue the next phase of the forecasting and planning.

Model features:

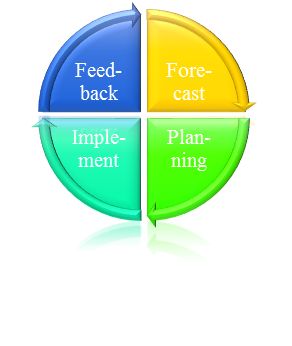
Time periodicity: model repeat along Forecast, Planning, Implementation, Feedback four stages in cycles, dynamically changing over time, as is shown in figure 1.

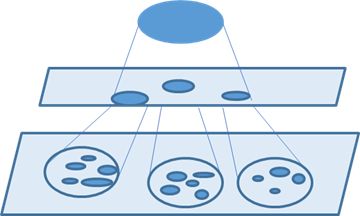
Space hierarchy: the overall geography is divided into regions, and regions are further divided into sub regions, forming a tree structure. The model considers the relationship between the integrity and localness and the relationship of localness itself, as is shown in figure 2.

Process integrity: the comprehensive consideration of medicine production, transportation, distribution makes the whole process to achieve the overall optimization in time consuming and money cost, as is shown in figure 3.

Figure 1 Time periodicity Figure 2 Space hierarchy

Figure 3 Process integrity

Ebola spread model based on SIQR: Aiming to establish a model about medicine eradicating the Ebola virus, this paper improved traditional SIQR model by adding the analysis of therapeutic effect of drugs and vaccines. The improved model can reflect the effect that the number of people who take vaccines and drugs has on Ebola outbreak. The model also takes integrity and localness relationships into account. Not only has the analysis of region internal contact transmission been studied, but also the contact transmission between regions. Through this model, we can predict the spread condition of Ebola under the different drug distribution (the number of people taking vaccines and drugs), further resulting in the optimization scheme.

Hierarchical medicine delivery system model: model divides the target geographical region and establishes a space hierarchical structure that considers a pharmaceutical factory as the initial medicine output node and each layer set its transfer station that can transfer drugs to other nodes and the transfer station is the medicine output node for next layer. In each layer, we calculate each nodes' weighted value of time and cost to medicine output node, then use the shortest path algorithm to calculate the weighted value of time and cost that each nodes spends transferring drugs to other nodes. The node that has the minimum sum of the two weighted values is the transfer station of the layer.

Medicine manufacturing optimization model: The pharmaceutical factory produces two kinds of medicine--vaccines and drugs. Medicine production rate is determined by the scale of a pharmaceutical factory, production funds and drug demand, and the scale of production depends on the investment of production equipment. This model divides the total investment of the pharmaceutical factory into two parts: production equipment investment and production funds. The total investment is influenced by the current epidemic situation. By balancing production ratio and the investment ratio of vaccine and drug, the model can obtain the medicine production rate when the spread of the Ebola is the minimum value.

1. Part1: The Spread of the Disease
   1. The establishment of the model

Spread of infectious diseases, in essence, is the result of direct or indirect contact among people of different spatial locations. Contact behavior among people is a very complex process. Studies generally assume that contacts among people are the behavior that is defined in the local area. However, with the progress of science and technology and social development, especially the invention of railways, aviation and other modern transport, which greatly enhances the ability of contact between people, the features of spatial contact between people increasingly exhibit global characteristics [3].

So in this model, we consider both the spread in one area and the spread between different areas. We assume that the people in one area are characterized to be in one of these states: susceptible (S), infected but not isolated (I), slightly infected and can be cured (), severely infected and can't be cured () and recovered or death (R). Then we consider the spread between different areas.

Considering the area is formed by k spatial regions, as ,stands for the total number of individual in spatial areas i [4].

For a region, we get the model as follows:

Figure 4 SIQR Model

From the above analysis, we get the expression:

stands for contact rate coefficient between region i and j. In this paper, we define based on fixed weight function that commonly used in geography study.

In geography study, for the bordering regions, we define the fixed weight function according to the ratio of the common boundary:

where

stands for the perimeter of the spatial region i;

stands for the perimeter of the spatial region j.

stands for the length of the shared border between areas i and j.

The above definition of the weight can express local contact behavior, but it does not describe the global contact behavior. As for global contact behavior, consider traffic conditions between two regions. The following is the definition of the fixed weight function based on traffic conditions between spatial region:

where

stands for the capacity of the highway;

stands for the capacity of the railway;

stands for the capacity of the aviation.

stands for the scaling factor of the highway;

stands for the scaling factor of the railway;

stands for the scaling factor of the aviation.

Finally, we define inter regional contact rate factor as follows [2]:

In the above formula,is in the condition that area i and area j have a common border area, but with no transit line connected them. is in the condition that there are transit lines connected area i and area j, but with no common border area between them., is in the condition that area i and area j have a common border area, and with transit lines connected them. is in the condition that there is no common border area or transit lines between area i and area.

1. Preliminary test of the model

In order to realize our model, we analyze the early data and fit the model to determine the parameters. Here, we first consider the situation where early measures such as isolation have not been taken. To fit the model we use 1stOpt software.

Next we collect 0-40 days of data of Guinea, and compare it with our model [5]. As the epidemic is just beginning, the appropriate measures, such as isolation and treatment, have not been taken. The following is the result we get:

Figure 5 The situation in Guinea in 0-40 days

As the figure shows, the data fits well. So we can come to the conclusion that our model is right.

Next, in the case of only isolated, we further predict the situation in only one node, we analyze the particular case of the node during 0-300 days. The following is the result we get:

Figure 6 The situation in one node in 0-300 days

Finally, we further predict the situation between nodes. We select six countries as examples, and

 

get the following figure by data visualization tools ECharts [6].

Figure 7 The simulation of epidemic

From the figure above, we can see that the affected people in Guinea are the most. This may be due to its health and medical conditions are relatively backward or people's insufficient attention to it or some other reasons.

1. Part2: Speed of Manufacturing of the Vaccine or Drug
   1. The establishment of the model

Based on the development of the epidemic and restrictions of production conditions, we establish the model to work out the proper speed of manufacturing of the vaccine or drug. Assuming that the total investment of the pharmaceutical factory is I, including the fund of expanding the scale of the production and the consumption in the production process. Both parts of the investment are respectively used for vaccines and drugs. As shown below:

 

 

 

 

 

 

 

 

 

 

 

 

 

Figure 8 The model of the investment of the pharmaceutical

 

are the corresponding investment funds.

Taking constraints of actual situations into account, like the financial, human resources, we assume that vaccine and drug delivered once a week.

In our paper, total investment of each part is not greater than the total investment, so:

The more severe epidemic is, the more total investment the pharmaceutical factory invests, so:

The change of the maximum production rate is caused by the investment, so the maximum production rates of the vaccines and drugs are as follows:

The production rates with restrictions of the fund in the production process are as follows:

 

stands for the production rate of the vaccine per dollar;

stands for the production rate of the drug per dollar

According to the above analysis, we get the actual production rate:

stands for the time when pharmaceutical began producing vaccines;

stands for the time when pharmaceutical began producing drugs, and .

Then we get the supply of vaccines per week: , the supply of drugs per week: .

Substituting the above formula into the optimization equation

We get that

.

stands the weight of vaccines and stands the weight of drugs.

1. Preliminary test of the model

Because of the limitation of the data, the time and cost for medicine development are not easy to estimate, so we assume that at the beginning of the test, the medicine has been developed.

According to our model, we refer to a large number of relevant literature and researches [7], and combining the actual situation, finally determine the related parameters of the model are as follows:

In this case, firstly, we assume that the pharmaceutical only produce vaccines, but no drugs. The following results are obtained:

Figure 9 The simulation of only producing vaccines

Compare the figure 6 with the figure 3 before, we learn that after vaccination, the number of new infections is greatly reduced, and to a certain extent the death toll reduce too.

However, in reality, we could not have turned a deaf ear to those who have been infected, so we would produce vaccines and as well as drugs. So when vaccines and drugs are produced at the same time, we get:

 

Figure 10 The simulation of producing vaccines and drugs.

Compare the figure 7 with the figure 6 before, we learn that the number of new infections is larger than that of only produce vaccines, it's probably because the general resources is certain, when producing vaccines and drugs at the same time, the amount of vaccine production decreases, so that the number of infections increases. The death toll is smaller than that of only produce vaccines, probably because of the role of the drug.

In addition, the simulation is based on the first part of the initial state of the model in which the preparation is not sufficient. If medical conditions have been further improved, the epidemic would be controlled better and more quickly.

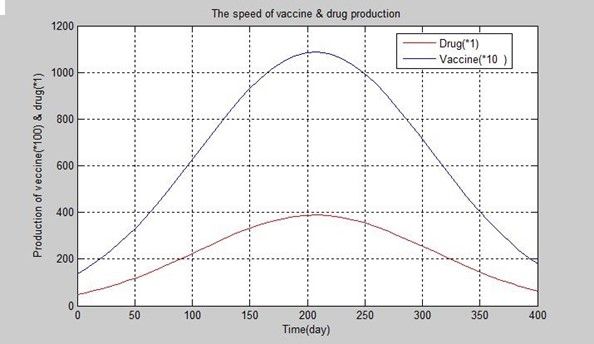
According to our model, we obtain the graph as follows by Matlab.

Figure 11 The speed of producing vaccines and drugs.

 

1. Part3: The Quantity of the Medicine Needed

In the paper, we consider the world medical association's new medication — the vaccine for immunization and the drug used to treat patients whose disease are not advanced.

The model assumes that the amount of vaccines a person takes is fixed, so is the amount of drugs a person. Therefore the amount of vaccines needed each week is , the amount of drugs needed each week is

And from the definition,

.

Then we simulate the model. Based on the model above, we select Sierra Leone of West Africa to simulate. We collect information from various channels combined with the actual situation, and choose thus we get results as follows:

Figure 12 The Quantity of the Medicine Needed

1. Part4: Delivery Systems

In this paper, we establish hierarchical transport systems, first we divide the epidemic area into various regions (eg nation), each region as a node in the network, select the transfer stations in the network, medicine are shipped from the factory to transfer stations and next transported to other sites. Then divide each region into several sub-regions(for example, dividing nations into provinces), and taking the transfer station as the drug output point of sub-regions, and the like. So a hierarchical transport system is formed. In order to work out the transfer system, we adopt the shortest path algorithm. And the selection of the transfer station should make optimal transportation time and costs. That's locations of delivery.

1. The establishment of the model

Firstly, we use a weighting factor P to weight the important of time efficiency and cost efficiency. The cost is calculated as:

where

is the efficiency of the transit time;

is the efficiency of the transit costs.

 

Where

T stands for the actual time that the transportation costs;

stands for the minimum time that the transportation costs;

stands for the maximum time that the transportation costs;

stands for the actual costs that the transportation spends;

stands for the minimum costs that the transportation spends;

stands for the maximum costs that the transportation spends.

In addition, according to the actual traffic conditions, the time and cost of transiting from pharmaceutical factory f to node i are as follows:

Table 1 The situation for pharmaceutical f to node i

Traffic mode	Time	Costs
		Vaccines	Medicine
Aviation
Railway
Highway
Marine transportation

 

Then we can get:

Substituting the above formula into the optimization equation

We can find the optimal transportation time and costs.

In the same, as for the situation between node i and node j, the time and cost of transiting between node i and node j are as follows:

Table 2 The situation for node i to node j

Traffic mode	Time	Costs
		Vaccines	Medicine
Aviation
Railway
Highway
Marine transportation

All the data above are based on the average of the maximum and minimum actual values when calculating.

Then we can get:

Substituting the above formula into the optimization equation

We can find the optimal transportation time and costs

As for the node i, the total time of transport vaccines needed once

where

stands for the costs for conserving in the transportation process.

Substituting the above formula into the optimization equation

We get

From the discussion above, we can come to the conclusion that when is at its minimum, the corresponding node i is the transfer station R. Thus we can build the delivery system by shortest path algorithm. The following is the pseudo code of the algorithm:

 

for each node[i] in G do path=shortest-path-algorithm(root,node[i]) //e.g. dijkstra algorithm for each edge[i] in path do mark edge[i] in G end end

 

1. The simulation of the model

Based on the model above, we simulate a delivery system of one layer as an example. We select Sierra Leone of West Africa to simulate. First of all, in order to determine the transport system parameters of the model, we collect information from various channels combined with the actual situation [8][9], and for each node, the distribution of vaccines and drugs is in accordance with the demand for transportation of the model, thus working out the edge weights between nodes.

And then to determine the position of the station with minimum weighted value, here we choose the weighted values between nodes are shown in the following figure. So we choose capital as the transfer station (because only the capital has an airport, so if not choosing the capital, the cost would apparently be larger).

Table 3 The costs between nodes

Musala	Kamakwie	Mudugu	Makeni	Kcardu	Kenerra
0.57	0.744	0.7	0.76	0.6	0.56
Pendembu	Kailahun	Ba	Saiama	Freetown (Capital)	--
0.74	0.74	0.64	0.77	0.13	--

In order to work out the transfer system, we adopt the shortest path algorithm. The result is as follows:

Figure 13 Transfer system

In figure 13, blue line stand for traffic lines between nodes, and yellow lines stand for traffic lines

used by transport system.

1. To Further Illustrate the Model

If

,

stands for the time difference that can be tolerated. Clustering regions in the system, and dividing these regions into multiple sub-systems. Each sub-system's transfer station is determined by the way above.

1. Supplementary Note

On the basis of sub-models above, our FPIF model repeat along the Forecast, Planning, Implementation, Feedback four stages in cycles, dynamically changing over time. To apply the model, first divide the target region into layers. Then, collect data about Ebola Historical Data, the current epidemic situation, traffic conditions, the current manufacturing capacity, capital investment and any other data needed. Based on these, we forecast the spread of the Ebola and determine the optimization scheme of manufacturing, delivery and distribution through Ebola spread model based on SIQR, hierarchical medicine delivery system model and medicine manufacturing optimization model. The optimization scheme helps arrange for manufacturing of the vaccine or drug in the next phase, implement the distribution plan and construct delivery systems. After the implementation of this phase, we report the feedback back to the model, and continue the forecasting and planning of the next phase. The feedback includes the latest epidemic situation, traffic conditions, the latest manufacturing capacity and other data the model needs.

Feedback process can be seen as a process of data collection and model parameter adjustment. Situations such as Ebola outbreak, vaccine and drug production are dynamic, requesting an ideal model to be adjusted with the changing circumstances. Therefore, the feedback link is included in as part of the model. Feedback data contains the latest information on the epidemic, transportation, funds and others needed, making parameter values of our model adjusted timely.

1. The General Simulation of the Model

First showing the situation of the overall simulation, here we still take six countries as examples, and according to the actual circumstances of the country to set the parameters of the model.

First, we collect the data of Ebola outbreak in western Africa in 2014, fitting the relevant data of the spreading of Ebola virus in our spreading model. We also read past studies for reference [10].Here we still use 1stOpt to calculate and use Runge-Kutta-Feh1berg Method algorithm to fit, in the fitting result, the value of Correlation is 0.999999998902. It fits well.

Primary experiment parameters are as follows:

Simulating our model by Matlab, we get the epidemic changes of six countries as follows:

Figure 14-20 The overall simulation

The figure 14 shows the situation of the country where the epidemic originally broke;

The figure 15 and the figure 16 show the situation of countries just being infected and starting spreading ;

The figure 17, the figure 18 and the figure 19 show the situation of countries where the epidemic outbreak and spread

From the results of the experiment, we learn that in our model, the outbreak has been controlled effectively.

We can also learn that: the epidemic ends almost at the same time in three most serious countries; the mortality is still not particularly low, could this be the result of more money being used in prevention; as shown in figures, the development of the overall outbreak is not exponential curve, there would be a period of acceleration after the international spread.

1. Future Improvements
   1. The Investment of Health Organizations

In the model, we can also consider the investment of health organizations. Some of the investment is used for the building of basic sanitation facilities, others is used to establish more pharmaceutical factory. As shown below:

Figure 14 The model of the investment of organizations

From the figure above, we learn that

After establishing more infrastructures, those infected people can be isolated more. So the number

 

of ratio about isolation is increased by the establishment of infrastructures. Then we get:

where

stands for the ratio of slightly infected people at present

stands for the ratio of severely infected people at present

stands for coefficient of investment as for

stands for coefficient of investment as for .

1. Transportation System of Multiple Pharmaceutical Factories

When considering more than one pharmaceutical factories, we can use the classic transportation model to establish the transportation system of multiple pharmaceutical factories. In this way, we can get the optimization scheme of transportation between the pharmaceutical factories.

1. The Production and Distribution of A Variety of Vaccines, Drugs

With the deepening of the research of epidemic diseases, human may be able to produce a variety of vaccines and drugs that can control the Ebola. So, in order to maximize the use of these vaccines and drugs, we need to consider the production and distribution of a variety of vaccines and drugs. We can use the production distribution model, in this way, to obtain the optimal production distribution mode, and to help more people.

1. Sensitivity Analysis

There might be some uncertainty in our parameters. This might influence the result of our model. To test the robustness of our model, we implement a sensitivity analysis. The analysis proves that our model does not demonstrate a chaotic behavior, showing a good sensitivity. We take stands for the average number of people contacted effectively per patient per week, determining the number of newly infected person. Reducing turnover and the contact with an infected person can decrease the value. We found that the number of infected people and the death increased as λ increased. The difference is more obvious over time, but the number of infected people and the death with differentobeys the same change trend. Therefore, plays an important role in the model.

Figure 21 Sensitivity analysis of

Next, we focus on another important variable .We analyze the development of the epidemic in the case of P taking 0.6, 0.7 and 0.8. Here the paper takes the global epidemic situation into consideration. No new cases within 21 days mean the end of the epidemic. When takes 0.6, we can see a larger number of cases, lower mortality, but the number of deaths is relatively high, and the duration of the epidemic is longer. Thus we can see that the increase of vaccine production is more efficient to control the outbreak.

Table 4 Sensitivity analysis of

	Cases	Deaths	Death Rate(%)	Duration(day)
0.6	2389	1572	0.658	120
0.7	1812	1247	0.6882	112
0.8	1678	1236	0.7366	110

Finally, we focus on another important variable .This factor is used to weigh the transfer cost and time.We also analyze the development of the epidemic in the case of P taking 0.6,0.7 and 0.8.We take the traffic situation in Sierra Leone for analysis. Capital is always the best choice. Actually, the capital has a convenient international airport landing, airdrop or other ways of transporting to other places would cost more waste generally.

Figure 22 Sensitivity analysis of

1. Conclusions

Based on our simulation of FPIF model, we can come to a conclusion that our FPIF model for controlling Ebola epidemic is very practical. From the analysis of the model we can learn that control and the eradication of Ebola, need to pay attention to many aspects, including:

As can be seen from the initial simulation of model part1, simply isolating cases of epidemic has little effect on controlling the epidemic, so we need more strict isolation and treatment to further control the condition, which is depended on the country's medical and health conditions.

Vaccines and drugs play a very important role in controlling the epidemic. Vaccines can control the spread of the epidemic effectively; medicines can reduce the mortality of epidemic. But as we can see, we face the shortage of drugs and vaccines against Ebola outbreak. Full preparation at any time will do no harm. So, establishing epidemic emergency funds and the system will help a lot.

A complete emergency response system can make the dealing of the epidemic in order, and save cost at the same time, which can make the financial and human resources flow to where it is needed urgently. Our optimized transport system is an excellent example.

 

1. Strengths and Weaknesses
   1. Strengths

• Our model is dynamic, and the target area is divided hierarchically.
• The model considers the relationship between the integrity and localness and the relationship of localness comprehensively
• We consider the various links such as production, transportation and distribution comprehensively.
• We successfully quantify various indicators and get the expected results by reasonable mathematical derivation.

1. Weaknesses

• The data is limited, and the accuracy of the data needs to be improved.
• Some of the parameters are based on semi-educated guess because few data are available.
• We define several restrictions to simplify calculation process.
• In our model, we make the number of deaths and rehabilitation with no treatment as one parameter.
• It is pretty tedious to calculate.

 

A letter for the world medical association

 

Dear all,

The outbreak of EVD in Western Africa has been proven to be far more difficult to control than previous epidemics and is now present in Sierra Leone, Liberia and Guinea with more than 4000 deaths. Theoretically, the mortality of EVD varies from 50% to 90%, while in reality the death rate of EVD is approximately 55%.

Fortunately, today we would like to tell you that we have successfully developed a medication that could stop Ebola and cure patients whose disease is not advanced. Besides, we also took into account some countries' current consolidation, and studied the propagation mechanism of Ebola, the quantity of the medicine needed, possible feasible delivery systems, locations of delivery, and the speed of manufacturing of the vaccine or drug. Our research can contribute to the gradual control and even the final eradication of Ebola. We desire to do everything we can to help those countries and people who suffer a lot.

We call on national and local governments to increase public communication about basic infection control practices. We also call on all nations to commit enhanced support for combatting the EVD epidemic.

Everyone who is or has been tortured by Ebola, should actively cooperate with the treatment. Medication for Ebola has been developed and would be on trial soon. We believe rehabilitation is just around the corner! We also suggest that everyone should hold a positive attitude towards the prevention of Ebola. Don't head for crowded places as much as you can, and be extra careful about personal hygiene.

At the same time, we strongly appreciate those working in these exceptional circumstances and facing in treating patients and in seeking to control the epidemic.

In addition, we also hope that everyone will not give up, and will not be defeated by Ebola!

In a word, we believe that Ebola is absolutely not a nightmare, and we will defeat it in the end! Just believe that every day is full of hope and love!

Yours sincerely.

 

References

[1] World Health Organization page for Ebola. 2015.2.8. http://apps.who.int/ebola/en/

[2] Ebola virus disease From Wikipedia, the free encyclopedia 2015.2.8 http://en.wikipedia.org/wiki/Ebola_virus_disease

[3] ZHONG Shao- bo, ZHANG Mao- lei, ZHENG Jin- yong et al. Simulation of spread of infectious diseases based on geo-entity. Computer Engineering and Applications， 2008， 44 (18): 190- 193.

[4] ZHONG Shao- bo, ZHANG Mao- lei, ZHENG Jin- yong et al. Complex spatial contact pattern simulation of the spread of infectious diseases. J Tsinghua Univ ( Sci & Tech), 2009, Vol. 49, No. 2.

[5] Ebola data and statistics From WHO 2015.2.8.

http://apps.who.int/gho/data/node.ebola-sitrep.quick-downloads?lang=en

[6] Echarts-Home 2015.2.9.

http://echarts.baidu.com/

[7] The professional online trade platform of the pharmaceutical industry. 2015.2.9.

http://www.cphi.cn/news/show-119813.html

[8] Google map 2015.2.9. https://www.google.com/maps/@10.2045559,-11.5209491,7z

[9] Traffic of The Republic of Sierra Leone 2015.2.9.

http://sierra-leone.33map.net/sierra-leone_02.php

[10] G. Chowella,d,*, N.W. Hengartnerb, C. Castillo-Chaveza,d, P.W. Fenimorea, J.M. Hymanc,The basic reproductive number of Ebola and the effects of public health measures: the cases of Congo and Uganda , Journal of Theoretical Biology 229 (2004) 119–126