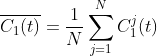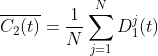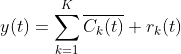CEEMDAN算法及其应用

目录

前言

一、CEEMDAN 算法

1 算法原理

2 MATLAB程序

二、CEEMDAN 算法的应用 

1 CEEMDAN—小波阈值联合去噪

2 CEEMDAN—小波包分析降噪

3 CEEMDAN—时频峰值滤波

结束语

参考文献

---

前言

针对EMD算法分解信号存在模态混叠的问题，EEMD和CEEMD分解算法通过在待分解信号中加入成对正负高斯白噪声来减轻EMD分解的模态混叠。但是这两种算法分解信号得到的本征模态分量中总会残留一定的白噪声，影响后续信号的分析和处理。

为了解决这些问题，TORRES 等提出了一种改进算法——完全自适应噪声集合经验模态分解（Complete EEMD with Adaptive Noise，CEEMDAN），又称完全集合经验模态分解。

CEEMDAN 分解从两个方面解决了上述问题：1）加入经 EMD 分解后含辅助噪声的 IMF 分量，而不是将高斯白噪声信号直接添加在原始信号中；2） EEMD 分解和 CEEMD 分解是将经验模态分解后得到的模态分量进行总体平均，CEEMDAN 分解则在得到的第一阶 IMF分量后就进行总体平均计算，得到最终的第一阶 IMF分量，然后对残余部分重复进行如上操作，这样便有效地解决了白噪声从高频到低频的转移传递问题。

一、CEEMDAN 算法

1 算法原理

设为经过 EMD 分解后得到的第 个本征模态分量，CEEMDAN 分解得到的第  个本征模态分量为，为满足标准正态分布的高斯白噪声信号，为加入白噪声的次数，为白噪声的标准表，为待分解信号。CEEMDAN 分解步骤如下：

1）将高斯白噪声加入到待分解信号得到新信号，其中q=1,2. 对新信号进行EMD分解，得到第一阶本征模态分量。

2）对产生的 N 个模态分量进行总体平均就得到CEEMDAN 分解的第 1个本征模态分量：

3）计算去除第一个模态分量后的残差：

4）在 中加入正负成对高斯白噪声得到新信号，以新信号为载体进行 EMD 分解，得到第一阶模态分量，由此可以得到 CEEMDAN 分解的第 2个本征模态分量：

5）计算去除第二个模态分量后的残差：

6）重复上述步骤，直到获得的残差信号为单调函数，不能继续分解，算法结束。此时得到的本征模态分量数量为 K，则原始信号被分解为：

2 MATLAB程序

clc;
clear;
close all;

fs=4000;   % 采样频率为4000Hz
t=(0:1/fs:(2-1/fs))';
N=length(t);
x1=0.25*cos(0.875*pi*50*t);
x2=0.3*sin(2*pi*50*t).*(1+1.5*sin(0.5*pi*40*t));
x3=0.15*exp(-15*t).*sin(200*pi*t);
x=x1+x2+x3;
nt=0.2*randn(N,1);
y=x+nt;

%% CEEMDAN分解
Nstd = 0.2;                % 高斯白噪声标准差，一般选择0-1
NR = 100;                  % 加入噪声的次数，一般选择50-100
MaxIter = 500;            % 最大迭代次数
[imf, its]=ceemdan(y,Nstd,NR,MaxIter);
[m, n]=size(imf);
CC=zeros(1,m);  % 相关系数
figure;
for i=1:m
    subplot(m/2,2,i);plot(imf(i,:));ylabel(['IMF',num2str(i)]);
    CC(i)=corr(imf(i,:)',y,'type','Pearson');   % 相关系数
end

CEEMDAN分解的各个IMF分量

CEEMDAN分解的各个IMF分量与待分解信号y(t)的相关系数

IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7
0.3702	0.2354	0.2431	0.2012	0.1793	0.7528	0.7492
IMF8	IMF9	IMF10	IMF11	IMF12	IMF13	IMF14
0.4566	0.0687	0.0287	0.0174	-0.0029	0.0111	0.0028

二、CEEMDAN 算法的应用 

利用CEEMDAN算法分解含噪声信号时，若将含噪声较多的 IMF分量直接舍弃，容易造成有效信息的缺失，因此，需要采用其他去噪方法对含噪声较多的高频 IMF分量进行去噪处理，最后将去噪后的 IMF分量和未去噪处理的 IMF分量进行重构，从而得到去噪后的信号。

1 CEEMDAN—小波阈值联合去噪

论文复现：CEEMDAN-小波阈值联合的球磨机筒体振动信号去噪方法研究。

首先运用 CEEMDAN 算法将信号分解成一系列 IMF 分量; 其次采用连续均方误差准则确定含噪声较多的高频 IMF 分量; 然后采用小波阈值去噪方法对含噪声较多的高频 IMF 分量进行去噪处理; 最后将去噪处理的 IMF 分量和未去噪处理的 IMF 分量进行重构，获得联合去噪方法去噪后的信号。

MATLAB代码链接：CEEMDAN—小波阈值联合去噪

2 CEEMDAN—小波包分析降噪

论文复现：基于 CEEMDAN -小波包分析的隧道爆破信号去噪方法。

首先，通过 CEEMDAN 分解得到多个本征模态分量，利用相关系数筛选出包含噪声的模态分量，并通过模态分量的频谱图及方差贡献率进行校核。然后，利用小波包阈值降噪方法对含有噪声的模态分量进行处理。最后，将未经处理的模态分量与去噪完成的模态分量进行重构，得到最终纯净的爆破振动信号。同时，通过小波包能量谱分析验证此降噪方法的可行性。

MATLAB代码链接：CEEMDAN—小波包分析降噪

3 CEEMDAN—时频峰值滤波

论文复现：基于 CEEMDAN 的时频峰值滤波微地震随机噪声压制方法。

原始微地震数据经 CEEMDAN 分解为若干个本征模态分量 IMF；通过计算 IMF 的样本熵将 IMF 划分为需滤波和存留的两个组分，对需 TFPF 滤波的 IMF 分量逐一选择时窗长度进行滤波；将处理后的 IMF 与不需处理的 IMF 重构即可得到最终的滤波信号。

MATLAB代码链接：

结束语

大家的点赞和关注是博主最大的动力，博主所有博文中的代码文件都可分享给您（除了少量付费资源），如果您想要获取博文中的完整代码文件，可通过C币或积分下载，没有C币或积分的朋友可在关注、点赞和评论博文后，私信发送您的邮箱，我会在第一时间发送给您。博主后面会有更多的分享，敬请关注哦！

参考文献

[1] TORRES M E, COLOMINAS M A, SCHLOTTHAUER G, et al. A complete ensemble empirical mode decomposition with adaptive noise[C] // IEEE International Conference on Acoustics, Speech and Signal Processing, IEEE, 2011 :4144-4147.

[2] 蔡改贫, 赵小涛, 胡显能, 等. CEEMDAN-小波阈值联合的球磨机筒体振动信号去噪方法研究[J]. 机械科学与技术, 2020, 39(7) : 1077-1085.

[3] 王海龙，赵岩，王海军，彭婵媛，仝潇．基于 CEEMDAN -小波包分析的隧道爆破信号去噪方法．爆炸与冲击.（网络首发）

[4] 陈毅军，程 浩，巩恩普，等. 基于 CEEMDAN 的时频峰值滤波微地震随机噪声压制方法[J]. 石油地球物理勘探，2021,56(2)：234-241.