自适应滤波器（一）LMS自适应滤波器

1. 自适应滤波器简介

  在很多信号处理系统中，并没有信号的先验统计特性，不能使用某一固定参数的滤波器来处理，比如信道均衡、回声消除以及其他因素之间的系统模型等，均采用了调整系数的滤波器，称为自适应滤波器。这样的滤波器结合了允许滤波器系数适应于信号统计特性的算法。

• 自适应滤波器的特点
  • 没有关于待提取信息的先验统计知识
  • 直接利用观测数据依据某种判据在观测过程中不断递归更新
  • 最优化
• 自适应滤波器分类
  • 按结构分：横向结构、格型结构
  • 按算法分：随机梯度、最小二乘
  • 按处理方式分：成批处理、递归处理
• 自适应滤波器应用
  • 噪声抵消
  • 回音消除
  • 谱线增强
  • 通道均衡
  • 系统辨识

2. 自适应滤波器原理

2.1 原理概述

  自适应滤波器的原理框图如下图所示，输入信号x(n) 通过参数可调数字滤波器后产生输出信号 y(n)，将其与***期望信号d(n)*进行比较，形成误差信号e(n)， 通过自适应算法对滤波器参数进行调整，最终使 *e(n)*的均方值最小。自适应滤波可以利用前一时刻已得的滤波器参数的结果，自动调节当前时刻的滤波器参数，以适应信号和噪声未知的或随时间变化的统计特性，从而实现最优滤波。自适应滤波器实质上就是一种能调节自身传输特性以达到最优的维纳滤波器。自适应滤波器不需要关于输入信号的先验知识，计算量小，特别适用于实时处理。维纳滤波器参数是固定的，适合于平稳随机信号。卡尔曼滤波器参数是时变的，适合于非平稳随机信号。然而，只有在信号和噪声的统计特性先验已知的情况下，这两种滤波技术才能获得最优滤波。在实际应用中，常常无法得到信号和噪声统计特性的先验知识。在这种情况下，自适应滤波技术能够获得极佳的滤波性能，因而具有很好的应用价值。

2.2 模型分析

  自适应滤波器的详细模型如下图所示。

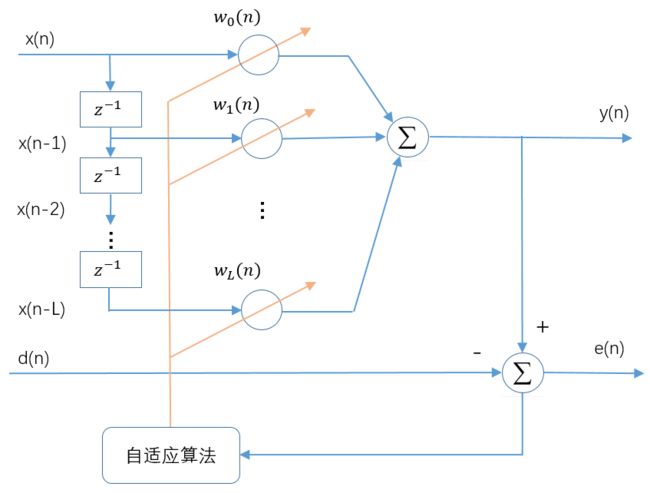
输入信号矢量：
$$\mathbf{x}(n)=[x(n)x(n-1)\dots x(n-L){]}^T$$
输出$y(n)$为：
$$y(n)=\sum _{k=0}^L{w}_k(n)x(n-k)$$
自适应线性组合器的L+1个权系数构成一个权系数矢量，称为权矢量，用$w(n)$表示，即
$$\mathbf{w}(n)={\left[w_0(n)w_1(n)\dots w_L(n)\right]}^T$$
因此$y(n)$可以表示为：
$$y(n)=x^T(n)\mathbf{w}(n)={\mathbf{w}}^T(n)\mathbf{x}(n)$$
误差信号为：
$$e(n)=d(n)-y(n)=d(n)-x^T(n)w(n)=d(n)-{\mathbf{w}}^T(n)\mathbf{x}(n)$$
自适应线性组合器按照误差信号均方值最小的准则，即：
$$\xi (n)=E\left[e^2(n)\right]=E\left[d^2(n)\right]+{\mathbf{w}}^T(n)E\left[\mathbf{x}(n){\mathbf{x}}^T(n)\right]\mathbf{w}(n)-2E\left[d(n){\mathbf{x}}^T(n)\right]\mathbf{w}(n)$$
输入信号的自相关矩阵为：

期望信号与输入信号的互相关矩阵为：

则均方误差的简单表示形式为：
$$\xi (n)=E\left[d^2(n)\right]+{\mathbf{w}}^{T}R\mathbf{w}-2P^T\mathbf{w}$$
从该式可看出，在输入信号和参考响应都是平稳随机信号的前提下，均方误差是权矢量的各分量的二次函数。该函数图形是L+2维空间中一个中间下凹的超抛物面，有唯一的最低点,该曲面称为均方误差性能曲面，简称性能曲面。

均方误差性能曲面的梯度：
$$\nabla =\frac{\partial \xi }{\partial w}=2\mathbf{R}\mathbf{w}-2\mathbf{P}$$
令梯度 $\nabla$ 等于零，可求得最小均方误差对应的最佳权矢量或维纳解 ${\mathbf{W}}^{\ast }$，解得 ${\mathbf{w}}^{\ast }={\mathbf{R}}^{-1}\mathbf{P}$。

虽然维纳解的表达式我们知道了，但仍然有几个问题：

1. 需要知道$R$和$P$，而这两个都是我们事先不知道的
2. 矩阵的逆需要的计算量太大：$O(n^3)$
3. 如果信号是非平稳的，$R$和$P$每次都不一样，需要重复计算

2.3 梯度下降法

  一般情况下，我们使用递归的方法来寻找多变量函数的最小值，其性能指标就是MSE(Mean Square Error)，它是滤波器系数的二次函数，因此该函数具有唯一的最小值。一般是采用梯度下降的方法来进行迭代搜索出最小值，梯度下降又分为梯度下降、随机梯度下降和批量梯度下降。

  使用迭代搜索的方式一般都只能逼近维纳解，并不等同于维纳解。

  下面我们先来看梯度下降法，再来看下前面的公式：（梯度下降的原理可参考我的另一篇文章：梯度下降算法 线性回归拟合）

误差信号为：
$$e(n)=d(n)-y(n)=d(n)-x^T(n)w(n)=d(n)-{\mathbf{w}}^T(n)\mathbf{x}(n)$$
均方误差为：
$$J=E\left[e^2(n)\right]=E\left[d^2(n)\right]+{\mathbf{w}}^T(n)E\left[\mathbf{x}(n){\mathbf{x}}^T(n)\right]\mathbf{w}(n)-2E\left[d(n){\mathbf{x}}^T(n)\right]\mathbf{w}(n)$$
利用最陡下降算法，沿着性能曲面最速下降方向（负梯度方向）调整滤波器强权向量，搜索性能曲面的最小点，计算权向量的迭代公式为：
$$\mathbf{w}(n+1)=\mathbf{w}(n)+\mu (-\nabla \mathbf{J})$$
其中$u$为步长因子，$u$的取值需要满足下式，其中${\lambda }_{max}$表示输入信号自相关矩阵的最大特征值。
$$\left|1-2\mu {\lambda }_{\max }\right|<1\Rightarrow 0<\mu <\frac{1}{{\lambda }_{\max }}$$
由于计算特征值比较复杂，有时为了避免计算特征值，可采用计算矩阵迹的方法，因为自相关矩阵$\mathbf{R}$是正定的，因此有：
$$t_r[\mathbf{R}]=\sum _{k=0}^L{\lambda }_k>{\lambda }_{\max }$$
这里，$t_r[\mathbf{R}]$是$\mathbf{R}$的迹，它可以用输入信号的取样值进行估计，即：
$$t_r[\mathbf{R}]=\sum _{k=0}^{L}E\left[x_i^2(n)\right]$$
因此有：
$$0<\mu <t_r^{-1}[\mathbf{R}]$$

在梯度下降算法中，为获得系统的最佳维纳解，需要知道输入信号和期望信号的相关信息，当期望信号未知时，就无法确定它们的相关特性，必须对梯度向量进行估计。

LMS自适应算法直接利用瞬态均方误差对瞬时抽头向量（滤波器系数）求梯度：
$$\hat{\nabla }\mathbf{J}=\frac{\partial \left(e^2(n)\right)}{\partial w(n)}={\left[2e(n)\frac{\partial e(n)}{\partial w_1(n)},2e(n)\frac{\partial e(n)}{\partial w_2(n)},\cdots ,2e(n)\frac{\partial e(n)}{\partial w_M(n)}\right]}^T=-2e(n)\mathbf{x}(n)$$
由此可得传统LMS自适应滤波算法流程如下：
KaTeX parse error: Unknown column alignment: y at position 16: \begin{array} y̲y(n)=\boldsymbo…

下面我们来看一个实际的仿真：

close all;clear all;clc;

%% 产生测试信号
fs = 1;
f0 = 0.02;
n = 1000;
t = (0:n-1)'/fs;
xs = cos(2*pi*f0*t);
ws = awgn(xs, 30, 'measured');

% figure;
% subplot(211);plot(t, xs);title('原始信号');
% subplot(212);plot(t, ws);title('加噪信号');

M  = 20 ;   % 滤波器的阶数
xn = ws;
dn = xs;
% rho_max = max(eig(ws*ws.'));   % 输入信号相关矩阵的最大特征值
% mu = (1/rho_max) ;    % 收敛因子 0 < mu < 1/rho
mu = 0.001;
[yn,W,en] = lmsFunc(xn,dn,M,mu);

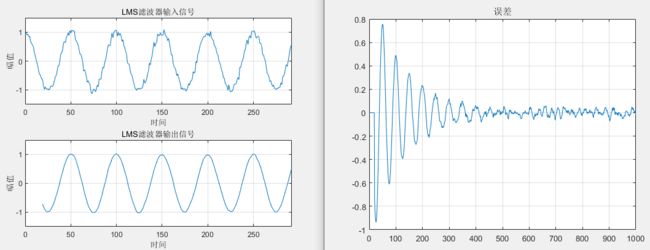
figure;
ax1 = subplot(211);
plot(t,ws);grid on;ylabel('幅值');xlabel('时间');
ylim([-1.5 1.5]);title('LMS滤波器输入信号');

ax2 = subplot(212);
plot(t,yn);grid on;ylabel('幅值');xlabel('时间');title('LMS滤波器输出信号');
ylim([-1.5 1.5]);linkaxes([ax1, ax2],'xy');

figure;plot(en);grid on;title('误差');

其中LMS滤波器函数如下：

% 输入参数:
%   xn   输入的信号
%   dn   所期望的响应
%   M    滤波器的阶数
%   mu   收敛因子(步长)
% 输出参数:
%   W    滤波器系数矩阵  
%   en   误差序列 
%   yn   滤波器输出        
function [yn, W, en]=lmsFunc(xn, dn, M, mu)
itr = length(xn);
en = zeros(itr,1);            
W  = zeros(M,itr);    % 每一列代表-次迭代,初始为0
% 迭代计算
for k = M:itr                  % 第k次迭代
    x = xn(k:-1:k-M+1);        % 滤波器M个抽头的输入
    y = W(:,k-1).' * x;        % 滤波器的输出
    en(k) = dn(k) - y ;        % 第k次迭代的误差
    % 滤波器权值计算的迭代式
    W(:,k) = W(:,k-1) + 2*mu*en(k)*x;
end

yn = inf * ones(size(xn)); % 初值为无穷大是绘图使用，无穷大处不会绘图
for k = M:length(xn)
    x = xn(k:-1:k-M+1);
    yn(k) = W(:,end).'* x;  % 最终输出结果
end

这里可能有同学对期望信号会有疑惑，期望信号都是已知的了，还滤波干嘛？LMS滤波器还有什么用？

1. LMS滤波器的应用场景比较多，比如在机器学习中，期望确实是已知的，我们希望通过迭代训练出合适的滤波器系数；
2. 在语音信号的线性预测中，将延时后的输入信号作为参考信号$d(n)$，即$d(n)=x(n-i)$；
3. 在自适应回音消除中，期望信号的输入就是回声通道产生的回声。

LMS算法的优缺点：

• 优点：算法简单，易于实现，算法复杂度低，能够抑制旁瓣效应
• 缺点
  • 收敛速率较慢，因为LMS滤波器系数更新是逐点的（每来一个新的$x(n)$和$d(n)$，滤波器系数就更新一次）,每一次采样点梯度的估计对于真实梯度会存在误差，导致滤波器系数的每次更新不会严格按照真实梯度方向更新，而是有一定的偏差
  • 跟踪性能较差，并且随着滤波器阶数(步长参数)升高，系统的稳定性下降
  • LMS要求不同时刻的输入向量$x(n)$线性无关——LMS 的独立性假设。如果输入信号存在相关性，会导致前一次迭代产生的梯度噪声传播到下一次迭代，造成误差的反复传播，收敛速度变慢，跟踪性能变差。

  正是由于LMS算法的缺陷，后面才有了NLMS、RLS等算法，我们会在后面的文章中一一讲到。

附：上述仿真的Python代码如下：

# This is a sample Python script.

# Press Shift+F10 to execute it or replace it with your code.
# Press Double Shift to search everywhere for classes, files, tool windows, actions, and settings.

import numpy as np
import matplotlib.pyplot as plt
import scipy.io as scio


# 信号加噪
def awgn(x, snr):
    snr = 10 ** (snr / 10.0)
    xpower = np.sum(np.abs(x) ** 2) / len(x)
    npower = xpower / snr
    if type(x[0]) != np.complex128:
        return x + np.random.randn(len(x)) * np.sqrt(npower)
    else:
        return x + np.random.randn(len(x)) * np.sqrt(npower / 2) + 1j * np.random.randn(len(x)) * np.sqrt(npower / 2)


def lmsFunc(xn, dn, M, mu):
    itr = len(xn)
    en = np.zeros((itr, 1))
    W = np.zeros((M, itr))
    for k in range(M, itr):
        if k==20:
            x = xn[k-1::-1]
        else:
            x = xn[k-1:k-M-1:-1]
        try:
            y = np.dot(W[:, k - 2], x)
            print(y)
        except:
            pass
        en[k-1] = dn[k-1] - y
        W[:, k-1] = W[:, k - 2] + 2 * mu * en[k-1] * x

    yn = np.ones(xn.shape) * np.nan
    for k in range(M, len(xn) ):
        if k == 20:
            x = xn[k - 1::-1]
        else:
            x = xn[k - 1:k - M - 1:-1]
        yn[k] = np.dot(W[:, -2], x)

    return yn, W, en


if __name__ == '__main__':
    fs = 1
    f0 = 0.02
    n = 1000
    t = np.arange(n)/fs
    xs = np.cos(2*np.pi*f0*t)
    ws = awgn(xs, 20)
    # data1 = scio.loadmat('xs.mat')
    # data2 = scio.loadmat('ws.mat')
    # xs = data1['xs'].flatten()
    # ws = data2['ws'].flatten()

    M = 20
    xn = ws
    dn = xs
    mu = 0.001
    yn, W, en = lmsFunc(xn, dn, M, mu)

    plt.figure()
    plt.subplot(211)
    plt.plot(t, ws)
    plt.subplot(212)
    plt.plot(t, yn)

    plt.figure()
    plt.plot(en)
    plt.show()

欢迎关注微信公众号：Quant_Times

欢迎大家学习我的课程：
System Generator & HLS数字信号处理教程