论文分享-- >异常检测-- >Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection
博客内容将首发在微信公众号"跟我一起读论文啦啦",上面会定期分享机器学习、深度学习、数据挖掘、自然语言处理等高质量论文,欢迎关注!

本文将总结分享ICLR2018论文 Deep Autoencoding Gaussian Mixture Model for Unsupervised Anomaly Detection,论文链接 DAGMM,参考的代码链接 CODE,本论文旨在将神经网络、EM与GMM有机结合起来,做无监督的异常检测,并且取得了不错的效果。
论文动机和创新点
-
异常检测的本质是通过密度估计找出异常样本过程。
-
如何对高维和多变量的数据进行无监督异常检测是一个挑战,传统的聚类算法,例如K-means,GMM,很难很好的应用到这类高维数据上。
-
对高维数据进行异常检测,传统的方法分两步,先对高维数据进行降维,将原始数据映射到低维度空间;然后在这个低维空间内做密度估计。
① 这两个步是相互独立的过程,高维数据降维后的表征很难保留足够多的关键信息。
② 因为这两步是相互独立的,最终可能导致模型陷入局部最优的境地,试想降维过程完全独立于后面密度估计过程,并不知道为后面的密度估计过程保留哪些关键信息。 -
异常样本与正常样本通常在两个方面不同:
① 在低维空间上,正常样本与异常样本在关联特征上有明显的不同。
② 相对正常样本,异常样本很难去重构,这也是许多用自编码做异常检测的原因。
在目前已有的异常检测方法,都是利用上面两种不同中的一种去做异常检测,导致模型总是次优表现。 -
目前有许多用深度自编码做异常检测,但是自编码极有可能陷入局部最优,于是采用了预训练的方法,但大多实验表明,pretrain、finetune的方法对模型的提升并没有那么的大(本人做过类似实验验证过)。
-
本论文提出的DAGMM模型,很巧妙的将降维过程(Deep AutoEncoding,以下简称DAE)和密度估计过程(Gaussian mixture model,以下简称GMM)有机的结合在一起,进行端到端的联合训练。避免了因两步独立导致模型陷入局部最优的境地。
-
DAGMM模型有着强大的容量足以拟合高维复杂的数据,并且巧妙利用EM算法思想,(这种方式给人眼前一亮的感觉)来优化GMM模型,使得DAE与GMM可以联合训练,实验结果表明,DAGMM模型比state of art方法,在F1指标上提高了14个点,效果相当惊艳了。
网络结构
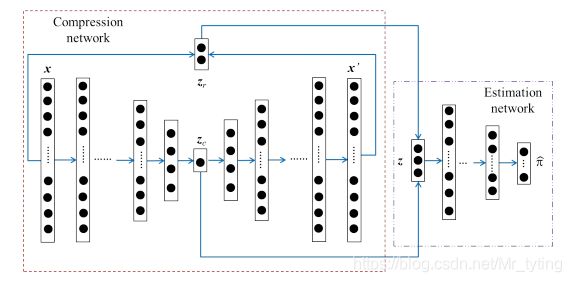
上图为DAGMM的整体网络结构,分两个子结构,左边部分为Compression network,是一个深度自编码网络,通过这个自编码我们可以得到输入x的低维表示 z c z_c zc,同时得到输入 x x x 与重构的 x ′ x' x′ 之间的重构误差特征 z r z_r zr, z r z_r zr 与 z c z_c zc 进行拼接操作形成 z z z;右边为 Estimation network,也是一个多层的神经网络,输入为 z z z, 经过多层全连接得到一个概率分布,这个概率分布的长度即为混合高斯分布中子分布个数。
Compression network
就是一个深度自编码网络,网络内具体结构,可以根据数据或业务做不同处理。
z c = h ( x ; θ e ) , x ′ = g ( z c ; θ d ) (1) z_c=h(x;\theta_e),\ x'=g(z_c;\theta_d) \tag1 zc=h(x;θe), x′=g(zc;θd)(1)
z r = f ( x , x ′ ) (2) z_r = f(x,x') \tag2 zr=f(x,x′)(2)
z = [ z c , z r ] (3) z=[z_c,z_r] \tag3 z=[zc,zr](3)
公式 2 计算的是重构误差,论文中采用的欧式距离、余弦相似度这两度量方式计算重构误差。具体为啥采用这两种误差度量方法,附录中有讲到,作者做实验时发现,在原始维度为20维的数据集上,大部分异常样本在低维空间(论文中讲20维降低到1维)上与正常样本有明显的分离,但是存在部分异常样本隐藏在正常样本内,同时这些异常样本在原始的20维空间内,与正常样本又有明显的不同。于是作者计算了所有样本的L2重构误差(欧式距离)。
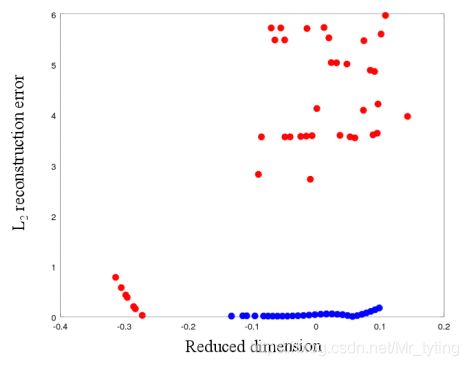
上图横坐标表示降低后的维度上(1维,自编码学习到的,每个样本原始20维),纵坐标表示这些样本L2重构误差。其中红点表示异常点,绿点表示正常样本,显然有明显的分离性。
论文中还讲到选择重构误差的度量方法,需要满足两个条件:
① 连续可导 ; ② 数值范围上应该相对较小。
Estimation network
估计网络是本文的关键,如何把神经网络与EM算法有机结合,做到DAE与GMM联合训练,相互优化是论文的一大亮点。
EM算法简介
要读懂这部分,必须得对EM算法有着深入的了解,EM算法用于含有隐变量(Hidden variable)的概率模型参数的最大似然估计。主要有以下两步:
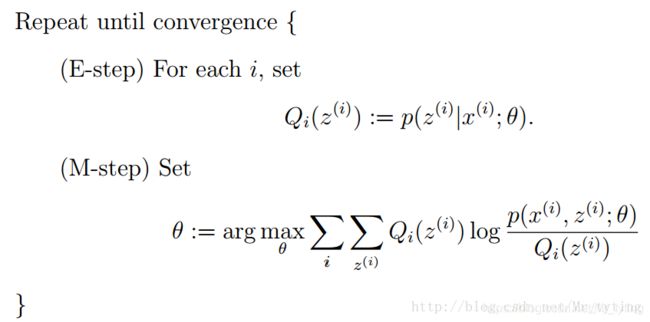
上式中x为观测值,Z为隐变量,Q为Z的分布。E步更新Q,使得下界函数与对数似然函数在θ点处相等;而M步是在求下界函数的极大值,并且更新θ。这两步不断的循环重复。最终使得M步下界函数的最大值与对数似然函数的局部极大值相等。E步与M步不断循环,迭代更新参数 θ \theta θ。详细请看 EM
个人认为EM算法的核心思想,就是已知一批观测样本x,并且不同观测样本服从不同的隐分布z,这个时候无监督的构造某个分布(参数为 θ \theta θ) 使得似然函数 p ( x , z ∣ θ ) p(x, z| \theta) p(x,z∣θ) 极大化,那么这个分布就能拟合观测样本的真实分布。
对于单高斯分布,我们直接可以利用极大似然来优化求解。而对于多高斯分布,我们不知道不同观测样本服从哪些子高斯分布,因此可以采用EM算法来优化GMM。具体如下:
每次迭代包含两个步骤:
E-step:初次迭代需随机初始化K个高斯分布,非初次可由M步得到各个分布。每个观测样本x都能
计算出其在各个分布中的值,然后做softmax,得到样本x属于各个分布的概率。
M-step:对下界函数求极大,计算新一轮迭代的模型参数。
那么高斯混合分布中的多个不同的子分布就是EM算法中的隐变量(有没有感觉EM与GMM很配)。详情可以看链接 高斯混合模型 。
由上面EM算法的简介,可知其中的E步,M步是相互迭代过程,整体上是独立学习过程,那么如何把他和神经网络结合起来呢?论文中使用的不是标准的EM算法,而是借鉴了其思想。
GMM训练与参数更新
在Estimation network中,会得到样本属于高斯混合分布中各个分布的概率 γ ^ \hat{\gamma} γ^ :
p = M L N ( z ; θ m ) , γ ^ = s o f t m a x ( p ) p = MLN(z; \theta_m),\hat{\gamma} = softmax(p) p=MLN(z;θm),γ^=softmax(p)
假设我们先验性的认为应该有K个不同子分布的高斯混合分布,那么 γ ^ \hat{\gamma} γ^ 就是k维的向量。这一步就相当于EM算法中的E步,这样就确定了样本属于各个隐空间概率。
下面我们将此代入M步中,求下界函数极值时的参数,也就是对参数求导,求下界函数导数为零时参数的值,可得以下:

上式中的, ϕ ^ k , μ ^ k , Σ ^ k \hat{\phi}_k, \hat{\mu}_k, \hat{\Sigma}_k ϕ^k,μ^k,Σ^k 分别表示第k个分布在GMM里的概率,均值,协方差。当取上面这些值时,下界函数可取极大值。(注意 ϕ ^ k , μ ^ k , Σ ^ k \hat{\phi}_k, \hat{\mu}_k, \hat{\Sigma}_k ϕ^k,μ^k,Σ^k取值结果是由Estimation network的输出p决定的,并不是模型学习的参数。)
得到这些 ϕ ^ k , μ ^ k , Σ ^ k \hat{\phi}_k, \hat{\mu}_k, \hat{\Sigma}_k ϕ^k,μ^k,Σ^k 取值后,我们直接将其带入到高斯混合分布公式中得:
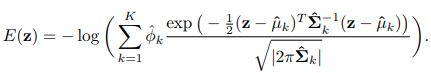
理论上这个似然函数越小(因为取负了),得出高斯混合模型越能拟合观测样本。
预测
当模型训练好后,来了一批预测样本,直接将计算这些预测样本的E(z) 值,值越大可能就越异常,可根据先验知识,设一阈值。
损失函数
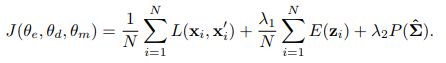
第一项:自编码的重构误差
第二项:高斯混合模型的似然函数(可以反向更新DAE参数,同时DAE又可更新GMM中的均值,协方差等)
第三项:防止矩阵不可逆
个人总结
- 论文中的Estimation network的输入不仅包含样本降维后表示,而且包含了重构误差特征,这一点比较特别也很重要。
- 该算法将EM算法的E步骤中的样本属于各子分布概率替换为端到端架构中子Estimation network的输出。并且由利用EM算法中的M步对GMM中的均值,协方差等做参数估计,然后极大化似然函数。这是该论文一大亮点。
- 该算法将降维过程和密度估计过程进行联合训练,相对传统的独立训练方式,更容易脱离局部最优。