【学习笔记】 matlab数字信号处理（四）信号的频域分析
第四章、信号的频域分析
4.1 概述
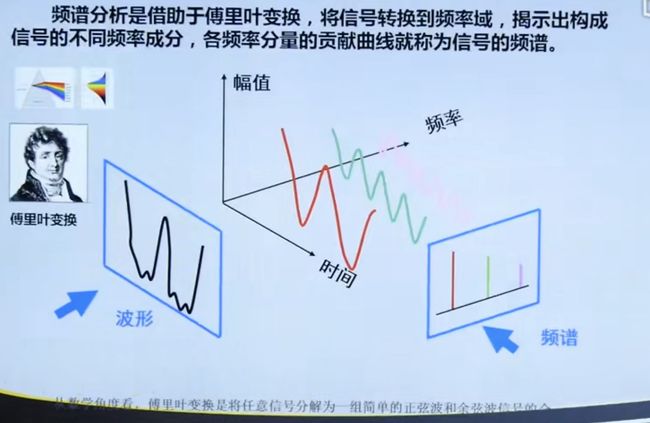
4.1.1 时域分析的局限性
4.1.2 频谱分析的优点
- 方便对复杂信号进行分析
- 抗干扰能力强
- 具有明确的物理意义
4.2 周期信号频谱分析
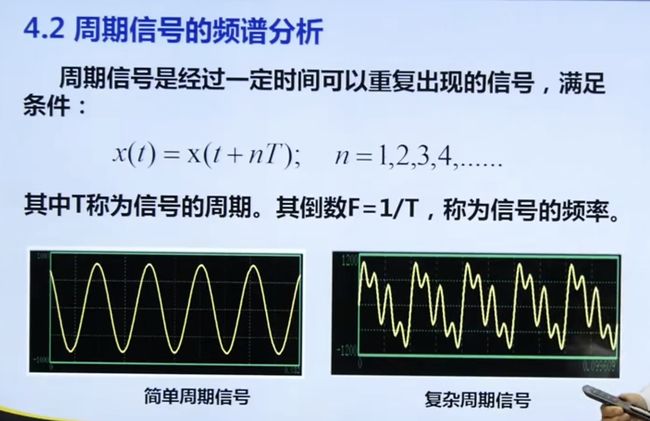
4.2.1 正交分解与合成
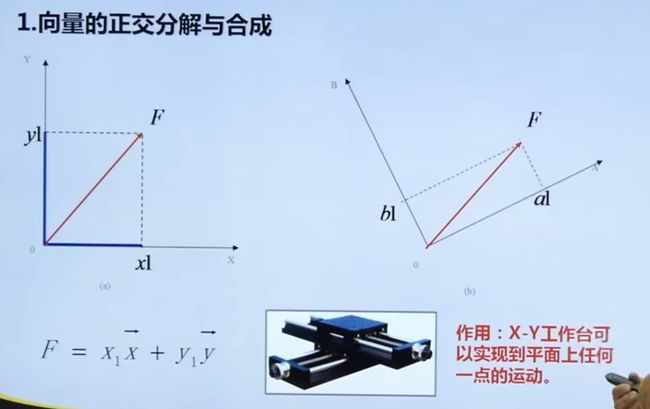
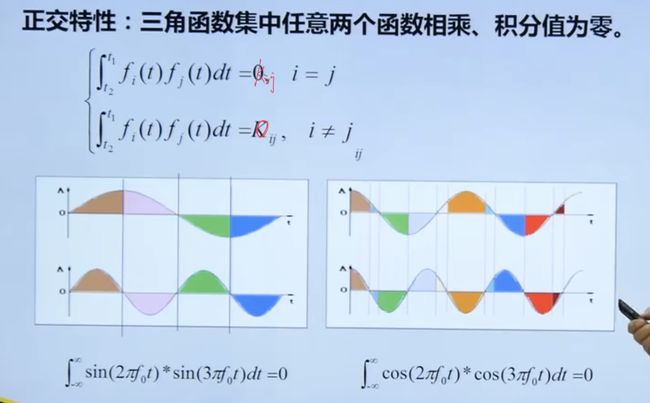
周期信号可以用三角成交函数表示
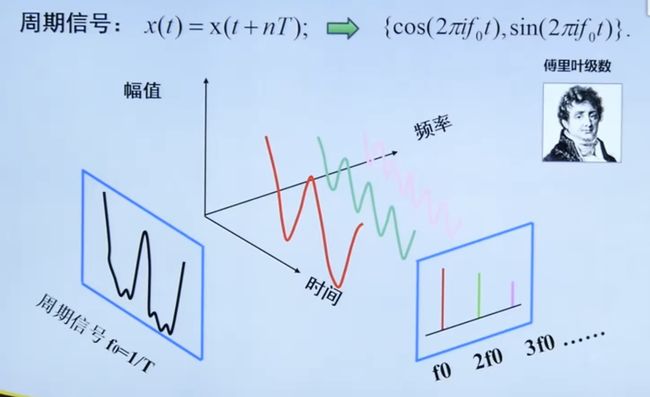
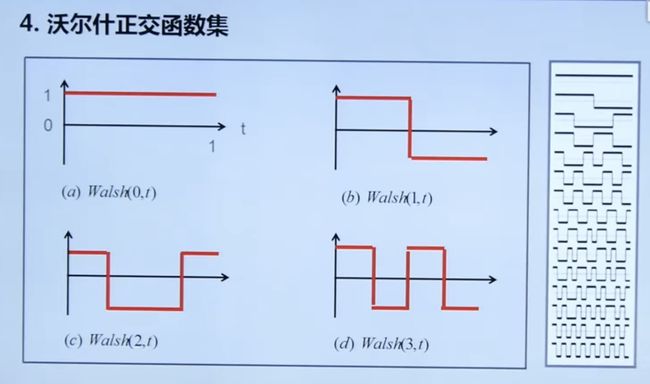
由于沃尔什正交函数集的频谱物理意义不明确，所以使用的较少。
4.2.2 周期信号的三角分解与合成
方波信号的分解与合成
MATLAB实现
% 方波信号的合成
N = 1024;T=2;
x = linspace(0,T,N);
y1 = sin(2*pi*x);
subplot(4,1,1)
plot(x,y1)
y2 = y1 + 1/3*sin(3*2*pi*x);
subplot(4,1,2)
plot(x,y2)
y3 = y2 + 1/5*sin(5*2*pi*x);
subplot(4,1,3)
plot(x,y3)
y4 = y3 + 1/7*sin(7*2*pi*x);
subplot(4,1,4)
plot(x,y4)
结果：
锯齿波的分解与合成
MATLAB实现
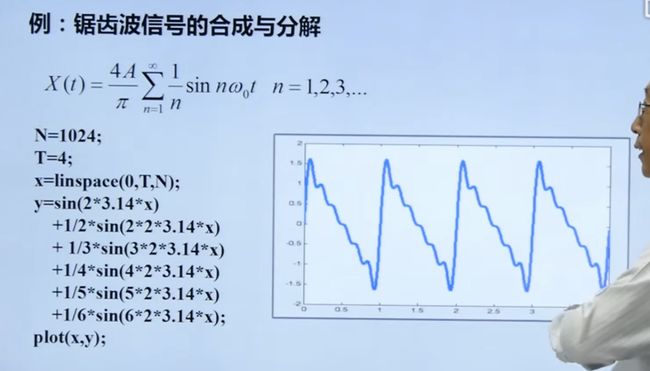
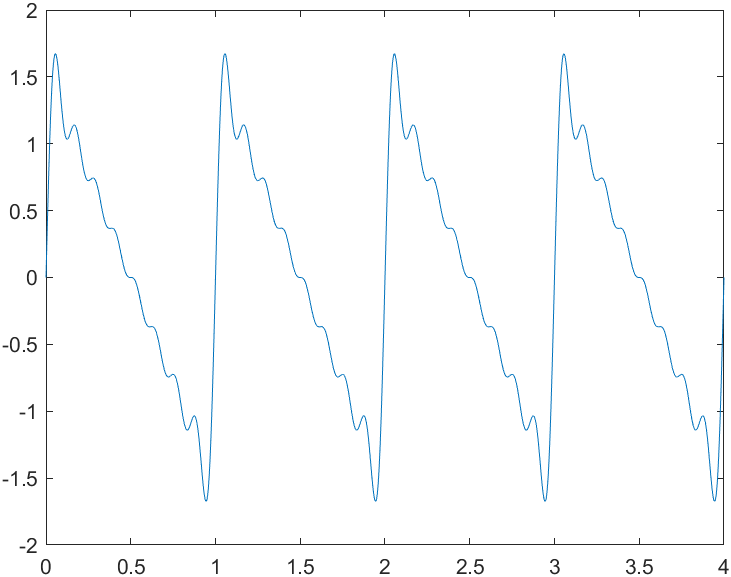
% 锯齿波信号的合成
N = 1024;T=4;
x = linspace(0,T,N);
y = sin(2*pi*x)...
+ 1/2*sin(2*2*pi*x)...
+ 1/3*sin(3*2*pi*x)...
+ 1/4*sin(4*2*pi*x)...
+ 1/5*sin(5*2*pi*x)...
+ 1/6*sin(6*2*pi*x)...
+ 1/7*sin(7*2*pi*x)...
+ 1/8*sin(8*2*pi*x);
figure
plot(x,y)
结果：
4.2.3 频谱图
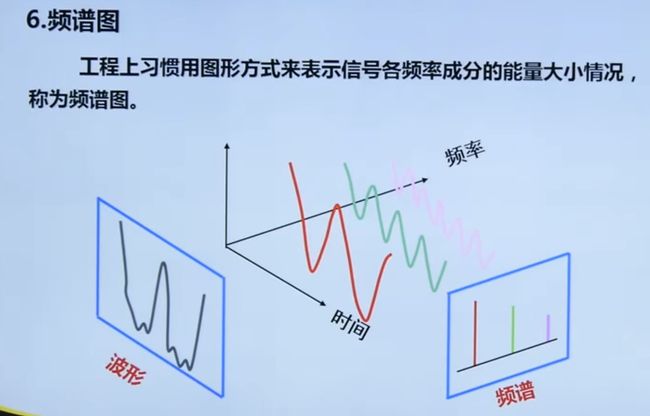
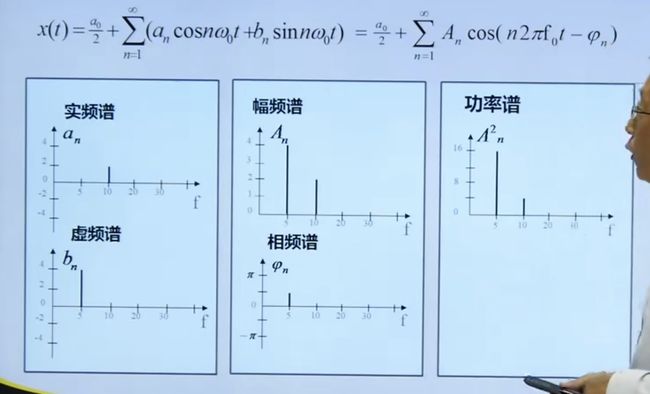
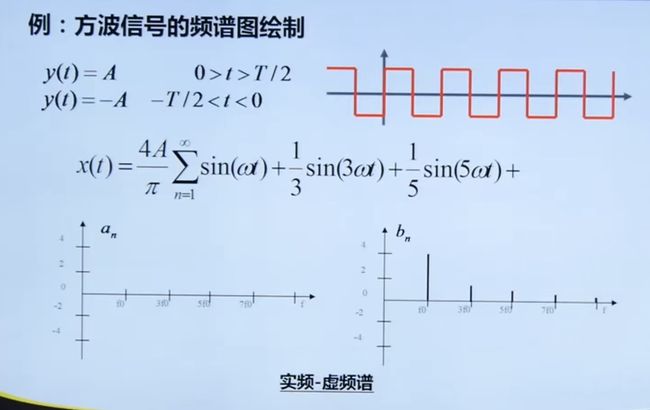
对数功率谱
对数功率谱可以使小信号的功率被展现出来。
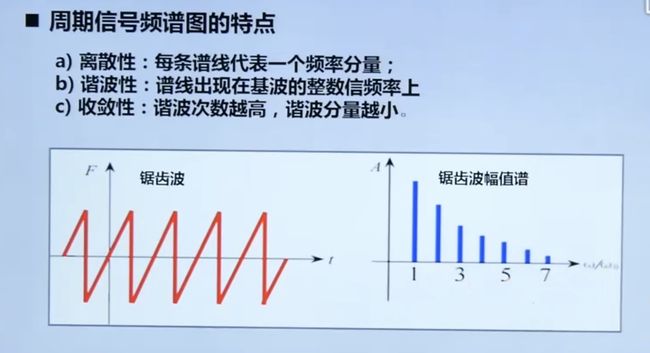
周期信号频谱图特点
- 离散性； 2. 谐波性； 3. 收敛性
4.3 数字信号频谱计算方法
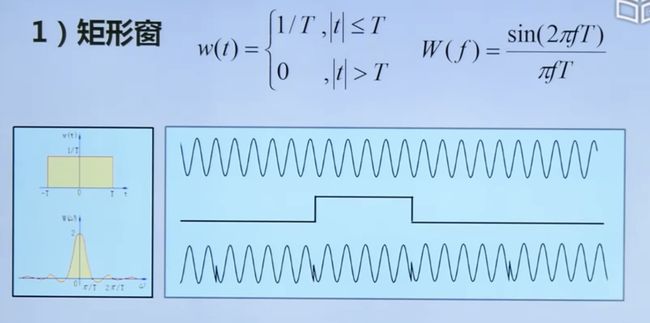
4.3.1 信号的截断与能量泄露
克服能量泄露的办法
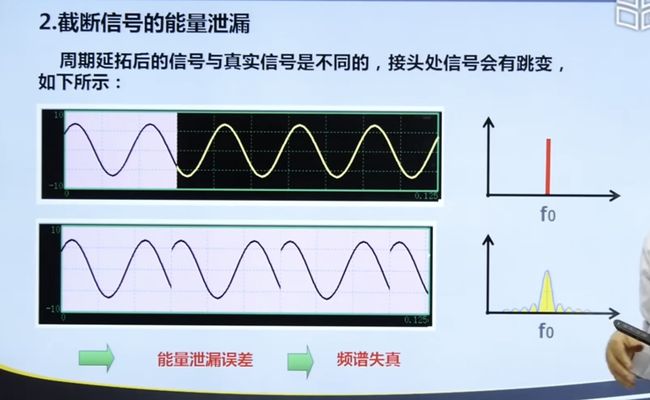
4.3.2 离散傅里叶变换（DFT）
4.3.3 快速傅里叶变换（FFT）
FFT很大程度上减小了DFT的运算复杂度，计算更快。
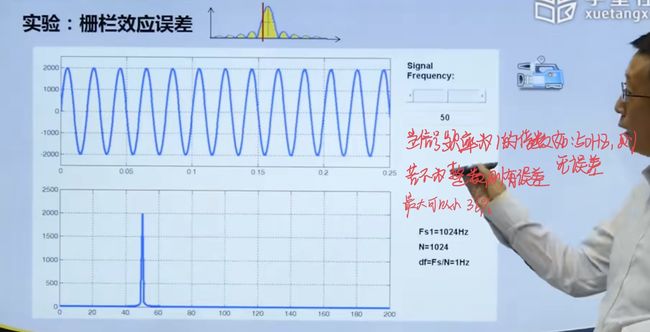
4.4 栅栏效应
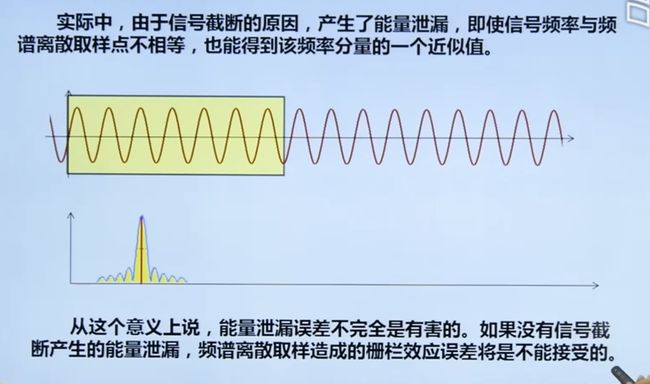
4.4.1 能量泄露与栅栏效应的关系
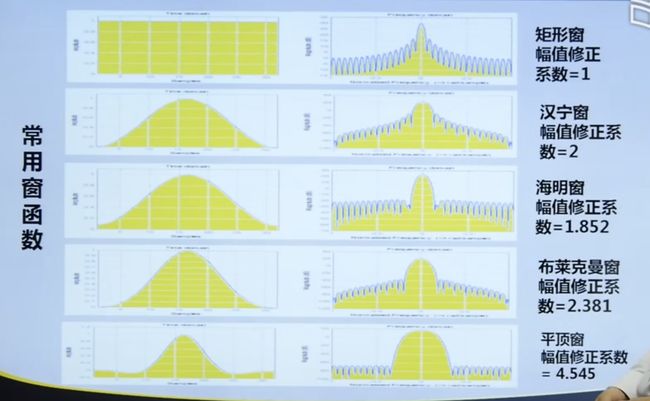
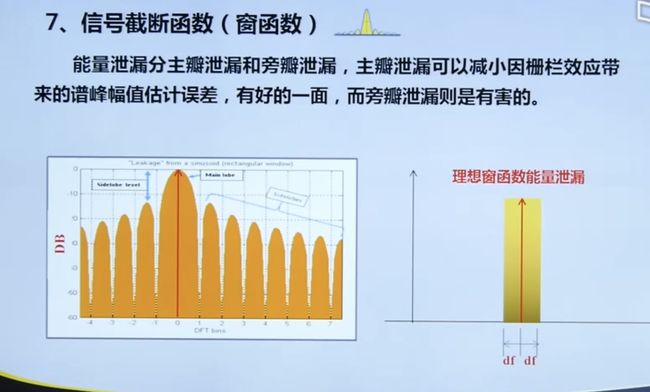
4.4.2 加窗函数
常用的窗函数
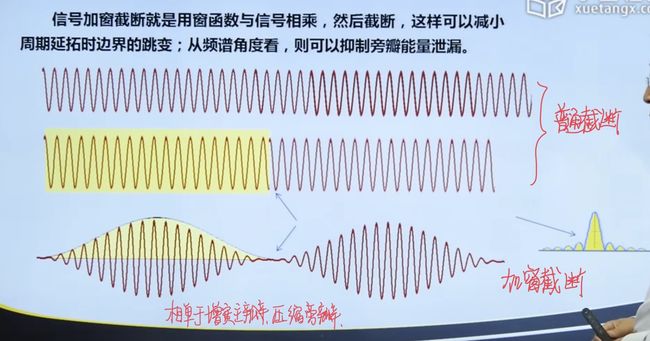
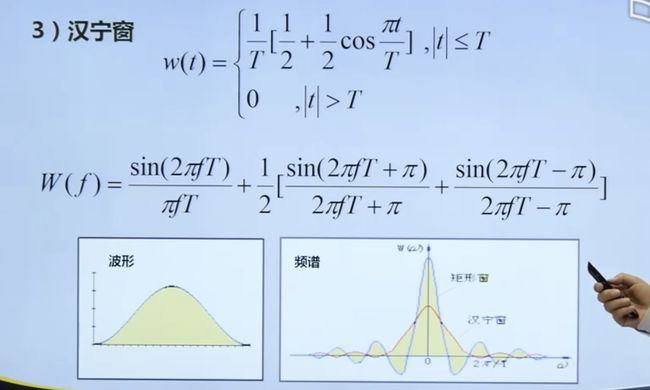
4.4.3 总结
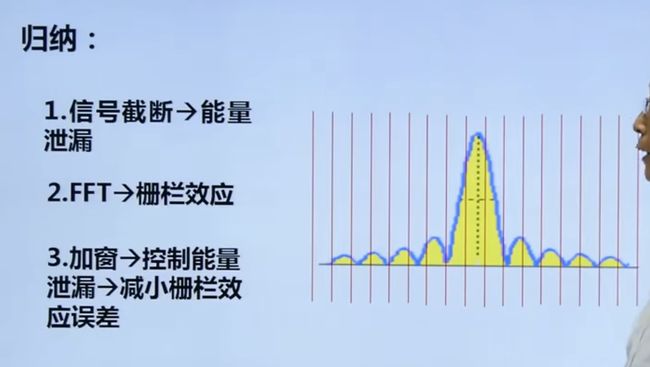
4.4 非周期信号的频谱分析
4.5 其他频谱相关知识
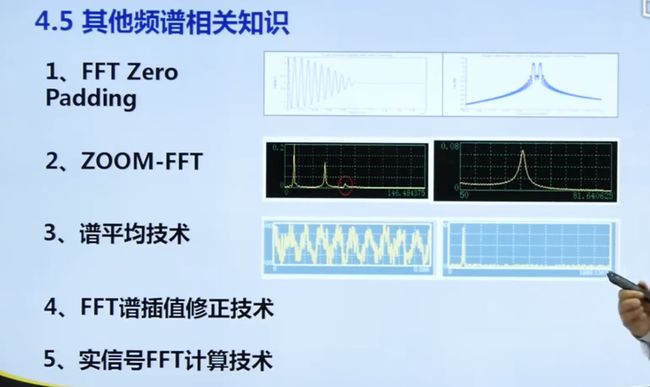
频谱分析主要用于识别信号中的周期分量，是信号分析中最常用的一种手段。
作业：
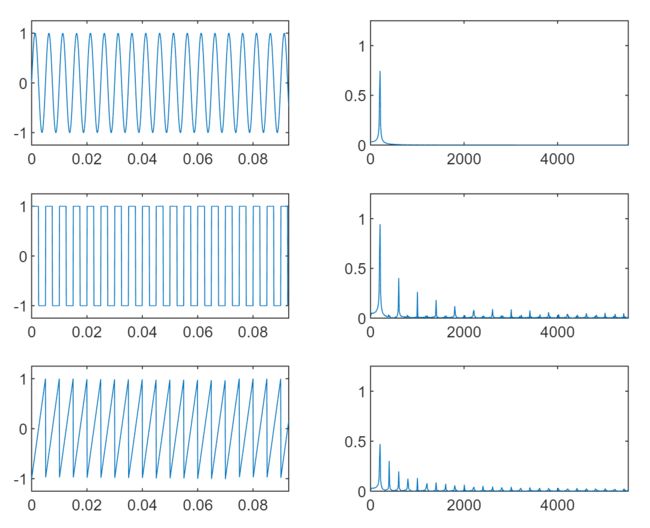
- 用11025Hz的采样率分别对幅值为10，频率为200Hz的正弦波，方波，三角波进行采样和1024点的FFT变换，并绘制出它们的信号波形和幅值谱。
Fs = 11025; % 采用频率
F = 200; % 信号频率
N = 1024; % 采样点数
dt = 1/Fs; % 采样间隔
T = dt*N; % 采样总时间
t = linspace(0,T,N);% 采样时刻
x1 = sin(2*pi*F*t);
x2 = square(2*pi*F*t);
x3 = sawtooth(2*pi*F*t);
y1 = fft(x1,N);
y2 = fft(x2,N);
y3 = fft(x3,N);
f = linspace(0,Fs/2,N/2);% x坐标转化为频率
figure
subplot(3,2,1)
plot(t,x1)
axis([-inf,inf,-1.25,1.25]);
subplot(3,2,2)
plot(f,abs(y1(1:N/2))/(N/2))
axis([-inf,inf,0,1.25]);
subplot(3,2,3)
plot(t,x2)
axis([-inf,inf,-1.25,1.25]);
subplot(3,2,4)
plot(f,abs(y2(1:N/2))/(N/2))
axis([-inf,inf,0,1.25]);
subplot(3,2,5)
plot(t,x3)
axis([-inf inf -1.25 1.25])
subplot(3,2,6)
plot(f,abs(y3(1:N/2))/(N/2))
axis([-inf,inf,0,1.25]);
结果：
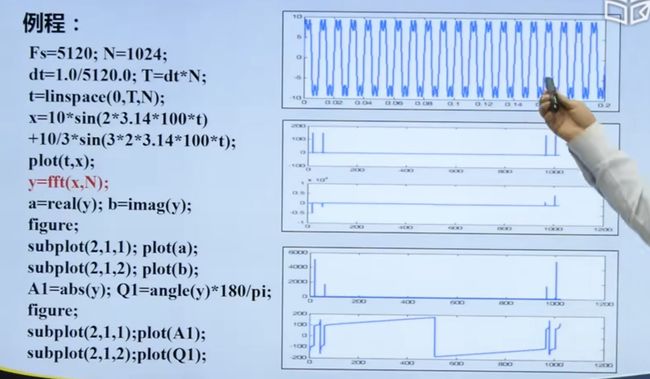
- 用5120Hz的采样率分别对幅值为1，频率为100.05Hz的正弦波信号进行采样，然后对其进行1024点的FFT变换显示信号波形和频谱；观察信号波形幅值与频谱幅值的区别，分析差异的原因。
Fs = 5120; % 采用频率
F = 100.05; % 信号频率
N = 1024; % 采样点数
dt = 1/Fs; % 采样间隔
T = dt*N; % 采样总时间
t = linspace(0,T,N);% 采样时刻
x = 10*sin(2*pi*F*t);
y = fft(x,N);
f = linspace(0,Fs/2,N/2);% x坐标转化为频率
figure
subplot(2,1,1)
plot(t,x)
axis([-inf,inf,-10.25,10.25]);
subplot(2,1,2)
plot(f,abs(y(1:N/2))/(N/2))
axis([-inf,inf,0,10.25]);
结果：
参考：
课程：
数字信号分析理论与实践——华中科技大学何岭松老师