一文速学-时间序列分析算法之一次移动平均法和二次移动平均法详解+实例代码
目录
前言
一、平滑法理论
1.时序特性
2.建模流程
二、平滑法算法
1.移动平均法
python代码:
编辑
2.二次移动平均法
与一次移动平均数关系
二次移动平均法预测公式
python代码
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
参阅:
前言
最近打算研究通彻将机器学习所有有关时间序列分析算法预测模型都讲明白清楚,在一些业务数据分析或者是数学建模需要用到强时间序列的预测模型,我们不得不学习时间序列法。严格来讲
时间序列法并不属于机器学习而是统计分析法,供预测用的历史数据资料有的变化表现出比较强的规律性,由于它过去的变动趋势将会连续到未来,这样就可以直接利用过去的变动趋势预测未来。但多数的历史数据由于受偶然性因素的影响,其变化不太规则。利用这些资料时,要消除偶然性因素的影响,把时间序列作为随机变量序列,采用算术平均、加权平均和指数平均等来减少偶然因素,提高预测的准确性。
我们将常用的时间序列分析算法平滑法模型列出:
一、平滑法理论
平滑法是对不断获得的实际数据和原预测数据给以加权平均,使预测结果更接近于实际情况的预测方法,又称光滑法或递推修正法。平滑法是趋势法或时间序列法中的一种具体方法。是为了帮助我们看清数据中的隐藏的概率形式。使具有趋势性的东西显露出来. 这里我们举个例子:
![]()
比如这张图,这是在某化学反应里,测得生成物浓度y(%)与时间t(min)的数据。我们知道浓度和时间的关系是正相关的,但是在某一时刻的数据根据点的分布我们是推测不准确的。当根据数据拟合一条时序曲线就很容易看出规律:
1.时序特性
那么基于此类时序数据我们可以发现此类数据一般用于这下面四种特性:
1.长期趋势(Trend)
2.季节变化(Season)
3.循环波动(Cyclic)
4.不规则波动(Irregular)
四种影响因素通常有两种组合方式:
一种是加法模型:Y=T+S+C+I,认为数据的发展趋势是4种影响因素相互叠加的结果
一种是乘法模型:Y=T*S*C*I,认为数据的发展趋势是4种因素相互综合的结果
2.建模流程
时序模型的建模需要我们考虑我们获取到的数据是否是时间强相关数据,而不是机器学习那种以特征为主的预测模型。通常时序模型建模步骤为:
- 数据清洗、预处理、样本均衡
- 判断是否强关联时间、确定数据是否存在周期性波动
- 确定使用时序算法模型
- 横向对比其他时序算法模型,选择最优模型
- 参数调优
二、平滑法算法
根据上述我们提到的平滑法算法我们来依次建模
1.移动平均法
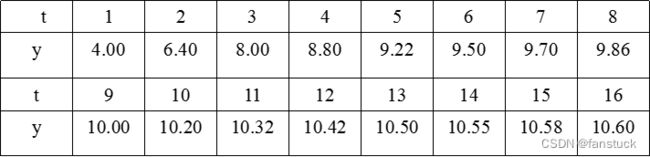
又称滑动平均法,我们以在某化学反应里,测得生成物浓度y(%)与时间t(min)的数据为例子:
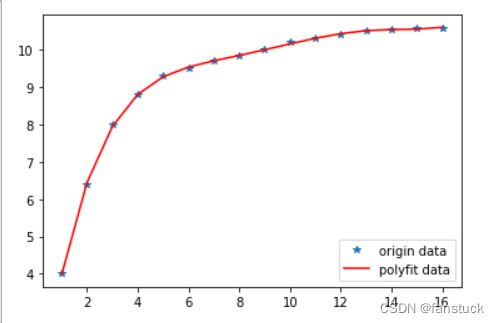
假定![]() 是随时间序列
是随时间序列![]() 发生变化的已知数据:
发生变化的已知数据:
根据上述情况我们可以得到N为16,则为![]() .将其分为若干段,以4个数据作为一段,进行滑动。
.将其分为若干段,以4个数据作为一段,进行滑动。
第一段:![]() ,
,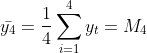 .在此
.在此![]() 为数据平均值,所有数据应在它的上下波动。那么我们可以用于推测当t=5时的数值还按前一组数值的变化幅度波动。
为数据平均值,所有数据应在它的上下波动。那么我们可以用于推测当t=5时的数值还按前一组数值的变化幅度波动。
那么我们就很好理解,当t=6时的数值按t=2到5时间段波动。
我们总结一下:一般的:
移动平均法基本上是在平均值的基础上进行预测。一般来说若经济变量在某一值上下波动情况以及升降缓慢预测效果比较好,反之误差比较大。
python代码:
x=df_metric['t']
y=df_metric['y']
def mean_shift(x,y,n):
fx=list(y[0:n])
sum=0
start=0
end=n
for i in range(0,len(y)-n):
sum=0
for j in range(start,end):
sum+=fx[j]
start+=1
end+=1
fx.append(sum/n)
return fx
fx=mean_shift(x,y,4)
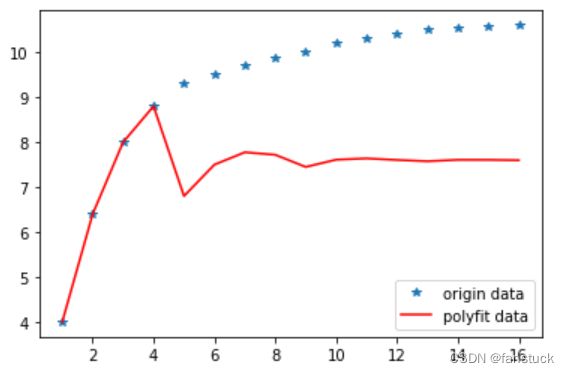
fx当时间窗口为4时我们发现移动平均法效果很差,当时序数据不进行左右浮动时而是呈现一种趋势上升时不能够很好的进行预测。这是因为末端数值已经不能很好的反应出数据走向,而作均值时又会影响最近时刻的数值点。当数据的随机因素较大时,宜选用较大的N,这样有利于较大限度地平滑由随机性所带来的严重偏差;反之当数据的随机因素较小时,宜选用较小的N,这有利于跟踪数据的变化。说到底该算法仅限于处理一段数据量不是很大且数值相对集中,变化趋势相对于平稳的数据。
2.二次移动平均法
二次移动平均是在一次平均移动的基础上再做一次移动平均。
也就是我们把时间段内是数据聚合之后,再视为成一个时间点,类似套娃。用数学语言描述就是:
![]()
递推公式![]()
![]() 为二次移动平均数
为二次移动平均数
N为分段数据个数
![]() 为以此移动平均数
为以此移动平均数
与一次移动平均数关系
一次移动平均预测对于数据变化小,近似水平变化的数据平滑作用较好。如果是线性趋势变化,形成滞后偏差![]()
线性变化如下:
![]()
有:
考虑到:![]()
则![]()
所以:
![]()
即:
类推:
则:
固:![]()
![]()
移项:![]()
有公式: ![]()
得![]()
说明用一次移动平均值模拟:真值与一次平均值存在(N-1)b_{t}/2的滞后偏差。
在线性趋势条件下:![]()
此式表明。若直接用![]() 作预测值,滞后偏差将拉大为
作预测值,滞后偏差将拉大为![]()
二次移动平均法预测公式
在线性趋势条件下,回到视为基础,用线性函数拟合假定:![]()
其中t为目前周期数,T为从目前周期t到需要预测的周期的周期个数。
![]() 为第t+T周期的预测值,
为第t+T周期的预测值,![]() 为斜率,
为斜率,![]() 为截距
为截距
若:令Y=0,得![]() 为初始值,由于当前数据为
为初始值,由于当前数据为![]() ,有
,有![]()
故选取![]() .由公式:
.由公式:![]()
代入![]() 得:
得:![]() ,
,![]()
由此构成二次移动平均预测公式。
注意:
1.预测公式是以t时刻为基准的,这个时刻可以随意选取,当选择靠近当前时刻,准确度较高。
2.因为
,
即与一次移动平均法相比较,滞后偏差(N-1)/2已补偿。
3.![]() 对应的N应一致,且二次移动值
对应的N应一致,且二次移动值![]() 不是预测值。
不是预测值。
4.二次移动平均法预测公式仅适合于线性趋势预测
5.不断的丢失信息,且N的大小一般由经验以及前期趋势确定。
python代码
def one_mean_shift(x,y,n):
fx_one=list(y[0:n])
sum=0
start=0
end=n
for i in range(0,len(y)-n):
sum=0
for j in range(start,end):
sum+=fx_one[j]
start+=1
end+=1
fx_one.append(sum/n)
return fx_one
def two_mean_shift(x,y,n):
fx_two=list(y[0:n])
M1=one_mean_shift(x,y,n)
M2=one_mean_shift(x,M1,n)
#取周期T
T=4
a = 2 * M1[len(M1) - 1] - M2[len(M2) - 1]
b = (2 / (n - 1)) * (M1[len(M1) - 1] - M2[len(M2) - 1])
print(M2)
print("a:", a, "b:", b)
# 计算 X (预测值)
X = a + b * T
return X点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
以上就是本期全部内容。我是fanstuck ,有问题大家随时留言讨论 ,我们下期见。
参阅:
时间序列平滑预测法
移动平均法和平滑法
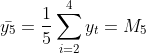
![M_{t}^{1}=[y_{t}+y_{t-1}+...+y_{t-n+1}]/N=(1/N)\sum_{t-n+1}^{t}y_{i}=\hat{y_{t+1}}](http://img.e-com-net.com/image/info8/df3543762c024759a2c61cb8c3896be8.gif)