论文复现:基于客户满意度的外卖路线优化方法(改进遗传算法)
一、论文方法简介
参考文献:Optimisation of takeaway delivery routes considering the mutual satisfactions of merchants and customers
1、模型简介
(1)VRPPDTW模型,就是带时间窗的外卖配送模型,主要约束为先取货再送货,具体约束条件描述见论文。 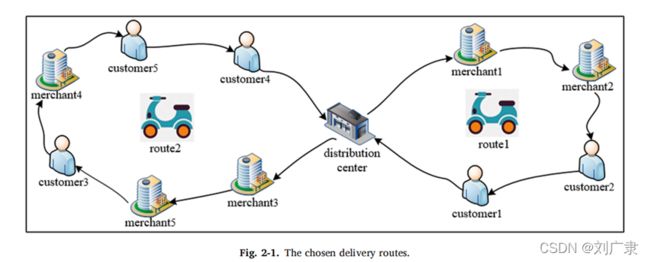


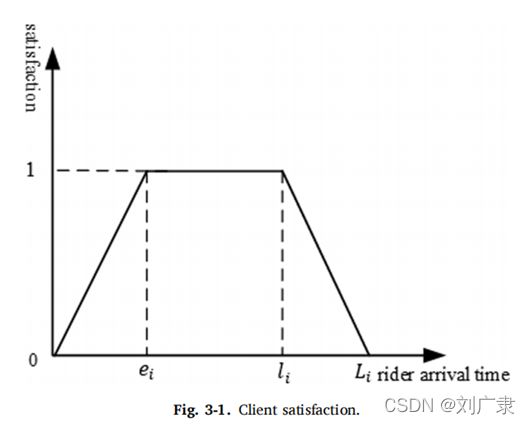
(2)客户满意度模型,即商家和顾客的满意度会随着骑手到达的时间变化,即认为骑手在[ei li]区间内到达是最佳的。
(3)目标函数,F1是电动车启动成本,固定成本;F2是骑手骑行距离成本,可变成本;F3商家和消费者的惩罚成本,与满意度有关。即算法的优化目标就是使以上三个成本总和最少。

2、算法简介
(1)采用启发式插入算法构造初始种群,加快遗传算法的收敛速度。
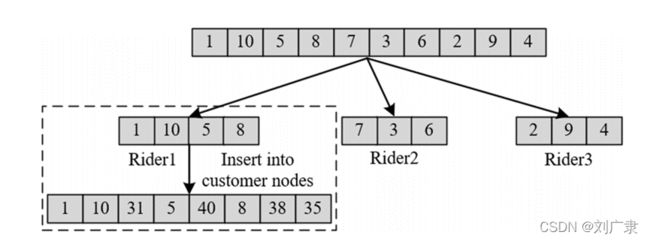
(2)采用前向连续交叉的交叉策略。
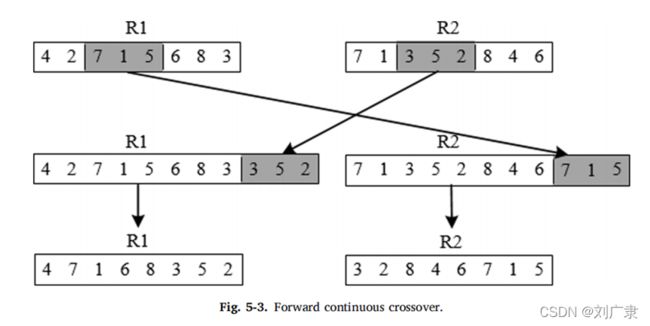
(3)采用差异突变的突变策略

(文中的差分突变方法似乎对自然数编码带来的都是不可行解?)
(4)算法流程
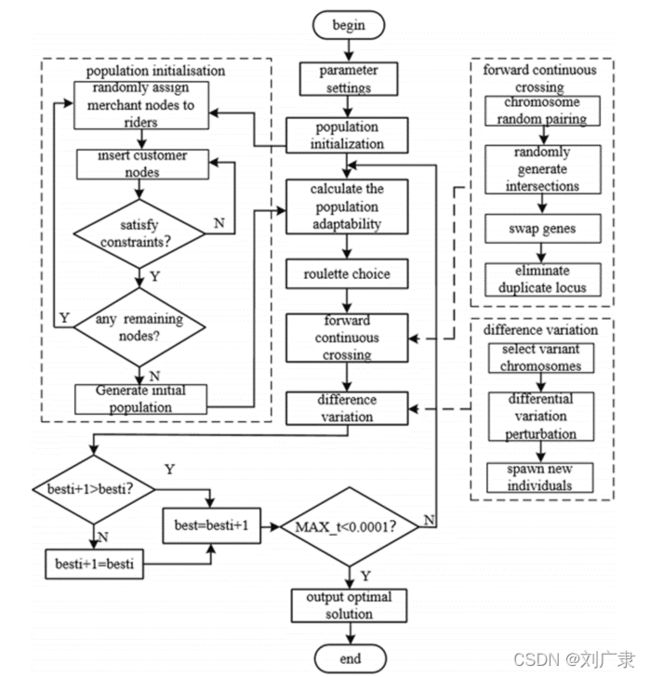
二、实验仿真
1、模型假设
以文中所给1的B1测试样例采用改进的遗传算法(IGA)进行复现,进一步简化模型,考虑30个订单由6个骑手送,主要约束条件为先取货在送货,否则设置其适应度为0(由于取0后求倒数会发生错误,可以设为0.0000001)。
2、部分过程
(1)对B1实例中商家节点和客户节点重新编号
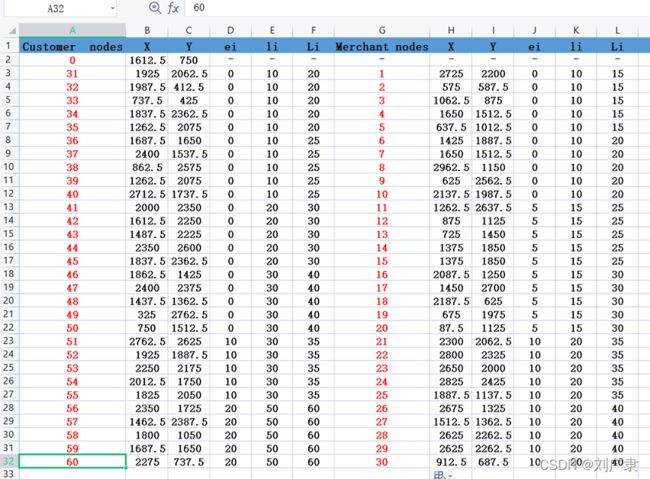
(2)启发式插入构造初始种群,可以发现初始种群都是可行解
也就是满足了先取货再送货的约束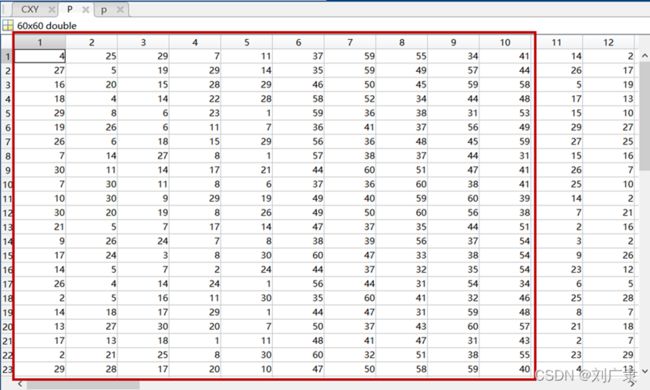
3、实验结果
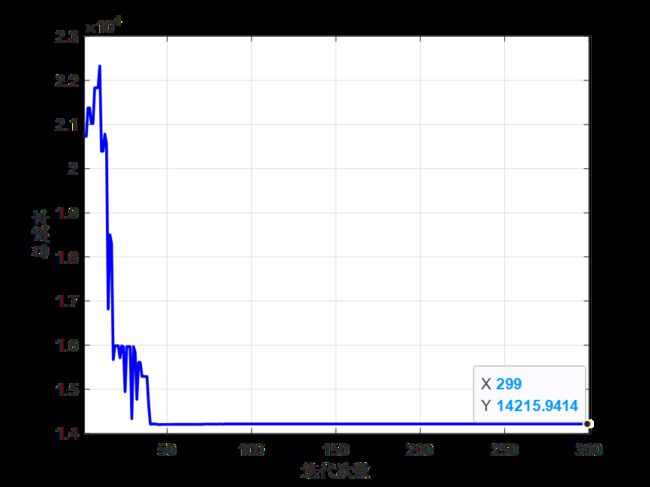
(1)迭代300次后的种群平均总成本(由于文中未给出三个成本函数的权重,故与论文中的总成本存在一定的数值差距)
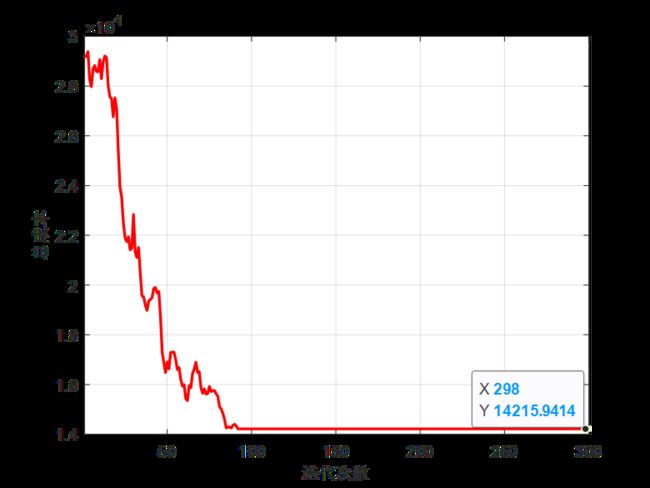
(2)论文中结果(可以发现与论文结果的算法收敛趋势差不多):
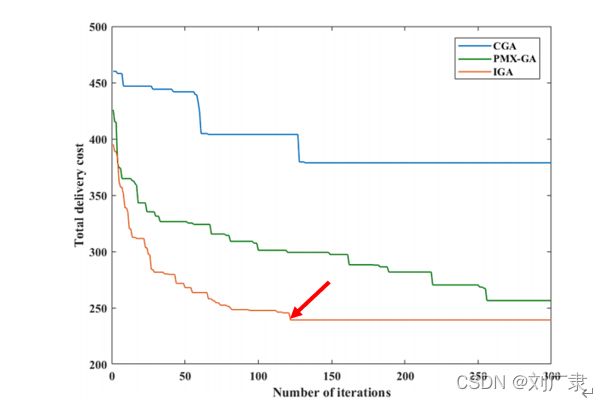
(4)迭代300次时的骑手1配送路线,蓝色圆圈为配送中心
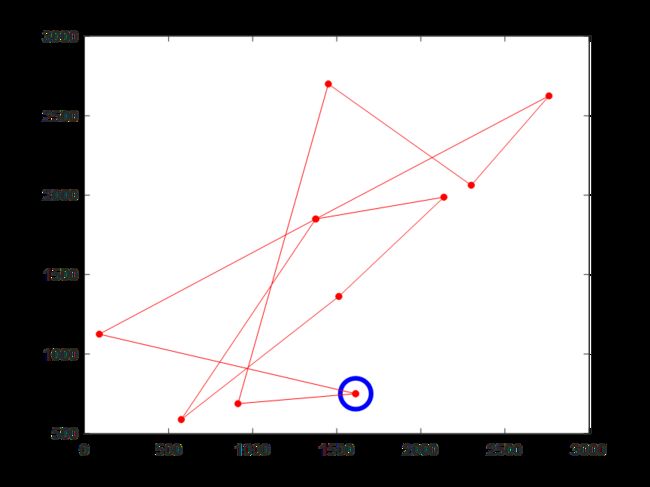
(4)迭代300次时的骑手2配送路线
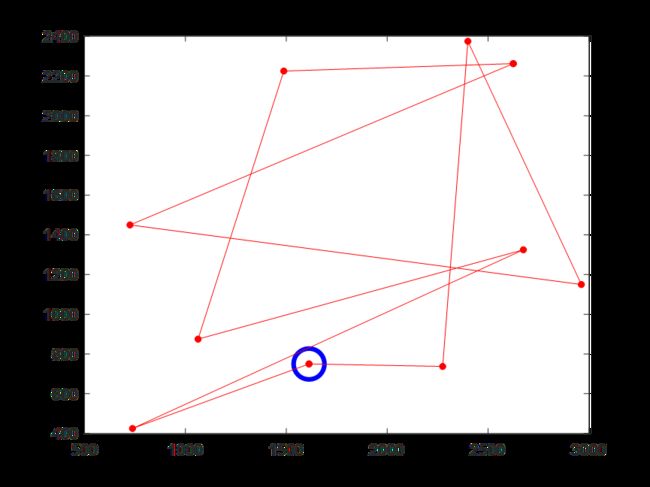
(5)迭代300次时的骑手3配送路线
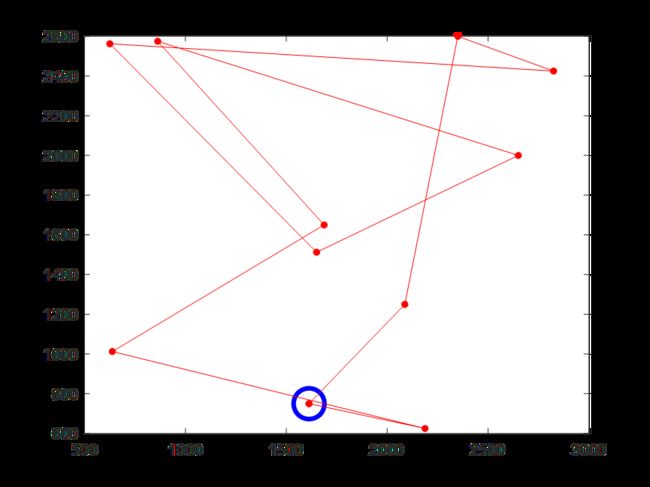
(6)迭代300次时的骑手4配送路线
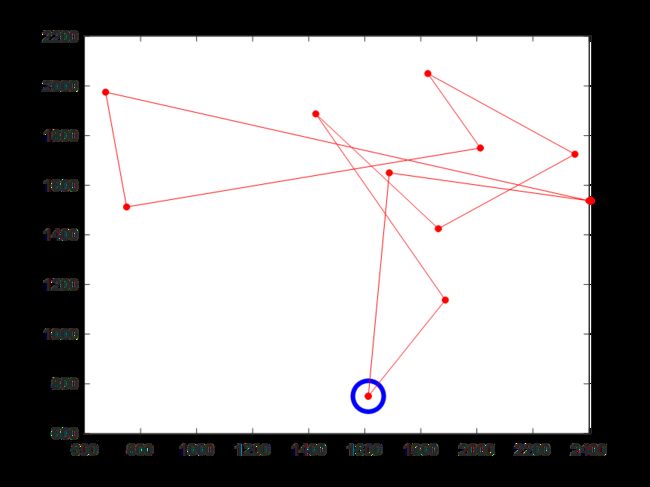
(7)迭代300次时的骑手5配送路线
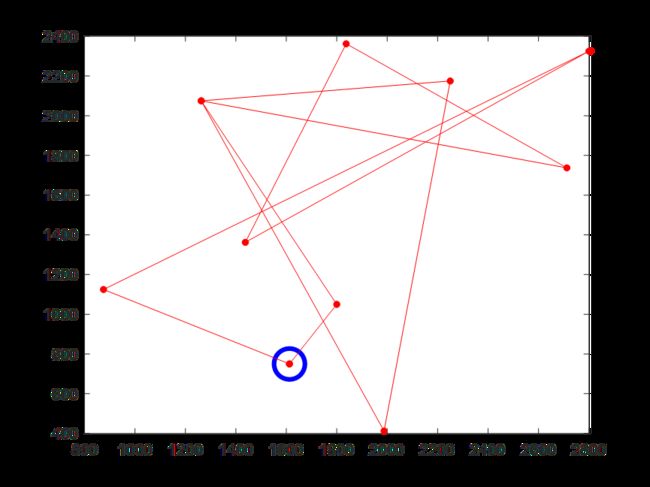
(8)迭代300次时的骑手6配送路线
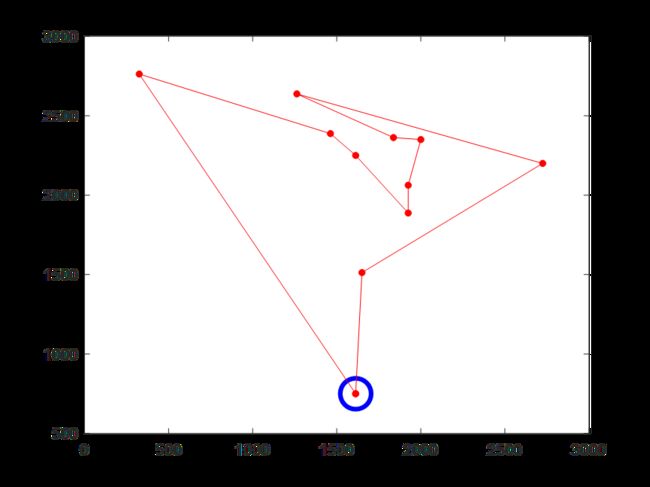
三、实验代码及说明(Matlab)
数据文件及完整项目下载地址:
gitub:https://github.com/LiuKang-coder/Improved-take-out-delivery-method-based-on-genetic-algorithm/tree/main
(求收藏!!!)
CSDN:https://download.csdn.net/download/qq_45063357/72873237
主函数:IGA.m
%%%主程序:用IGA求解30个订单,10个骑手的配送问题,假设只用了6个骑手配送,每个骑手都满载
%1:设定参数
Psize=60;%初始种群大小
% Fmax=0.0001;%最大适应度值
% Mbest=zeros(1,20);%最优个体的容量
Pc=0.8;%交叉概率
Pm=0;%突变概率
Gen=300;%迭代次数
X=zeros(Gen,Psize);%存储每代的最优个体
%2;产生初始种群
P0=F1(MN,Psize);%利用商户节点和顾客节点以及初始种群大小,采用插入式启发算法产生初始种群
%3:计算种群适应度累计概率
[Fit PP]=F2(TW,P0,XY,C0);
% GK=1;%迭代次数
%4 选择
for GK=1:Gen %%最大迭代次数
for j=1:2:Psize %%隔一个选择30次,为了保证不选择两个相同的基因型进行交
%轮盘赌法选择
Slc=Select(P0,PP);%选择的两个个体
%前向连续交叉
scr=Cross(P0,Slc,Pc);
Scnew(j,:)=scr(1,:); %交叉后产生的子代
Scnew(j+1,:)=scr(2,:);%交叉后产生的子代
%染色体突变方法
smnew(j,:)=mutation(Scnew(j,:),Pm,P0); %子程序4,对新产生的子群进行变异操作
smnew(j+1,:)=mutation(Scnew(j+1,:),Pm,P0); %子程序4,对新产生的子群进行变异操作
end
P0=smnew; %产生了新的种群
%计算新种群的适应度
[Fit PP]=F2(TW,P0,XY,C0); %计算新种群的适应度和累计概率
%记录当前代最好的适应度和平均适应度
[fmax,nmax]=max(Fit); %计算当代最大的适应度和代数
fmean=mean(Fit); %当前代的平均适应度
ymax(GK)=1/fmax; %最大的适应度
ymean(GK)=1/fmean;%平均的适应度
%记录当前代的最佳染色体个体
X(GK,:)=P0(nmax,:); %当前代的最佳染色体个体
end
%最大适应度
figure;
hand1=plot(1:GK,ymax);
set(hand1,'color','b','linestyle','-','linewidth',1.8);
xlabel('迭代次数');ylabel('总成本');xlim([1 Gen]);
% legend('最优个体的总成本');
title('Pc=0.8,Pm=0.2时最优个体的总成本')
grid on
%平均适应度
figure;
hand2=plot(1:GK,ymean);
set(hand2,'color','r','linestyle','-','linewidth',1.8)
xlabel('迭代次数');ylabel('总成本');xlim([1 Gen]);
% legend('种群的平均总成本');
title('Pc=0.8,Pm=0.2时平均总成本')
grid on
%%%画出迭代300次路线图
node=X(300,:)';
route=XY(node,:);%节点对应的坐标
for iii=1:6
route1=route(10*(iii-1)+1:10*iii,:);
route1=[C0;route1;C0];
%画连线图
figure
plot(C0(1),C0(2),'ob', 'MarkerSize',20,'linewidth',3)
hold on
plot(route1(:,1),route1(:,2),'.-r', 'MarkerSize',14)
title(['迭代300次时的骑手',num2str(iii),'的配送路线图'])
end
F1.m
%F1:插入式启发算法产生初始种群
function P=F1(MN,Psize)%P=F1(MN,60)
%%随机插入商家节点
% Psize=60;
m=size(MN,1);
for i=1:Psize;
%对MN随机排列,产生i个随机种子
PM(i,:)=randperm(m);%产生随机1-30序号排列
R1(1:5)=PM(i,1:5);
R2(1:5)=PM(i,6:10);
R3(1:5)=PM(i,11:15);
R4(1:5)=PM(i,16:20);
R5(1:5)=PM(i,21:25);
R6(1:5)=PM(i,26:30);
%%启发式插入顾客节点
%随机生成顾客节点排列
PC1=R1+30;
PC2=R2+30;
PC3=R3+30;
PC4=R4+30;
PC5=R5+30;
PC6=R6+30;
%对PC随机排列,产生i个随机种子
ID1(1:5)=randperm(5);%产生顾客随机序号
ID2(1:5)=randperm(5);%产生顾客随机序号
ID3(1:5)=randperm(5);%产生顾客随机序号
ID4(1:5)=randperm(5);%产生顾客随机序号
ID5(1:5)=randperm(5);%产生顾客随机序号
ID6(1:5)=randperm(5);%产生顾客随机序号
NPC1(1:5)=PC1(ID1(1:5));
NPC2(1:5)=PC2(ID2(1:5));
NPC3(1:5)=PC3(ID3(1:5));
NPC4(1:5)=PC4(ID4(1:5));
NPC5(1:5)=PC5(ID5(1:5));
NPC6(1:5)=PC6(ID6(1:5));
NR1(i,1:10)=[R1 NPC1];
NR2(i,1:10)=[R2 NPC2];
NR3(i,1:10)=[R3 NPC3];
NR4(i,1:10)=[R4 NPC4];
NR5(i,1:10)=[R5 NPC5];
NR6(i,1:10)=[R6 NPC6];
end
NP=[NR1 NR2 NR3 NR4 NR5 NR6];
P=NP;
End
F2.m
%%计算适应度和累计概率
function [Fit PP]=F2(TW,P0,XY,C0)
%计算每个订单的距离长度
[m,n]=size(P0);
%%%求每条染色体的适应度
for i=1:m
p1=P0(i,:);%每条染色体
D=zeros(1,m);%总距离
T=zeros(1,m);%总时间成本
for j=1:10:51 %第j个骑手
d(1)=Dist(C0,XY(p1(j),:));%起点到第一个节点
d(11)=Dist(XY(p1(j+9),:),C0);%最后一个节点到终点
for jn=2:10 %第j个骑手对应的节点
%%计算距离
d(jn)=Dist(XY(p1(j+jn-2),:),XY(p1(j+jn-1),:))/1000;
end
dd=sum(d);%每个骑手对应的总距离
D(i)=0.1*(D(i)+dd);%订单总距离:km,C2未告诉,取0.2
%%求解时间窗损耗
tt=Ftime(TW,p1,d,j);%每个骑手对应的惩罚时间,10个节点
T(i)=T(i)+tt;%订单总惩罚时间
end
%%计算每条染色体的总成本,分别为启动成本、骑行成本、惩罚时间成本
f(i)=0.24*100+0.12*D(i)+0.64*T(i);%总成本
Fit(i)=1/f(i);%适应度取倒数
end
%%将不满足约束条件的染色体个体的适应度设为0,由于0取倒数会存在问题,这里设为0.000001
for i=1:m %整个种群
p1=P0(i,:);%每条染色体
for id=1:30
IDm=find(p1==id);%商家节点序号
IDc=find(p1==(id+30));%顾客节点序号
if IDc<IDm %顾客节点在商家节点前面,令适应度为0.00000001
Fit(i)=0.00000001;
break;
end
end
end
%%%求累计概率PP
%求总适应度
PS=sum(Fit);
PP(1)=Fit(1)/PS;
for ii=2:m
PP(ii)=PP(ii-1)+Fit(ii)/PS;%累计概率
end
PP=PP';
end
Ftime.m
function tt=Ftime(TW,p1,d,j)
% T=0;%总惩罚时间
%%%每个客户节点的服务时间为2分钟
%骑行速度为10 km/60min
%骑行到每个节点的时间为距离除以速度,骑行到第一个节点是没有服务时间的
tt(1)=d(1)*6;%1km骑6分钟
%从第2个节点到其它11个节点的骑行时间
for jj=1:10 %jj对应第jj个客户节点
t(jj)=2+d(jj)*6;%骑行时间
ta(jj)=sum(t);%到达每个节点的时间
tcost(jj)=0.1*(max(ta(jj)-TW(p1(jj-1+j),1),0)+max(TW(p1(jj-1+j),2)-ta(jj),0));%%C3为告诉,取0.1
end
tt=sum(tcost);%总惩罚时间
end
Select.m
%新种群选择操作
function Slc=Select(P0,PP);%%输入种群,累计概率
%从种群中选择两个个体
for i=1:2 %一下选择两个个体
r=rand; %产生一个(0,1)随机数
prand=PP-r;%所有元素减r
j=1;
while prand(j)<0 %
j=j+1; %j所在的累计概率是第一个大于r的,即多次生成r,就能选择累计概率最接近r的个体,即是轮盘赌法选择
end
Slc(i)=j; %第一次和第二次选中的个体代号,为了方便交叉
end
mutation.m
%新种群变异操作
function snnew=mutation(Scnew,Pm,P0);%一下输入一个子群和变异概率
[m,n]=size(P0);;%子群位长
snnew=Scnew;%%变异后的子群
pmm=IfCroIfMut(Pm); %根据变异概率决定是否进行变异操作,1则是,0则否,类似交叉 %子程序7
if pmm==1
chb1=round(rand*(m-1))+1; %在[1,60]范围内随机产生一个变异位
chb2=round(rand*(m-1))+1; %在[1,60]范围内随机产生一个变异位
%交换两个变异位
mm=snnew(chb1:chb1+1);
snnew(chb1)=snnew(chb2:chb2+1);%交换
snnew(chb2)=mm;
end
end
Cross.m
%前向连续交叉
function Scr=Cross(P0,Slc,Pc);%初始种群,选择的个体,交叉概率
[m,n]=size(P0);
pcc=IfCroIfMut(Pc); %根据交叉概率决定是否进行交叉操作,1则是,0则否
if pcc==1 %进行交叉
chb=round(rand*(m-2))+1; %在[1,59]范围内随机产生一个交叉位,rand为【0,1】之间的随机数,chb后面才交叉,故到m-1
Scro(1,:)=[P0(Slc(1),:) P0(Slc(2),chb+1:m)];%%在chb,前一部分保留,后一部分交叉
Scro(2,:)=[P0(Slc(2),:) P0(Slc(1),chb+1:m)];%%在chb,前一部分保留,后一部分交叉
%%%删除重复节点
S1=fliplr(Scro(1,:));%倒序
S2=fliplr(Scro(2,:));%倒序
S1=unique(S1,'stable');%删除重复节点
S2=unique(S2,'stable');%删除重复节点
Scr(1,:)=fliplr(S1);
Scr(2,:)=fliplr(S2);
else
Scr(1,:)=P0(Slc(1),:); %不进行交叉
Scr(2,:)=P0(Slc(2),:); %进行交叉
end
Dist.m
%求欧几里得距离函数dist
function y=Dist(x1,x2) %输入坐标
y=sqrt((x2(1)-x1(1))^2+(x2(2)-x1(2))^2);
end
IfCroIfMut.m
%判断遗传运算是否需要进行交叉或变异
function pcc=IfCroIfMut(mutORcro); %输入交叉概率
test(1:100)=0;
L=round(100*mutORcro);%l=L,概率取整
test(1:L)=1;
n=round(rand*99)+1;%%随机生成1到100之间的数
pcc=test(n); %以90%的概率判断是否进行交叉