《实战》 用Tensorflow 实现线性回归
用Tensorflow 实现线性回归
- 1.生成样本数据x_data,和y_data
- 2. 构建预测模型
- 3.迭代进行训练,获取最佳的w和b
1.生成样本数据x_data,和y_data
本次案例主要是通过学习的tensorflow实现找到最佳的w和b的拟合曲线
首先通过随机函数生成一个在一定范围内的随机数,作为一个x
构建目标函数的f(x),通过f(x)去拿到一个实际的一个y的值
我们先假设这个目标函数的表达式为 y = 0.3*x + 0.1 ,通过梯度下降,拟合出最合适的w和b
import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
x_num = 1000
vector = [] #保存x和y
for i in range(x_num):
x1 = np.random.normal(0.0,0.05)
y1 = x *0.3 + 0.1 + np.random.normal(0.0,0.03) #给y加一个随机数,添加点苦难度
vector.append([x1,y1])
这个时候,我们就已经构建出来了,x和y 的值都保留在vector的列表里面,所以我们要去里面拿到我们的x和y的值
#取出 x和 y
x_data = [v[0] for v in vector]
y_data = [v[1] for v in vector]
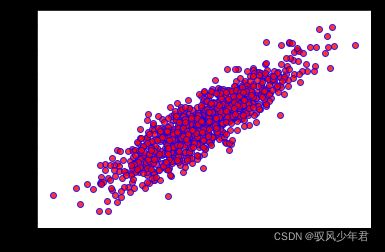
plt.scatter(x_data,y_data,c='r',alpha=0.8,edgecolors='b')
plt.show()
2. 构建预测模型
构建预测模型,预测模型的参数,要用tf.Veriable 来构建W和一个b的值。
一开始的值设置一个随机数就可以
W = tf.Variable(tf.random_normal([1],-1.0,1.0),name='W') #随机生成一个-1.0到1.0之间的数作为W
b = tf.Variable(tf.zeros([1]),name='b')
y = W* x_data + b
对于回归函数的损失值可以用平方的值进行计算。
构建出一个预测模型后,就需要计算一个损失值,获取每次将计算得到的损失值交给优化器
优化器里面需要定义一个学习率,一般学习率可以设置的小一点,但是这次的实战结果wb,比较简单,所以可以设置的大一点。
loss = tf.reduce_mean(tf.square(y - y_data),name = 'loss')
optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(loss)
3.迭代进行训练,获取最佳的w和b
因为w和b,是一个自定义的变量参数,所以需要对变量进行一个初始化。
sess = tf.Session()
#全局初始化
init = tf.global_variables_initializer()
sess.run(init)
print('W:',sess.run(W),'b:',sess.run(b)) #当前的一个w和b
通过迭代计算,不断的优化w和一个b
for i in range(30):
sess.run(train)
print('W:',sess.run(W),'b:',sess.run(b),'loss:',sess.run(loss))
W: [ 0.09984849] b: [ 0.30040082] loss: 0.00083885
W: [ 0.10006099] b: [ 0.30040208] loss: 0.000838772
W: [ 0.10021279] b: [ 0.30040294] loss: 0.000838732
W: [ 0.10032122] b: [ 0.30040357] loss: 0.000838712
W: [ 0.10039867] b: [ 0.30040401] loss: 0.000838702
W: [ 0.100454] b: [ 0.30040434] loss: 0.000838697
W: [ 0.10049352] b: [ 0.30040458] loss: 0.000838694
W: [ 0.10052175] b: [ 0.30040473] loss: 0.000838693
W: [ 0.10054192] b: [ 0.30040485] loss: 0.000838692
W: [ 0.10055632] b: [ 0.30040494] loss: 0.000838691
W: [ 0.10056661] b: [ 0.300405] loss: 0.000838692
W: [ 0.10057396] b: [ 0.30040506] loss: 0.000838691
W: [ 0.10057922] b: [ 0.30040509] loss: 0.000838691
W: [ 0.10058296] b: [ 0.30040509] loss: 0.000838691
W: [ 0.10058565] b: [ 0.30040511] loss: 0.000838691
W: [ 0.10058756] b: [ 0.30040511] loss: 0.000838691
W: [ 0.10058893] b: [ 0.30040511] loss: 0.000838691
W: [ 0.1005899] b: [ 0.30040514] loss: 0.000838691
W: [ 0.1005906] b: [ 0.30040514] loss: 0.000838691
W: [ 0.1005911] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059146] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059171] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059189] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059202] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059211] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059217] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059222] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059226] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059228] b: [ 0.30040514] loss: 0.000838691
W: [ 0.10059229] b: [ 0.30040514] loss: 0.000838691
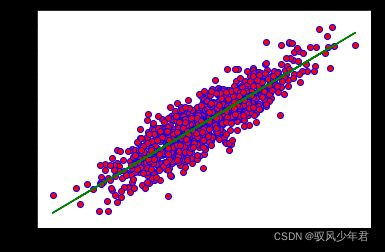
可以绘制一个线性的拟合曲线
plt.scatter(x_data,y_data,c='r',edgecolors='b')
plt.plot(x_data,sess.run(W) * x_data + sess.run(b),c='g')
plt.show()