深度学习之卷积神经网络(12)深度残差网络
深度学习之卷积神经网络(12)深度残差网络
- ResNet原理
- ResBlock实现
AlexNet、VGG、GoogleLeNet等网络模型的出现将神经网络的法阵带入了几十层的阶段,研究人员发现网络的层数越深,越有可能获得更好的泛化能力。但是当模型加深以后,网络变得越来越难训练,这主要是由于梯度弥散和梯度爆炸现象造成的。在较深层数的神经网络中,梯度信息由网络的末层传向网络的首层时,传递的过程中会出现梯度接近于0或梯度值非常大的现象。网络层数越深,这种现象可能会越严重。
那么怎么解决深层神经网络的梯度弥散和梯度爆炸现象呢?一个很自然的想法是,既然浅层神经网络不容易出现这些梯度现象,那么就可以尝试给深层神经网络添加一种 回退到浅层神经网络的机制。当深层神经网络可以轻松地回退到浅层神经网络时,深层神经网络可以获得与浅层设立相当的模型性能,而不至于更糟糕。
通过在输入和输出之间添加一条直接连接的 Skip Connection可以让神经网络具有回退的能力。以VGG13深度神经网络为例,假设观察到VGG13模型出现梯度弥散现象,而10层的网络模型并没有观测到梯度弥散现象,那么可以考虑在最后的两个卷积层添加Skip Connection,如下图所示。通过这种方式,网络模型可以自动选择是否经由这两个卷积层完成特征变换,还是直接跳过这两个卷积层而选择Skip Connection,亦或结合两个卷积层和Skip Connection的输出。
2015年,微软亚洲研究院何凯明等人发表了基于Skip Connection的深度残差网络(Residual Nerual Network,简称ResNet)算法[1],并提出了18层、34层、50层、101层、152层的ResNet-18、ResNet-34、ResNet-50、ResNet-101和ResNet-152等模型,甚至成功训练出层数达到1202层的极深神经网络。ResNet在ILSVRC2015挑战赛ImageNet数据集上的分类、检测等任务上面均获得了最好性能,ResNet论文至今已经获得超25000的引用量,可见ResNet在人工智能行业的影响力。
[1] K. He, X. Zhang, S. Ren 和 J. Sun, “Deep Residual Learning for Image Recognition,” CoRR, 卷 abs/1512.03385, 2015.
ResNet原理
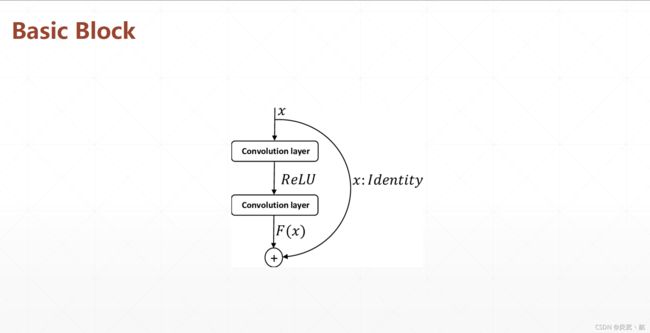
ResNet通过在卷积层的输入和输出之间添加Skip Connec-tion实现层数回退机制,如下图所示,输入 x \boldsymbol x x通过两个卷积层,得到特征变换后的输出 F ( x ) \mathcal F(\boldsymbol x) F(x),与输入 x \boldsymbol x x进行对应元素的相加运算,得到最终输出 H ( x ) \mathcal H(\boldsymbol x) H(x):
H ( x ) = x + F ( x ) \mathcal H(\boldsymbol x)=\boldsymbol x+\mathcal F(\boldsymbol x) H(x)=x+F(x)
H ( x ) \mathcal H(\boldsymbol x) H(x)叫做残差模块(Residual Block,简称ResBlock)。由于被Skip Connection包围的卷积神经网络需要学习映射 F ( x ) = H ( x ) − x \mathcal F(\boldsymbol x)=\mathcal H(\boldsymbol x)-\boldsymbol x F(x)=H(x)−x,故称为残差网络。
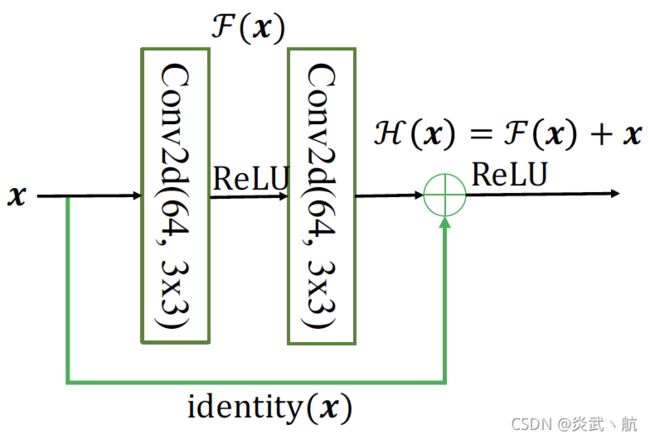
为了能够满足输入 x \boldsymbol x x与卷积层的输出 F ( x ) \mathcal F(\boldsymbol x) F(x)能够相加运算,需要输入 x \boldsymbol x x的shape与 F ( x ) \mathcal F(\boldsymbol x) F(x)的shape完全一致。当出现shape不一致时,一般通过在Skip Connection上添加额外的卷积运算缓解将输入 x \boldsymbol x x变换到与 F ( x ) \mathcal F(\boldsymbol x) F(x)相同的shape,如下图中 identity ( x ) \text{identity}(\boldsymbol x) identity(x)函数所示,其中 identity ( x ) \text{identity}(\boldsymbol x) identity(x)以 1 × 1 1×1 1×1的卷积运算居多,主要英语调整输入的通道数。
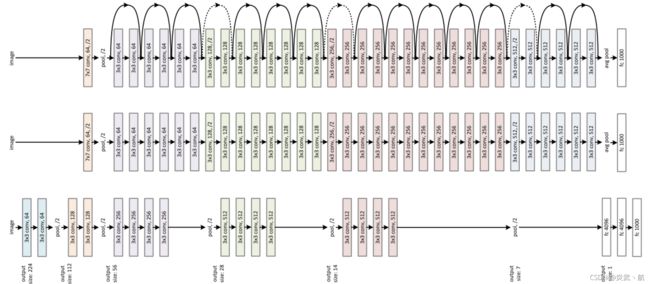
如下图所示,对比了34层的深度残差网络、34层的普通深度网络以及19层的VGG网络结构。可以看到,深度残差网络通过堆叠残差模块,达到了较深的网络层数,从而获得了训练稳定、性能优越的深层网络模型。
ResBlock实现
深度残差网络并没有增加新的网络层类型,只是通过在输入和输出之间添加一条Skip Connection,因此并没有针对ResNet的底层实现。在TensorFlow中通过调用普通卷积层即可实现残差模块。
首先创建一个新类,在初始阶段创建残差块中需要的卷积层、激活函数层等,首先新建 F ( x ) \mathcal F(\boldsymbol x) F(x)卷积层,代码如下:
class BasicBlock(layers.Layer):
# 残差模块
def __init__(self, filter_num, stride=1):
super(BasicBlock, self).__init__()
# 第一个卷积单元
self.conv1 = layers.Conv2D(filter_num, (3, 3), strides=stride, padding='same')
self.bn1 = layers.BatchNormalization()
self.relu = layers.Activation('relu')
# 第二个卷积单元
self.conv2 = layers.Conv2D(filter_num, (3, 3), strides=1, padding='same')
self.bn2 = layers.BatchNormalization()
其中:
__init__(self, filter_num, stride=1)函数为初始化函数,filter_num为卷积核的数量,stride=1表示不对输入进行下采样;strides=stride, padding='same'表示可以直接得到输入、输出同大小的卷积层;layers.BatchNormalization()表示标准化层;
当 F ( x ) \mathcal F(\boldsymbol x) F(x)的形状与 x \boldsymbol x x不同时,无法直接相加,我们需要新建 identity ( x ) \text{identity}(\boldsymbol x) identity(x)卷积层,来完成 x \boldsymbol x x的形状转换。紧跟上面代码,实现如下:
if stride != 1:# 通过1x1卷积完成shape匹配
self.downsample = Sequential()
self.downsample.add(layers.Conv2D(filter_num, (1, 1), strides=stride))
else:# shape匹配,直接短接
self.downsample = lambda x:x
上述代码表示如果stride(即步长)如果不为1的话,那么输出与输入的shape不相同,那么此时我们就需要新建 identity ( x ) \text{identity}(\boldsymbol x) identity(x)卷积层,来完成 x \boldsymbol x x的形状转换,使之与输入的shape相同。
在向前传播时,只需要将 F ( x ) \mathcal F(\boldsymbol x) F(x)与 identity ( x ) \text{identity}(\boldsymbol x) identity(x)相加,并添加ReLU激活函数即可。向前计算函数代码如下:
def call(self, inputs, training=None):
# [b, h, w, c],通过第一个卷积单元
out = self.conv1(inputs)
out = self.bn1(out)
out = self.relu(out)
# 通过第二个卷积单元
out = self.conv2(out)
out = self.bn2(out)
# 通过identity模块
identity = self.downsample(inputs)
# 2条路径输出直接相加
output = layers.add([out, identity])
output = tf.nn.relu(output) # 激活函数
return output