【机器学习】21天挑战赛学习笔记（一）

​
​

活动地址：CSDN21天学习挑战赛

学习的最大理由是想摆脱平庸，早一天就多一份人生的精彩；迟一天就多一天平庸的困扰。各位小伙伴，如果您：
想系统/深入学习某技术知识点…
一个人摸索学习很难坚持，想组团高效学习…
想写博客但无从下手，急需写作干货注入能量…
热爱写作，愿意让自己成为更好的人

学习日记

目录

学习日记

1，学习知识点

2，学习的收获

​1.回归的基本思想

2.损失函数

3.最小二乘法

4.梯度下降法

5.泛化

6.过拟合与欠拟合

7.MSE和RMSE

 8.MAE和MAPE

 9.正则项

---

1，学习知识点

1.回归的基本思想

2.损失函数

3.最小二乘法

4.梯度下降法

5.泛化

6.过拟合与欠拟合

7.MSE和RMSE

8.MAE和MAPE

9.正则项

2，学习的收获

根据以上的学习知识点进行学习总结，总结知识点如下：

​1.回归的基本思想

回归是对一个或多个自变量和因变量之间的关系进行建模，求解的一种统计方法。很多模型都是在他的基础上建立的，任何一个复杂模型，其内部可能会隐藏着许多回归模型。

2.损失函数

损失函数的作用:衡量模型模型预测的好坏。再简单一点说就是:损失函数就是用来表现预测与实际数据的差距程度。

①直接法

直接法就是给出优化问题的最优解，并不是所有的优化问题都可以用直接法得到最优解，如果要使用直接法，损失函数需要满足两个条件：

（a）损失函数为凸函数；

（b）损失函数为解析解，即通过严格的公式所求得的解。

凸函数的定义：

设函数为凸函数，当且仅当对定义域中任意两点和任意实数，总有：

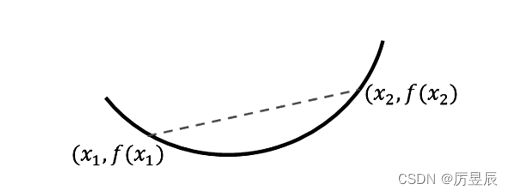
通过图像直观来看，凸函数上任意浪点连接而成的虚线，永远在凸函数曲线的上方，如图所示：

 由上述定义，我们可以了解到，如果一个函数是凸函数，那么我们可以求解出它的全局最优解，但如果一个函数是非凸的，那么我们可能求出的是它的局部最优解。

补充：

在数学上，有两个概念，一个是local optimal solution（局部最优解），一个是global optimal solution（全局最优解）。

⭐全局最优解

指的是针对一定条件/环境下的一个问题/目标，若一项决策和所有解决该问题的决策相比是最优的。

⭐局部最优解

指的是对于一个问题的解在一定范围或区域内最优，或者说解决问题或达成目标的手段在一定范围或限制内最优。

②迭代法

很多情况中，我们的损失函数为非凸函数，因此，我们可以选择使用迭代法求解。迭代法是一种不断用变量的旧值递推新值的过程，即迭代的用旧值修正对最优解的估计。

小批量梯度下降法的过程如下：

（a）确定求解的模型参数为α、β；

（b）定义小批量梯度下降法的损失函数；

（c）求解梯度，并定义递推关系；

（d）迭代，迭代完成输出最后的模型参数。

 多元回归基本原理

矩阵的知识补充：

①加法

矩阵的加法满足下列运算律，（A、B、C都是同型矩阵）

A+B=B+A

(A+B)+C=A+(B+C)

②减法 

与加法的运算相反。

③数乘

矩阵的数乘满足以下运算律：

 

 【注意】矩阵的加减法和矩阵的数乘合称矩阵的线性运算。

矩阵的定义：

由m×n个数aij排成的m行n列的数表称为m行n列的矩阵，简称m×n矩阵。

矩阵的基本运算：

加法、减法、数乘、转置、共轭、共轭转置。

---

在现实生活中，我们要分析的不只是一个，而是多个自变量与因变量之间的关系，对于这种预测任务，我们可以采用多元线性回归。

3.最小二乘法

定义：

最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小 [1]  [6-7]  。

最小二乘法还可用于曲线拟合，其他一些优化问题也可通过最小化能量或最大化熵用最小二乘法来表达。

原理：

1.最小二乘法（也称为最小平法）是一种最优的数学方法。它是将错误的平方减到最少，并找到最优的功能。采用最小二乘方法，可以方便地求出未知数据，并使其与真实资料的平方和最小。同时，最小二乘方法也可以进行曲线拟合。其它的优化问题可以用最小二乘方法表示，即使能量最少或熵最大。

2.最小二乘多项式曲线拟合，它不需要在给定的 m个点上准确地通过，而只需要在曲线 y= f （x）上进行近似。

3.最小二乘，是求一条直线，它使得各数据点之间的距离平方和最小。所以，只需求出与其最小值相应的线性方程的参量。

---

对于回归问题，我们可以直接利用最小二乘法得到最优解。

【注意】又是自变量之间存在不完全多重共现性，此时我们可以用梯度下降法，或者添加正则项的方式解决这些问题。

4.梯度下降法

 在优化问题求解时，经常会使用泰勒展开来近似代替目标函数，梯度下降法就是利用一阶泰勒展开，从而最小化损失函数的方法。

在梯度下降法中，由于每次迭代带入损失函数中样品个数的不同，我们又可将其分为：

批量梯度下降法（BGD）

小批量梯度下降法（MBGD）

随机梯度下降法（SGD）

5.泛化

①由具体的，个别的扩大为一般的；

②当某一反应与某种刺激形成条件联系后，这一反应也会与其他类似的刺激形成某种角度的条件联系，其过程称为泛化。

6.过拟合与欠拟合

过拟合：

 训练集上表现好，但在测试集上表现差的现象。

欠拟合：

在训练集上表现差，但在测试集上表现好的现象。

7.MSE和RMSE

 在回归分析中，最常用的评价模型的指标就是均方差MSE以及均方根误差RMSE。

均方差（MSE）：标准差，是离均差平方的算数平均数（方差），用表示；

标准差是方差的算术平方根，标准差能反映一个数据集的离散程度。平均数相同的两组数据标准差未必相同。

 

 8.MAE和MAPE

平均绝对误差MAE是将预测误差取绝对值后的平均误差，平均百分比误差MAPE则消除了因变量单位的影响，反映了误差大小的相对值。

 

 9.正则项

 在建模时，我们总是希望自己的模型能够尽量在训练集上取得较高的精度，又希望模型有好的泛化能力，这时，我们可以通过给损失函数添加正则项实现这一目标。

---